14 Elementos de álgebra matricial

Objetivos del capítulo

Al finalizar este capítulo, el lector estará en capacidad de:

• Explicar en sus propias palabras los conceptos de: matriz, suma y multiplicación de matrices, matriz identidad, transpuesta de una matriz e inversa de una matriz.
• Calcula en R la suma y multiplicación de matrices, la matriz identidad, la transpuesta de una matriz y la inversa de una matriz.

14.1 Introducción

Este libro supone el conocimiento básico de álgebra matricial que le permiten al científico de datos trabajar con grandes volúmenes de datos organizados en forma matricial. Este Apéndice presenta dichos elementos necesarios para seguir algunas demostraciones y operaciones descritas en el libro. Este Apéndice no pretende ser un tratado autocontenido de álgebra matricial, sino por el contrario un breve resumen que permitirá al lector ya familiarizado con el álgebra matricial recordar los concepto¹³⁴.

El concepto de matrices es una noción que inicialmente se desarrolló en el siglo XVII, para la manipulación de gráficos y soluciones de ecuaciones lineales simultáneas. Hoy en día la aplicación de las matrices y sus operaciones están ligadas a áreas tan diversas como la física, gráficos de computador, la economía, los métodos estadísticos, la teoría de juegos, redes, criptología y la ciencia de datos.

Una matriz es una forma eficiente de ordenar información en columnas y filas. Por ejemplo, consideremos una base de datos que contiene información de ventas, costos y utilidades mensuales para dos empresas (empresa 1 y 2) en millones de dólares. La información de un mes se puede ordenar fácilmente en una matriz de la siguiente forma: \[\begin{equation} M=\begin{bmatrix} Empresa & Ventas& Costos& Utilidades \\ Empresa 1 & 4 & 2 & 2\\ Empresa 2 & 2 & 1.5 & 0.5 \end{bmatrix} \tag{14.1} \end{equation}\] Generalmente, se omiten los nombres que toman cada una de las columnas y filas de las matrices; es decir, (14.1) se puede reescribir como: \[\begin{equation*} M=\begin{bmatrix} 4 & 2 & 2\\ 2 & 1.5 & 0.5 \end{bmatrix} \end{equation*}\]

El tamaño de una matriz está determinado por el número de filas y de columnas; así, se dice que la matriz \(M\) es una matriz de dimensiones \(2 \times 3\) (2 filas por 3 columnas). Una forma rápida de escribir esto es \(M_{2 \times 3}\). En general una matriz puede tener \(n\) filas y \(m\) columnas, y se representa así: \[\begin{equation*} A_{n \times m}=\begin{bmatrix} a_{11} & \dots & a_{1m}\\ \vdots & \ddots & \vdots \\ a_{n1} & \dots & a_{nm} \end{bmatrix} =\left [ a_{ij} \right ]_{i=1, \dots, n;j=1, \dots, m} \end{equation*}\]

En el caso especial cuando \(m=1\), la matriz \(A\) se conoce como un vector columna. Si \(n=1\), la matriz \(A\) se conoce como un vector fila. Cuando el número de filas y de columnas es el mismo (\(n=m\)), la matriz \(A\) es llamada matriz cuadrada de orden \(n\). Si \(n=m=1\), entonces \(A\) es conocido como un escalar (lo que coloquialmente se conoce como un número).

En el caso de las matrices, se dice que \(A=B\) si y solamente si todos los elementos de la matriz \(A\) son iguales a los de \(B\), es decir \(a_{ij} = b_{ij}\) para todo \(i\) y \(j\), donde \(i=1, \dots, n\) y \(j=1, \dots, m\).

A continuación, repasaremos rápidamente las operaciones matriciales, definiciones y resultados más importantes que serán útiles a lo largo del libro.

14.2 Matriz triangular y diagonal

Antes de definir algunas matrices especiales que serán útiles, es importante definir el concepto de diagonal principal de una matriz. La diagonal principal de una matriz cuadrada \(A\), es el conjunto de elementos cuya posición corresponden a la misma fila y columna. En otras palabras, son los elementos que se encuentran formando una “diagonal” entre la esquina superior izquierda y la esquina inferior derecha de la matriz. Por ejemplo, sea la matriz: \[\begin{equation*} C=\begin{bmatrix} 1 & 2 & 4\\ 6 & 3 & 5 \\ 11 & 10 & 8 \end{bmatrix} \end{equation*}\] La diagonal principal de la matriz \(C\) está dada por el conjunto \({1,3,8}\).

En general, sea \(A\) una matriz cuadrada representada por: \[\begin{equation} A_{n \times m}=\begin{bmatrix} a_{11} & \dots & a_{1n}\\ \vdots & \ddots & \vdots \\ a_{n1} & \dots & a_{nn} \end{bmatrix} =\left [ a_{ij} \right ]_{i=1, \dots, n;j=1, \dots, n} \tag{14.2} \end{equation}\] Entonces, la diagonal principal está dada por el conjunto de elementos \(\left \{ a_{ii} \right \}_{i=1, \dots, n}\).

Por otro lado, una matriz triangular superior (inferior) es una matriz cuadrada con todos los elementos por debajo (encima) de la diagonal principal iguales a cero. Por ejemplo, la siguiente matriz: \[\begin{equation*} \begin{bmatrix} 1 & 2 & 4\\ 0 & 3 & 5 \\ 0 & 0 & 8 \end{bmatrix} \end{equation*}\] es una matriz triangular superior.

Si una matriz es al mismo tiempo una matriz triangular superior y triangular inferior, entonces se conoce como una matriz diagonal. En otras palabras, una matriz diagonal es una matriz cuyos elementos por fuera de la diagonal principal son cero. Es decir, \(A\) es una matriz diagonal si tiene la siguiente forma: \[\begin{equation*} \begin{bmatrix} a_{11} & 0 & 0\\ 0 & \ddots & 0 \\ 0 & 0 & a_{nn} \end{bmatrix} \end{equation*}\]

Una matriz diagonal se puede escribir de forma corta de la siguiente manera \(A = diag\left ( a_{11}, a_{22}, \dots, a_{nn} \right )\).

14.3 Adición, multiplicación por un escalar y multiplicación de matrices

Sean dos matrices \(A\) y \(B\), cada una de dimensiones \(n \times m\). Es decir, las dos matrices tienen el mismo número de filas y columnas, cuando ocurre esto se le denomina a las dos matrices conformes para la suma. La suma de estas dos matrices corresponde a una matriz con dimensiones \(n \times m\), cuyos elementos son iguales a la suma de los elementos correspondientes de las matrices \(A\) y \(B\) . En otras palabras: \[\begin{equation*} \begin{aligned} A+B & = \begin{bmatrix} a_{11} & \dots & a_{1m}\\ \vdots & \ddots & \vdots \\ a_{n1} & \dots & a_{nm} \end{bmatrix}+ \begin{bmatrix} b_{11} & \dots & b_{1m}\\ \vdots & \ddots & \vdots \\ b_{n1} & \dots & b_{nm} \end{bmatrix} \\ &= \begin{bmatrix} a_{11}+b_{11} & \dots &a_{1m}+ b_{1m}\\ \vdots & \ddots & \vdots \\ a_{n1} + b_{n1} & \dots & a_{nm}b_{nm} \end{bmatrix} \\ &=\left [ a_{ij} + b_{ij} \right ]_{i=1, \dots, n;j=1, \dots, m} \end{aligned} \end{equation*}\] Si las matrices a sumar no tienen las mismas dimensiones, entonces la operación no se puede efectuar y se dice que las matrices no cumplen la condición de conformidad.

Ejemplo: Suma de matrices

Suponga que contamos con 3 matrices que corresponden a la información para los tres primeros meses del año de las ventas, costos y utilidades mensuales (columnas) para dos empresas (filas).

\[\begin{equation*} E=\begin{bmatrix} 600 & 250 & 350\\ 550 & 180 & 400 \end{bmatrix} \: \: F=\begin{bmatrix} 650 & 330 & 250\\ 600 & 270 & 400 \end{bmatrix} \: \:M=\begin{bmatrix} 580 & 270 & 350\\ 6250 & 350 & 410 \end{bmatrix} \end{equation*}\]

Encuentre el valor de las ventas, costos y utilidades para el primer trimestre.

Respuesta: Las ventas, costos y utilidades trimestrales para las dos empresas son: \[\begin{equation*} E+F+M=\begin{bmatrix} 1830 & 850 & 950\\ 1775 & 800 & 1210 \end{bmatrix} \end{equation*}\].

La suma de matrices posee varias propiedades similares a las de la suma de escalares. A continuación se exponen estas propiedades:

• Propiedad Conmutativa: \(A+B = B+A\)
• Propiedad Asociativa: \(A+B+C= (A+B) +C = A+(B+C)\)

Antes de avanzar un poco más, note que si se suma dos veces la matriz \(A\), se obtiene:

\[\begin{equation*} \begin{aligned} A+A & =\begin{bmatrix} a_{11} & \dots & a_{1n}\\ \vdots & \ddots & \vdots \\ a_{n1} & \dots & a_{nn} \end{bmatrix}+\begin{bmatrix} a_{11} & \dots & a_{1n}\\ \vdots & \ddots & \vdots \\ a_{n1} & \dots & a_{nn} \end{bmatrix}\\ &=\begin{bmatrix} 2a_{11} & \dots & 2a_{1n}\\ \vdots & \ddots & \vdots \\ 2a_{n1} & \dots & 2a_{nn} \end{bmatrix} = 2 \begin{bmatrix} a_{11} & \dots & a_{1n}\\ \vdots & \ddots & \vdots \\ a_{n1} & \dots & a_{nn} \end{bmatrix}\\ &= 2 \cdot \left [ a_{ij} \right ]_{i=1, \dots, n;j=1, \dots, n} = 2 \cdot A \end{aligned} \end{equation*}\]

Es decir, el resultado de sumar dos veces la matriz \(A\) es igual a cada uno de los elementos de la matriz \(A\) multiplicado por dos. Así es fácil mostrar que en general: \[\begin{equation*} \lambda \cdot A =\begin{bmatrix} \lambda a_{11} & \dots & \lambda a_{1n}\\ \vdots & \ddots & \vdots \\ \lambda a_{n1} & \dots & \lambda a_{nn} \end{bmatrix} \end{equation*}\] donde \(\lambda\) es un escalar.

Ejemplo: (continuación)

Suponga que quiere calcular \(E-F+2M\).

Respuesta: Tenemos que: \[\begin{equation*} E-F+2M = E + (-1)F + 2M \end{equation*}\] Por lo tanto, \[\begin{equation*} E-F+2M = \begin{bmatrix} 600 & 250 & 350\\ 550 & 180 & 400 \end{bmatrix} + \begin{bmatrix} -650 & -330 & -250\\ -600 & -270 & -400 \end{bmatrix} + \begin{bmatrix} 2 \cdot 580 & 2 \cdot 270 & 2 \cdot 350\\ 2 \cdot 6250 & 2 \cdot 350 & 2 \cdot 410 \end{bmatrix} \end{equation*}\]

Y por lo tanto \[\begin{equation*} E-F+2M = \begin{bmatrix} 1110 & 460 & 800\\ 1200 & 610 & 820 \end{bmatrix} \end{equation*}\]

Finalmente, consideremos la multiplicación de dos matrices. En este caso, a diferencia de la multiplicación entre escalares, las matrices a multiplicar deben cumplir una condición de conformidad para que el producto exista. Esta condición es que el número de columnas de la primera matriz debe ser igual al número de filas de la segunda matriz. Es decir, dadas dos matrices \(A\) y \(B\) con dimensiones \(n_A \times m_A\) y \(n_B \times m_B\), respectivamente; el producto \(A \cdot B\) cumple la condición de conformidad si y solamente si \(m_A = n_B\). En caso de que esta condición se cumpla, el producto estará dado por: \[\begin{equation} A \cdot B = \left [ c_{ij} \right ]_{i=1, \dots, n;j=1, \dots, n} \tag{14.3} \end{equation}\] donde, \(c_{ij}=\sum_{l=1}^{m}{a_{il} \cdot b_{il}}\). La Figura 14.1¹³⁵ ilustra el uso de esta fórmula. Cada una de las parejas unidas por las líneas rojas se multiplican entre sí. Posteriormente, se suman dichos productos para obtener el correspondiente elemento de la matriz final \(C\).

Figura 14.1: Diagrama de multiplicación de matrices

Fuente: este diagrama es una modificación del encontrado en https://texample.net/tikz/examples/matrix-multiplication/.

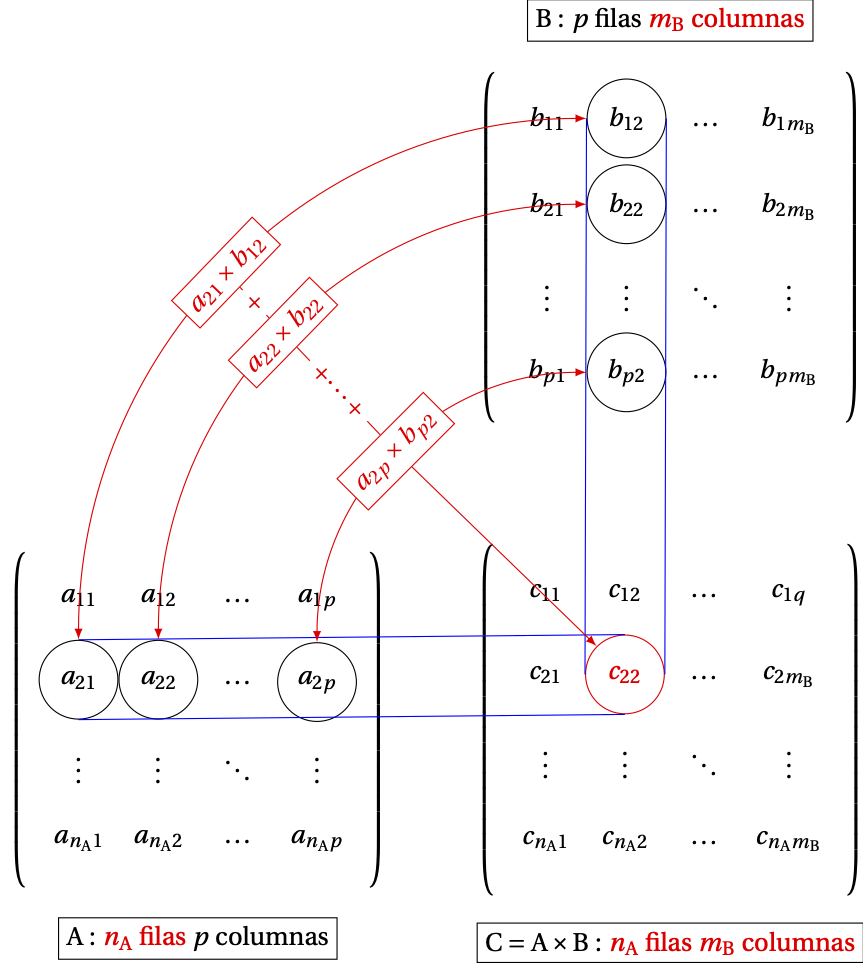
La multiplicación de matrices presenta varias propiedades, pero antes es importante recalcar que la propiedad conmutativa de la multiplicación para los escalares no se cumple para las matrices (aún si este producto cumple la condición de conformidad). Es decir, \(A \cdot B \neq B \cdot A\) en caso de que ambos productos estén definidos. Por esto, es importante tener en cuenta el orden en que se multiplican las matrices, y hablaremos de pre-multiplica o post-multiplicar por una matriz, cuando se multiplica una matriz por la izquierda o por la derecha, respectivamente.

Las siguientes son las propiedades que se cumplen para la multiplicación de matrices:

• Propiedad Asociativa: \(A \cdot B \cdot C = \left ( A \cdot B \right )\cdot C = A \cdot \left ( B \cdot C \right )\)
• Propiedad Distributiva: \(C\left ( A + B \right )= \left ( C \cdot A \right ) + \left ( C \cdot B \right )=C \cdot A + C \cdot B\) y \(\left ( A + B \right )C= A \cdot C + B \cdot C\).

Un caso especial se presenta cuando consideramos una matriz diagonal. Sea \(A\) una matriz diagonal de orden \(n\), entonces tenemos que \(A \cdot A = A^2 = \left [ a_{ij}^2 \right ]_{i=1, \dots, n;j=1, \dots, n}\). Por ejemplo, si: \[\begin{equation*} A = \begin{bmatrix} 4 & 0\\ 0 & 6 \end{bmatrix}, \end{equation*}\] tendremos que:

\[\begin{equation*} A \cdot A = A^2 = \begin{bmatrix} 16 & 0\\ 0 & 36 \end{bmatrix}. \end{equation*}\]

En general, si \(A\) es una matriz diagonal de orden \(n\), tendremos que \(A^\alpha = \left [ a_{ij}^\alpha \right ]_{i=1, \dots, n;j=1, \dots, n}\). Es decir, cuando se eleva una matriz diagonal a la \(\alpha\), el resultado es una matriz diagonal, cuyos elementos en la diagonal principal son iguales a los correspondientes elementos de la diagonal principal de la matriz original elevados cada uno a la \(\alpha\).

Ejemplo: Multiplicación de matrices

Dadas las siguientes dos matrices \(A \cdot A = \begin{bmatrix} 1 & 2\\ 4 & 3\\ 1 & 6 \end{bmatrix}\) y \(B = \begin{bmatrix} 1 & 2 & 1\\ 2 & 4 & 1 \end{bmatrix}\), encuentre \(A \cdot B\).

Respuesta: Inicialmente, es importante chequear que se cumpla la condición de conformidad. En este caso el número de columnas de la matriz \(A\) es igual al número de filas de la matriz \(B\). Así, el producto \(A \cdot B\) está definido: las matrices son conformables. Procedamos a encontrar dicho producto. \[\begin{equation*} A \cdot B = \begin{bmatrix} 1 & 2\\ 4 & 3\\ 1 & 6 \end{bmatrix} \cdot \begin{bmatrix} 1 & 2 & 1\\ 2 & 4 & 1 \end{bmatrix}. \end{equation*}\] Y por tanto, \[\begin{equation*} A \cdot B = \begin{bmatrix} (1 \cdot 1) + (2 \cdot 2) & (1 \cdot 2) + (2 \cdot 4) & (1 \cdot 1) + (2 \cdot 1)\\ (4\cdot 1) + (3 \cdot 2) & (4 \cdot 2) + (3 \cdot 4) & (4 \cdot 1) + (3 \cdot 1)\\ (1 \cdot 1) + (6 \cdot 2) & (1 \cdot 2) + (6 \cdot 4) & (1 \cdot 1) + (6 \cdot 1) \end{bmatrix} . \end{equation*}\]

Esto implica que \[\begin{equation*} A \cdot B = \begin{bmatrix} 5 & 10 & 3\\ 10 & 20 & 7\\ 13 & 26 & 7 \end{bmatrix} . \end{equation*}\] Finalmente, noten que \(B \cdot A\) también está definido. Realiza ésta última multiplicación.

Es importante anotar que las matrices, así como los escalares, pueden ser sumadas, restadas o multiplicadas (siempre y cuando el producto esté definido). Pero la división para las matrices no es posible.

Si consideramos dos números (escalares) \(a\) y \(b\) , entonces el cociente \(\frac{a}{b}\) (siempre y cuando \(b \neq 0\)) se puede expresar como \(ab^{-1}=b^{-1}a\), donde \(b^{-1}\) se conoce como el recíproco o inverso de \(b\). Debido a la propiedad conmutativa de la multiplicación de escalares, la expresión \(\frac{a}{b}\) se puede emplear sin ningún problema para expresar \(ab^{-1}\) o \(b^{-1}a\).

En el caso de las matrices esto es diferente. Debe ser claro, que aunque los productos \(AB^{-1}\) y \(B^{-1}A\) estén definidos¹³⁶, estos dos productos usualmente son diferentes. De manera que, la expresión \(\frac{A}{B}\) no puede emplearse porque es ambigua. Es decir, no es claro si esta expresión se refiere a \(AB^{-1}\) o \(B^{-1}A\). Y peor aún, es posible que alguno de estos productos no exista. Así, cuando manipulamos matrices, es mejor evitar el uso de la expresión \(\frac{A}{B}\) (matriz \(A\) dividida por la matriz \(B\)) (Chiang, 1996).

14.4 La matriz identidad y la matriz de ceros.

La matriz identidad es una matriz diagonal especial, cuyos elementos de la diagonal principal son iguales a uno. Es decir, la matriz identidad es una matriz con unos en la diagonal principal y ceros en las otras posiciones. La matriz identidad se denota por \(I_n\), donde \(n\) corresponde al número de columnas y filas de la matriz (orden de la matriz). Formalmente, \[\begin{equation} I_n=\begin{bmatrix} 1 & &0 \\ & \ddots & \\ 0 & &1 \end{bmatrix} \tag{14.4} \end{equation}\]

La matriz identidad tiene la propiedad de ser el módulo de la multiplicación de matrices. Es decir, \(I_k \cdot A_{k \times g} = A\) y \(A_{k \times g} \cdot I_g= A\).

Un caso especial se produce cuando \(A_{k \times g} \cdot I_g= I_g\), donde tiene que ser cierto que \(A_{k \times g} =I_g\). ¿Por qué? (asegúrese que puede encontrar el por qué de esta afirmación).

Otra matriz importante es la matriz de ceros, cuyos elementos son iguales a cero y se denota por \(0_{n \times m}\). Esta matriz no necesariamente debe ser cuadrada y tiene la siguiente propiedad: \(A_{n \times m} + 0_{n \times m} = 0_{n \times m} + A_{n \times m} = A\). Es decir, \(0_{n \times m}\) es el módulo de la suma (siempre que la suma sea conformable).

14.5 La transpuesta de una matriz y la matriz simétrica.

La transpuesta de una matriz cualquiera \(A\) es una matriz cuyas filas corresponden a las columnas de la matriz original; o lo que es lo mismo, es una matriz cuyas columnas corresponden a las filas de la matriz \(A\). La transpuesta de una matriz \(A\) se denota por \(A^T\) o \({A}'\).

Por ejemplo, la transpuesta de: \[\begin{equation*} C = \begin{bmatrix} 1 & 2 & 4\\ 6 & 3 & 5\\ 11 & 10 & 8 \end{bmatrix} \end{equation*}\] es; \[\begin{equation*} C^T = \begin{bmatrix} 1 & 6 & 11\\ 2 & 3 & 10\\ 4 & 5 & 8 \end{bmatrix}. \end{equation*}\]

Las propiedades de la operación de transposición son las siguientes:

• Transpuesta de la transpuesta: \(\left ( A^T \right )^T=A\)
• Transpuesta de una suma: \(\left ( A + B \right )^T=A^T + B^T\)
• Transpuesta de un producto: \(\left ( A \cdot B \right )^T=B^T \cdot A^T\)

Cuando \(A^T = A\), se dice que \(A\) es una matriz simétrica. En otras palabras, una matriz simétrica es una matriz cuya transpuesta es igual a ella misma. Por ejemplo, la siguiente matiz es simétrica: \[\begin{equation*} D = \begin{bmatrix} 1 & 2 & 4\\ 6 & 3 & 5\\ 4 & 5 & 8 \end{bmatrix} \end{equation*}\] Dado que, \[\begin{equation*} D^T = \begin{bmatrix} 1 & 2 & 4\\ 6 & 3 & 5\\ 4 & 5 & 8 \end{bmatrix} = D \end{equation*}\]

Generalmente, por convención, las matrices simétricas son escritas omitiendo los elementos por debajo de la diagonal principal. Para nuestro ejemplo tendremos que la matriz \(D\) se puede reescribir de la siguiente forma: \[\begin{equation*} D = \begin{bmatrix} 1 & 2 & 4\\ & 3 & 5\\ & & 8 \end{bmatrix} \end{equation*}\]

Cuando se emplea esta notación se da por entendido que se trata de una matriz simétrica.

14.6 Matriz idempotente y matrices ortogonales

Una matriz cuadrada \(A\) se denomina idempotente si y solamente si \(A \cdot A = A\). Un ejemplo de matriz idempotente es la matriz identidad. Por otro lado, dos matrices \(A\) y \(B\) son matrices ortogonales si y solamente si \(A \cdot B = 0\) .

14.7 Combinaciones lineales de vectores e independencia lineal

Dado un conjunto de vectores (fila o columna) \(v_1, v_2, \dots, v_k\) y un conjunto de escalares \(\alpha_1, \alpha_2, \dots, \alpha_k\) para \(k = 1, 2, \dots, K\), una combinación lineal de los vectores está dada por \[\begin{equation} c=\sum_{i=1}^{K}{\alpha_i v_i} \tag{14.5} \end{equation}\]

Ejemplo: Combinaciones lineal de vectores

Dados los siguientes 3 vectores y 3 escalares, encuentre 4 diferentes combinaciones lineales de los vectores.

\[\begin{equation*} v=\begin{bmatrix} 2\\ 3\\ 5\\ 6 \end{bmatrix},\:w=\begin{bmatrix} 4\\ 6\\ 1\\ 0 \end{bmatrix},\:z=\begin{bmatrix} 5\\ 10\\ 0\\ 1 \end{bmatrix},\:\alpha=2,\: \beta=1,\:\gamma=-1. \end{equation*}\]

Respuesta: A partir de estos vectores y escalares podemos encontrar las siguientes combinaciones lineales: \[\begin{equation*} c_1=\alpha v+ \beta w+\gamma z=2\begin{bmatrix} 2\\ 3\\ 5\\ 6 \end{bmatrix} +1 \begin{bmatrix} 4\\ 6\\ 1\\ 0 \end{bmatrix}+(-1) \begin{bmatrix} 5\\ 10\\ 0\\ 1 \end{bmatrix}= \begin{bmatrix} 3\\ 2\\ 11\\ 11 \end{bmatrix} \end{equation*}\]

\[\begin{equation*} c_2= \beta v+\alpha w+\gamma z=1\begin{bmatrix} 2\\ 3\\ 5\\ 6 \end{bmatrix} +2 \begin{bmatrix} 4\\ 6\\ 1\\ 0 \end{bmatrix}+(-1) \begin{bmatrix} 5\\ 10\\ 0\\ 1 \end{bmatrix}= \begin{bmatrix} 5\\ 5\\ 7\\ 5 \end{bmatrix} \end{equation*}\]

\[\begin{equation*} c_3= \beta v+\gamma w+ \alpha z=1\begin{bmatrix} 2\\ 3\\ 5\\ 6 \end{bmatrix} +(-1) \begin{bmatrix} 4\\ 6\\ 1\\ 0 \end{bmatrix}+2 \begin{bmatrix} 5\\ 10\\ 0\\ 1 \end{bmatrix}= \begin{bmatrix} 11\\ 19\\ -3\\ -5 \end{bmatrix} \end{equation*}\]

\[\begin{equation*} c_4= \gamma v+ \beta w+ \alpha z=(-1)\begin{bmatrix} 2\\ 3\\ 5\\ 6 \end{bmatrix} + 1 \begin{bmatrix} 4\\ 6\\ 1\\ 0 \end{bmatrix}+2 \begin{bmatrix} 5\\ 10\\ 0\\ 1 \end{bmatrix}= \begin{bmatrix} 12\\ 23\\ -4\\ -4 \end{bmatrix} \end{equation*}\]

Ahora tenemos todos los elementos para definir el concepto de dependencia lineal. Un conjunto de vectores será linealmente dependiente si al menos uno de los vectores puede expresarse como una combinación lineal de los otros. Así por ejemplo, el conjunto de vectores \(c, v_1, v_2, \dots, v_k\) (definidos anteriormente), será dependiente linealmente, pues por definición el vector \(c\) es una combinación lineal de los demás vectores (\(c=\sum_{i=1}^{K}{\alpha_i v_i}\)).

Ahora bien, un conjunto de vectores \(v_1, v_2, \dots, v_k\) se considera linealmente independiente si y solamente si los únicos valores de los escalares \(\alpha_1, \alpha_2, \dots, \alpha_k\) que cumplen la condición: \[\begin{equation} \sum_{i=1}^{K}{\alpha_i v_i} = 0 \tag{14.6} \end{equation}\] son \(\alpha_1 = \alpha_2 = \dot =\alpha_k = 0\). En otras palabras, ningún vector del conjunto se puede expresar como combinación lineal de otro u otros vectores que pertenecen al mismo conjunto.

14.8 La Traza y el rango de una matriz

La traza de una matriz cuadrada \(A\) es la suma de los elementos de la diagonal principal y se denota por \(tr(A)\). Es decir: \[\begin{equation} tr(A_{n \times n})=\sum_{i=1}^{n}{a_{ii}} \tag{14.7} \end{equation}\]

Una de las principales propiedades de la traza es: \(tr(A \cdot B \cdot C) = tr(C \cdot B \cdot A) = tr(B \cdot C \cdot A) =\).

Por otro lado, el rango de una matriz \(A\) es el número de filas o columnas linealmente independientes y se denota por \(ran(A)\). Si se trata de una matriz no simétrica de dimensiones \(n \times m\), entonces tendremos que \(ran(A)\leq \min(n,m)\).

Si el rango de una matriz \(A\) es igual al número de sus columnas, entonces se dice que la matriz \(A\) tiene rango columna completo. En caso de que el rango de la matriz \(A\) sea igual al número de filas, se dice que la matriz \(A\) tiene rango fila completo. Para el caso de una matriz cuadrada, si el rango de la matriz es igual al número de filas y por tanto al número de columnas, se dice que la matriz tiene rango completo.

Ejemplo: Rango de una matriz

Encuentre el rango de la siguiente matriz: \[\begin{equation*} D= \begin{bmatrix} 2 & 4 & 5 & 12\\ 3 & 6 & 10 & 23\\ 5 & 1 & 0 & -4\\ 6 & 0 & 1 & -4 \end{bmatrix}. \end{equation*}\] Respuesta: Noten que esta matriz se construye con los vectores columna \(v\), \(w\), \(z\) y \(c_4\) del ejemplo anterior. Es más recuerden que \(c_4= \gamma v+ \beta w+ \alpha z\). Es decir, la última columna (vector columna) se puede construir como una combinación lineal de las primeras tres columnas. Además se puede comprobar rápidamente que las tres primeras filas son linealmente independientes entre sí. Así, \(ran(D) = 3\).

Algunos resultados útiles del rango son:

• \(ran(A \cdot B)= \min(ran(A), ran(B))\)
• Si \(A\) tiene dimensiones \(n \times m\) y \(B\) es una matriz cuadrada de rango \(m\), entonces \(ran(AB) = ran(A)\)
• \(ran(A) = ran (A^T A) = ran(AA^T)\)

14.9 Determinante de una matriz

El determinante de una matriz cuadrada \(A\), representado por \(det(A)\) o \(\left | A \right |\), es un escalar asociado de manera unívoca con esta matriz. Para una matriz \(2 \times 2\), el determinante está dado por: \[\begin{equation} det(A)=\left | A \right |= \left | \begin{bmatrix} a_{11}& a_{12} \\ a_{21} & a_{22} \end{bmatrix} \right |=a_{11}a_{22}-a_{21}a_{12} \tag{14.8} \end{equation}\] Para una matriz de un orden superior, el cálculo del determinante es un poco más complejo.

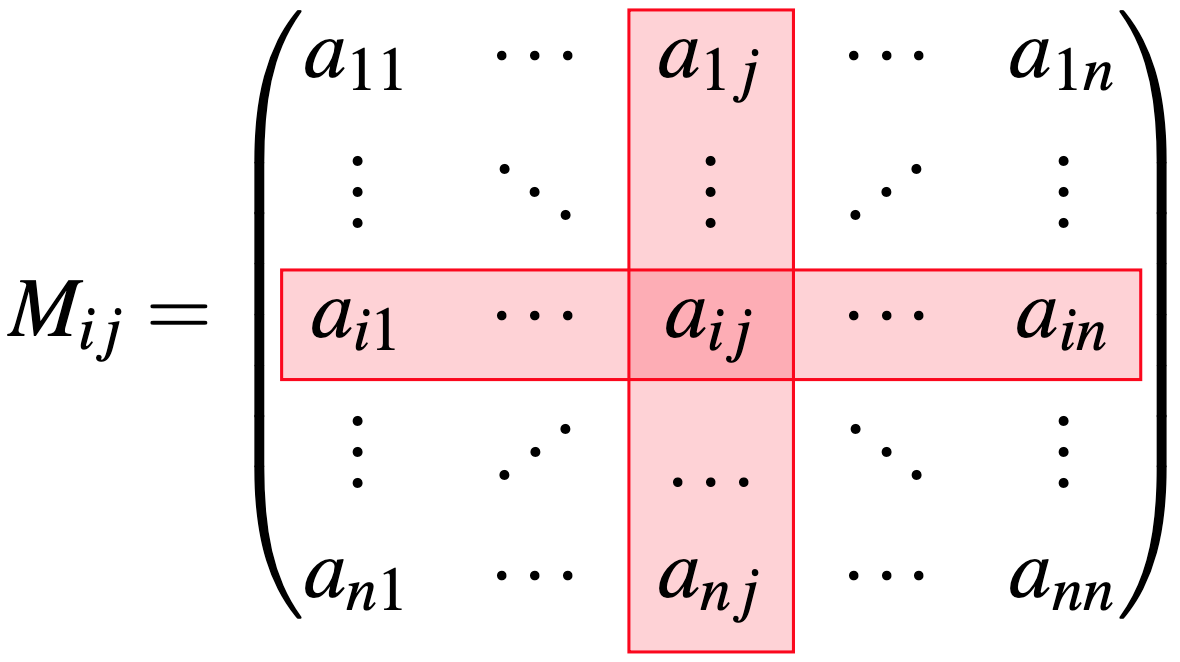
Antes de entrar en el detalle del cálculo, definamos dos conceptos importantes. La matriz menor, asociada al elemento \(a_{ij}\) de una matriz cuadrada \(A\) de orden \(n\), denotada por \(M_{ij}\), es la matriz cuadrada de orden \(n-1\) obtenida al eliminar la i-ésima fila y la j-ésima columna de \(A\). (Ver Figura 14.2). El menor del elemento \(a_{ij}\) es el determinante de la matriz menor \(M_{ij}\); es decir, \(\left | M_{ij} \right |\). Y el cofactor del elemento \(a_{ij}\), expresado por \(C_{ij}\), corresponde a \(C_{ij}= (-1)^{i+j} \left | M_{ij} \right |\) (Ver columna y fila sombreadas en rojo en la Figura 14.2).

Figura 14.2: Diagrama de la matriz menor asociada al elemento \(a_{ij}\) de la matriz \(A\)

Fuente: elaboración propia.

Ahora bien, el determinante de una matriz de orden \(n\) puede ser calculado, a partir de cualquier columna o fila, de la siguiente manera:

• empleando la i-ésima fila: \(det(A)=\left | A \right |= \sum_{j=1}^{n}{a_{ij}}C_{ij}\)
• empleando la j-ésima columna: \(det(A)=\left | A \right |= \sum_{i=1}^{n}{a_{ij}}C_{ij}\)

Algunas propiedades útiles del determinante son:

• \(det(A) = det(A^T)\)
• \(\left | A^T \right | = \left | A \right |\)
• \(\left | A \cdot \right | = \left | A \right | \cdot \left | B \right |\)
• Si el producto de una fila de \(A\) por un escalar se suma a una fila de \(A\), entonces el determinante de la matriz resultante es igual al \(\left | A \cdot \right |\)
• El intercambio de dos filas o dos columnas, sin importar cuales sean, alterará el signo, pero no el valor numérico, del determinante.
• \(det(\lambda A_n) = \lambda^n det(A)\), donde \(\lambda\) es un escalar.
• \(det(A) = 0\) si y solamente si \(ran(A) < n\). Es decir, si \(det(A) = 0\), entonces tiene que ser cierto que existe una columna (o fila) que es combinación lineal de una, o más de una columna (fila), de \(A\).
• Si \(det(A) = 0\), entonces \(A\) se conoce como una matriz singular. En caso contrario (i.e. \(det(A) \neq 0\)) se dice que \(A\) es una matriz no singular.
• Si \(A\) es una matriz diagonal denotada por \(A =diag(a_{11},a_{22}, \dots, a_{nn}), entonces det(A) =a_{11}\cdot a_{22}\cdot \dots \cdot a_{nn}\).

Ejemplo: Cálculo del determinante de una matriz

Encuentre el determinante de la siguiente matriz: \[\begin{equation*} D= \begin{bmatrix} 2 & -1 & 3 & 5\\ 2 & 0 & 1 & 0\\ 6 & 1 & 3 & 4\\ -7 & 3 & -2 & 8 \end{bmatrix} \end{equation*}\] Respuesta: El determinante puede ser calculado empleando cualquier fila o columna, en este caso será más fácil emplear la segunda fila, pues tiene dos elementos iguales a cero. Así, tendremos: \[\begin{equation*} \left | D \right | = \left | \begin{bmatrix} 2 & -1 & 3 & 5\\ 2 & 0 & 1 & 0\\ 6 & 1 & 3 & 4\\ -7 & 3 & -2 & 8 \end{bmatrix} \right | = 2\cdot (-1)^{2+1} \left | \begin{bmatrix} -1 & 3 & 5\\ 1 & 3 & 4\\ 3 & -2 & 8 \end{bmatrix} \right | + 1\cdot (-1)^{2+3} \left | \begin{bmatrix} 2 & -1 & 5\\ 6 & 1 & 4\\ -7 & 3 & 8 \end{bmatrix} \right | \end{equation*}\]

Note que esto implicará el cálculo de dos determinantes de orden 3. Esta operación se puede simplificar aún más si “creamos” más ceros en la segunda fila de la matriz \(D\). Por ejemplo, si multiplicamos la columna 3 por -2 y sumamos este producto a la columna 1 tendremos que: \[\begin{equation*} \left | D \right | = \left | \begin{bmatrix} 2 & -1 & 3 & 5\\ 2 & 0 & 1 & 0\\ 6 & 1 & 3 & 4\\ -7 & 3 & -2 & 8 \end{bmatrix} \right | = \left | \begin{bmatrix} -4 & -1 & 3 & 5\\ 0 & 0 & 1 & 0\\ 0 & 1 & 3 & 4\\ -3 & 3 & -2 & 8 \end{bmatrix} \right | = 1\cdot (-1)^{2+3} \left | \begin{bmatrix} -4 & -1 & 5\\ 0 & 1 & 4\\ -3 & 3 & 8 \end{bmatrix} \right | \end{equation*}\] Ahora, multiplicando la segunda columna por -4 y sumándola a la tercera columna se obtendrá: \[\begin{equation*} \begin{aligned} \left | D \right | & = -1 \left | \begin{bmatrix} -4 & -1 & 5\\ 0 & 1 & 4\\ -3 & 3 & 8 \end{bmatrix} \right | = -1 \left | \begin{bmatrix} -4 & -1 & 9\\ 0 & 1 & 0\\ -3 & 3 & -4 \end{bmatrix} \right | = -1(-1)^{2+2}\left | \begin{bmatrix} -4 & 9\\ -3 & -4 \end{bmatrix} \right | \\ & =-1(1)\left [ (-4)(-4)- (-3)(9) \right ]\\ &=-\left [ 16 + 27\right ]= -43. \end{aligned} \end{equation*}\]

14.10 Valores propios de una matriz

Los valores propios (eigen values en inglés), también conocidos como raíces características de una matriz cuadrada \(A_n\) son los escalares \(\lambda\) que satisfacen: \[\begin{equation} \left | A-\lambda In \right | = 0 \tag{14.9} \end{equation}\] Es decir, para encontrar los valores propios se debe resolver la anterior ecuación.

Los valores propios son importantes porque en muchos casos facilitan ciertos cálculos. En especial tenemos los siguientes resultados:

• \(det(A_n)=\prod_{i=1}^{n}{\lambda_i}\).
• El rango de cualquier matriz \(A\) es igual al número de valores propios diferentes de cero.

Ejemplo: Valores propios de una matriz

Encuentre los valores propios, rango y determinante de la siguiente matriz: \[\begin{equation*} D= \begin{bmatrix} 5 & 1\\ 2 & 4 \end{bmatrix} \end{equation*}\] Respuesta: Para encontrar los valores propios de la matriz \(D\), se requiere solucionar la siguiente ecuación \(\left | D-\lambda In \right | = 0\). Es decir,

\[\begin{equation*} \left | \begin{bmatrix} 5 & 1\\ 2 & 4 \end{bmatrix} - \lambda I_2 \right |=0 \end{equation*}\]

\[\begin{equation*} \left | \begin{bmatrix} 5 & 1\\ 2 & 4 \end{bmatrix} - \lambda \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} \right |=0 \end{equation*}\]

\[\begin{equation*} \left | \begin{bmatrix} 5-\lambda & 1\\ 2 & 4-\lambda \end{bmatrix} \right |=0 \end{equation*}\]

\[\begin{equation*} (5-\lambda)(4-\lambda)-2(1)=0 \end{equation*}\] \[\begin{equation*} \lambda^2-9 \lambda+18=0 \end{equation*}\]

Las dos soluciones son \(\lambda_1 = 6\) ó \(\lambda_2 = 3\). Así, los valores propios de la matriz \(D\) son 6 y 3. Por tanto, \(ran(D)=2\) y \(det(D) = 6 \cdot 3 = 18\).

14.11 La Matriz inversa

La matriz inversa de la matriz cuadrada \(A_n\) es una matriz cuadrada de igual orden tal que: \[\begin{equation} B \cdot A_n = I_n \tag{14.10} \end{equation}\] Y se denota como \(A^{-1}\), es decir \(B=A^{-1}\). Además, si se post-multiplica la matriz \(A_n\) por su inversa, también se obtendrá la matriz identidad. En otras palabras, la matriz inversa además cumple que \(A_n A_n^{-1}= I_n\).

Pero, ¿cómo encontrar la matriz inversa de una matriz \(A_n\) ? Primero es importante recordar que no todas las matrices cuadradas poseen inversa. De hecho, sólo aquellas matrices cuyas columnas y filas son linealmente independientes entre sí tendrán inversa. En otras palabras, una matriz singular (\(det(A)=0\)) no tendrá matriz inversa.

Existen diferentes métodos para encontrar la matriz inversa de una matriz no singular, pero aquí sólo repasaremos dos métodos. El primer método será emplear la transpuesta de la matriz de cofactores conocida como la matriz adjunta (\(Adj(A)\)). La matriz inversa de una matriz \(A_n\) está dada por la siguiente fórmula: \[\begin{equation} A_n^{-1}=\frac{1}{\left | An \right |}Adj(A_n) \tag{14.11} \end{equation}\]

Figura 14.3: Ejemplo de una matriz adjunta de orden tres

Fuente: elaboración propia.

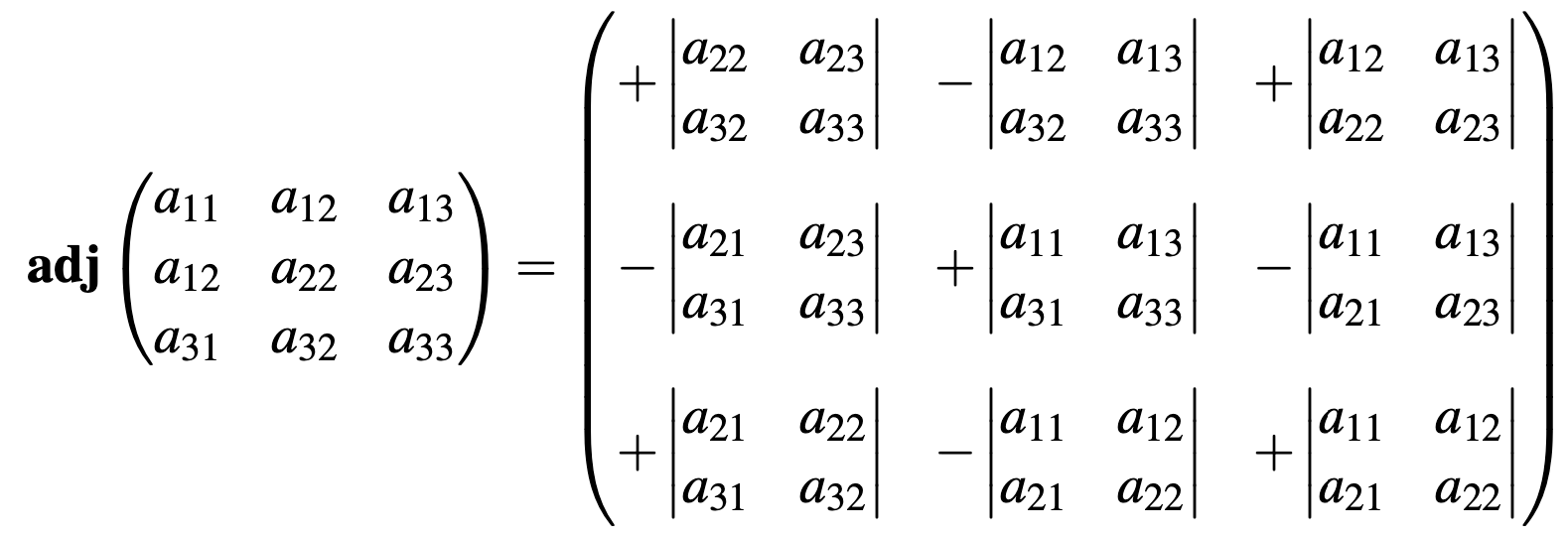
Ejemplo: Cálculo de la inversa empleando el método de la matriz adjunta

Encuentre la inversa de la siguiente matriz \[\begin{equation*} D= \begin{bmatrix} 3 & 2 \\ 1 & 0 \\ \end{bmatrix}. \end{equation*}\] Respuesta: Para emplear la fórmula que se presenta en ((14.11)), primero debemos calcular tanto el determinante como la matriz adjunta de \(D\). Así, tenemos que \(det(D) = -2\) y \(Adj(D)=\begin{bmatrix} 0 & -2\\ -1& 3 \end{bmatrix}\)

Aplicando la fórmula, la inversa de \(D\) esta dada por \[\begin{equation*} D^{1}=- \frac{1}{2} \begin{bmatrix} 0 & -2\\ -1& 3 \end{bmatrix} =\begin{bmatrix} 0 & -1\\ \frac{1}{2}& -\frac{3}{2} \end{bmatrix}. \end{equation*}\] Ahora, constate que en efecto esta si es la inversa de \(D\).

El segundo método que consideraremos es el método de reducción de Gauss-Jordan. En algunas ocasiones, este método resulta menos tedioso que aplicar la fórmula dada en (14.11). Dada una matriz cuadrada \(A_n\), este método parte de considerar la siguiente matriz aumentada:

\[\begin{equation} \left [ \left.\begin{matrix} a_{11} & \dots & a_{1n}\\ \vdots & \ddots & \vdots \\ a_{n1} & \dots & a_{nn} \end{matrix}\right| \begin{matrix} 1 & & 0\\ & \ddots & \\ 0 & & 1 \end{matrix}\right ]=\left [ \left. A_n \right| I_n \right ] \tag{14.12} \end{equation}\]

Posteriormente, por medio de operaciones de filas podemos reducir la matriz \(A\) a la matriz identidad. Así tendremos que: \[\begin{equation} \left [ \left. \begin{matrix} 1 & & 0\\ & \ddots & \\ 0 & & 1 \end{matrix}\right| \begin{matrix} d_{11} & \dots & d_{1n}\\ \vdots & \ddots & \vdots \\ d_{n1} & \dots & d_{nn} \end{matrix} \right ]=\left [ \left. I_n \right| A_n \right ]. \tag{14.13} \end{equation}\] Al final de las transformaciones, obtendremos la inversa de la matriz original a la derecha.

Ejemplo: Calculo de la inversa empleando el método de reducción de Gauss-Jordan

Encuentre la inversa de la siguiente matriz empleando el método de reducción de Gauss-Jordan \[\begin{equation*} E= \begin{bmatrix} 2 & 9 \\ 1 & 4 \\ \end{bmatrix} \end{equation*}\] Respuesta: Primero necesitamos armar la matriz aumentada. Es decir: \[\begin{equation*} \left [ \left.\begin{matrix} 2 & 9\\ 1 & 4 \end{matrix}\right| \begin{matrix} 1 & 0\\ 0 & 1 \end{matrix}\right ] \end{equation*}\] Ahora necesitamos manipular esta matriz de tal forma que a la izquierda tengamos la matriz inversa. Para esto, intercambiemos la primera fila con la segunda. \[\begin{equation*} \left [ \left.\begin{matrix} 1 & 4\\ 2 & 9\\ \end{matrix}\right| \begin{matrix} 0 & 1\\ 1 & 0 \end{matrix}\right ] \end{equation*}\]

Posteriormente, sumemos la fila uno multiplicada por (-2) a la fila 2. \[\begin{equation*} \left [ \left.\begin{matrix} 1 & 4\\ 0 & 1 \end{matrix}\right| \begin{matrix} 0 & 1\\ 1 & -2 \end{matrix}\right ] \end{equation*}\] Finalmente, sumemos la fila 2 multiplicada por (-4) a la fila 1. \[\begin{equation*} \left [ \left.\begin{matrix} 1 & 0\\ 0 & 1 \end{matrix}\right| \begin{matrix} -4 & 9\\ 1 & -2 \end{matrix}\right ] \end{equation*}\]

Por tanto, \[\begin{equation*} D^{-1}=\begin{bmatrix} -4 & 9\\ 1 & -2 \end{bmatrix}. \end{equation*}\]

Un resultado especial, que es muy útil, es la inversa de una matriz diagonal. Ésta es una de las inversas más fáciles de calcular. En general tenemos que: \[\begin{equation} \begin{bmatrix} a_{11} & & 0\\ & \ddots & \\ 0 & & a_{nn} \end{bmatrix}^{-1}=\begin{bmatrix} \frac{1}{a_{11}} & & 0\\ & \ddots & \\ 0 & & \frac{1}{a_{nn}} \end{bmatrix} \tag{14.14} \end{equation}\]

Finalmente, repasemos rápidamente algunas propiedades de las matrices inversas:

• \((AB)^{-1} = B^{-1}A^{-1}\)
  • \((A^{-1})^{-1}= A\)
  • \((A^{T})^{-1}=(A^{-1})^{T}\)
  • Si \(A\) es una matriz simétrica, entonces \(A^{-1}\) también será simétrica

14.12 Elementos de cálculo matricial

Consideremos la siguiente función cuyo dominio es en los reales (\(\mathbb{R}X\)) y su rango pertenece a \(\mathbb{R}^n:y=f\left ( x_1, x_2, \dots, x_n \right )=f\left ( \mathbf{x}\right )\). El vector de derivadas parciales de \(f\left ( \mathbf{x}\right )\) es conocido como el gradiente o vector gradiente y está definido de la siguiente manera: \[\begin{equation} g=g\left ( \mathbf{x}\right )=\frac{\partial f\left ( \mathbf{x}\right )}{\partial \mathbf{x}}=\begin{bmatrix} \partial y/ \partial x_1\\ \partial y/ \partial x_2\\ \vdots\\ \partial y/ \partial x_n\\ \end{bmatrix}=\begin{bmatrix} f_1\\ f_2\\ \vdots\\ f_n\\ \end{bmatrix} \tag{14.15} \end{equation}\]

Es importante tener en cuenta que el gradiente es un vector columna y no un vector fila.

El elemento i-ésimo del gradiente se interpreta como la pendiente de \(f\left ( \mathbf{x}\right )\) con respecto al plano formado por \(x_i\) y \(y\); en otras palabras, es el cambio en \(f\left ( \mathbf{x}\right )\) dado un cambio en \(x_i\) teniendo los otros elementos del vector \(\mathbf{x}\) constantes.

La segunda derivada de \(f\left ( \mathbf{x}\right )\) está dada por una matriz denominada la matriz Hessiana que es calculada de la siguiente manera: \[\begin{equation} \begin{aligned} H&=\begin{bmatrix} \partial^2 y/ \partial x_1\partial x_1 & \partial^2 y/ \partial x_1\partial x_2 & \dots & \partial^2 y/ \partial x_1\partial x_n\\ \partial^2 y/ \partial x_2\partial x_1 & \partial^2 y/ \partial x_2\partial x_2 & \dots & \partial^2 y/ \partial x_2\partial x_n\\ \vdots & \vdots & \vdots &\vdots \\ \partial^2 y/ \partial x_n\partial x_1 & \partial^2 y/ \partial x_n\partial x_2 & \dots & \partial^2 y/ \partial x_n\partial x_n\\ \end{bmatrix}\\ &=\left [ f_{ij} \right ] = \frac{ \partial^2 y}{\partial \mathbf{x}\partial \mathbf{x}^T} \end{aligned} \tag{14.16} \end{equation}\] La matriz Hessiana es cuadrada y simétrica, gracias al Teorema de Young.

Algunas derivadas especiales útiles para la construcción de modelos de regresión múltiple son:

• \(\frac{ \partial\left ( \mathbf{x}^T \mathbf{a} \right )}{\partial \mathbf{x}}=\mathbf{a}\), donde \(\mathbf{a}\) es un vector columna
• \(\frac{ \partial\left ( \mathbf{x}^T A \mathbf{x}\right )}{\partial \mathbf{x}}=\left ( A+A^T \right )\mathbf{x}\), donde \(A\) es cualquier matriz cuadrada
• \(\frac{ \partial\left ( \mathbf{x}^T A \mathbf{x}\right )}{\partial \mathbf{x}}=2A\mathbf{x}\), donde \(A\) es una matriz cuadrada simétrica.

Ahora si consideramos funciones cuyo rango está en los \(\mathbb{R}^n\), tenemos los siguientes resultados que son de gran utilidad:

• \(\frac{ \partial\left ( A \mathbf{x}\right )}{\partial \mathbf{x}}=A^T\), donde \(A\) es cualquier matriz tal que el producto \(A \mathbf{x}\) está definido.
• \(\frac{ \partial\left ( \mathbf{x}^T A \mathbf{x}\right )}{\partial \mathbf{x}}=\mathbf{x}^T\mathbf{x}\), donde \(A\) es cualquier matriz cuadrada.
• \(\frac{ ln(A)}{\partial A}=(A^{-1})^T\), donde \(A\) es cualquier matriz cuadrada no-singular.

14.13 Resultados especiales para el modelo de regresión múltiple

Antes de finalizar, es importante resaltar varios resultados importantes que serán empleados en este libro. Los datos de una muestra se organizarán en un vector columna \(y_{n \times 1}\) que contendrá los datos de las \(n\) observaciones para la variable dependiente. \[\begin{equation} y_{n \times 1} =\begin{bmatrix} y_1\\ y_2\\ \vdots\\ y_n \end{bmatrix} \tag{14.17} \end{equation}\] Y una matriz \(X_{n \times k}\) que contiene las variables explicativas y una columna de unos para el intercepto. \[\begin{equation} X_{n \times k} =\begin{bmatrix} 1 & X_{21}& X_{31}& \dots & X_{k1}\\ 1 & X_{22}& X_{32}& \dots & X_{k2}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & X_{n2}& X_{3n}& \dots & X_{kn} \end{bmatrix} \tag{14.18} \end{equation}\] Noten que en este contexto hemos cambiado un poco la notación de las filas y las columnas. El primer número corresponde al número de la variable y el segundo a la observación \(i\) (fila). Es decir, \(X_{32}\) corresponde a la segunda observación de la variable \(X_2\).

Usando estas definiciones, tendremos los siguientes resultados:

\[\begin{equation} X^TX=\begin{bmatrix} n & \sum_{i=1}^{n}{X_{2i}}& \sum_{i=1}^{n}{X_{3i}}& \dots &\sum_{i=1}^{n}{X_{ki}}\\ & \sum_{i=1}^{n}{X_{2i}^2}& \sum_{i=1}^{n}{X_{2i}X_{3i}}& \dots & \sum_{i=1}^{n}{X_{2i}X_{ki}}\\ & & \sum_{i=1}^{n}{X_{3i}^2} & \ddots & \sum_{i=1}^{n}{X_{3i}X_{ki}} \\ & & & \ddots & \vdots \\ & & & & \sum_{i=1}^{n}{X_{ki}^2} \end{bmatrix}_{k \times k} \tag{14.19} \end{equation}\]

Adicionalmente, \[\begin{equation} y^Ty=\sum_{i=1}^{n}{y_{i}^2} \tag{14.20} \end{equation}\]

Finalmente, tenemos que \[\begin{equation} X^Ty=\begin{bmatrix} \sum_{i=1}^{n}{y_{i}}\\ \sum_{i=1}^{n}{y_i X_{2i}^2}\\ \sum_{i=1}^{n}{y_i X_{3i}^2}\\ \vdots \\ \sum_{i=1}^{n}{y_i X_{ki}^2}\\ \end{bmatrix}_{k \times 1} \tag{14.21} \end{equation}\]

Ejemplo: Matrices en la criptología

Como se mencionó al inicio de este capítulo, una de las aplicaciones de las matrices es la criptología; es decir, el proceso de cifrar mensajes. A continuación veremos una breve aplicación de las matrices a la codificación de mensajes.

Considere una matriz fija \(A\) invertible (no singular). Entonces, podemos convertir el mensaje que se desea codificar en una matriz \(B\) , tal que \(A \times B\) satisfaga la condición de conformidad. Así, se puede enviar el mensaje generado por el producto \(A \times B\). El receptor del mensaje necesita conocer solamente \(A^{-1}\) para decodificar el mensaje. Esto gracias a que \(A^{-1}A B = B\).

Para entender cómo funciona esto, consideremos la siguiente matriz \[\begin{equation*} A= \begin{bmatrix} -1 & 5 & -1 \\ -2 & 11 & 7 \\ 1 & -5 & 2 \end{bmatrix} \end{equation*}\] La correspondiente inversa es \[\begin{equation*} A^{-1}= \begin{bmatrix} 57 & -5 & 46 \\ 11 & -1 & 9 \\ -1 & 0 & -1 \end{bmatrix} \end{equation*}\] Ahora supongamos que queremos transmitir el mensaje “Estamos en Cali”. Para esto necesitamos crear una equivalencia entre las letras y un número. Por ejemplo supongamos que se crea la siguiente equivalencia: \(e = 3\), \(s = 4\), \(t = 5\), \(a = 1\), \(m = 6\), $o = 8 $, \(n = 7\), \(c = -1\), \(l = 9\), \(i = -2\) y para los espacios en blanco usaremos el cero.

\[\begin{equation*} \begin{bmatrix} 3 & 4 & 5 & 1 & 6 \\ 8 & 4 & 0 & 3 & 7 \\ 0 & -1 & 1 & 9 & -2 \\ \end{bmatrix} \end{equation*}\] Esto se puede expresar de la siguiente manera (note que el receptor del mensaje también debe conocer la codificación adecuada de las letras). Así, podemos crear la siguiente matriz \[\begin{equation*} B= \begin{bmatrix} 3 & 4 & 5 & 1& 6 \\ 8 & 4 & 0 &3 & 7 \\ 0 &-1 & 1& 9 &-2 \end{bmatrix} \end{equation*}\]

Entonces tenemos que \[\begin{equation*} AB= \begin{bmatrix} 37 & 17 & -6 & 5 & 31 \\ 82 & 29 & -3 &94 & 51 \\ -37 &-18 & 7& 4 &-33 \end{bmatrix} \end{equation*}\] Por tanto, el mensaje encriptado a enviar sería: {37,17,37, 17 , -6 , 5, 31, 82, \(\dots\)}. El receptor puede saber cuántas filas tendrá la matriz que le es enviada al conocer \(A\). Y podrá fácilmente reconstruir la matriz \(AB\). De tal forma que pre-multiplicando por \(A^{-1}\) el mensaje recibido se obtendrá el mensaje deseado.

Ejercicio: Encripte el mensaje “Tengo que repasar álgebra matricial”.

14.14 Empleando R para hacer operaciones matriciales

R Core Team (2023) es un lenguaje de programación que emplea vectorización. Es decir, la forma natural de hacer cálculos en R es emplear vectores y matrices y no escalares. Esto hace el lenguaje matricial sea un lenguaje natural al momento de emplear R.

Empecemos por crear la siguiente matriz \[\begin{equation*} D= \begin{bmatrix} 2 & -1 & 3 & 5\\ 2 & 0 & 1 & 0\\ 6 & 1 & 3 & 4\\ -7 & 3 & -2 & 8 \end{bmatrix}. \end{equation*}\]

Es se puede hacer con la función matrix() del paquete base de R. Esta función requiere los siguientes argumentos: matrix(data = NA, nrow = 1, ncol = 1, byrow = FALSE)

donde:

• data: los datos que estarán en la matriz.
• nrow: número de filas.
• ncol: número de columnas.
• byrow: Valor lógico. Si byrow = FALSE (el valor por defecto) la matriz se llena por columnas, de lo contrario la matriz se llena por filas.

La matriz \(D\) se puede construir rápidamente empleando el código que se observa a continuación.

  D <- matrix(c(2, -1, 3, 5, 2, 0, 1, 0,6, 1, 3, 4, -7, 3, -2, 8), nrow = 4, ncol = 4, byrow = TRUE )
D

##      [,1] [,2] [,3] [,4]
## [1,]    2   -1    3    5
## [2,]    2    0    1    0
## [3,]    6    1    3    4
## [4,]   -7    3   -2    8

class(D)

## [1] "matrix" "array"

Por otro lado, una matriz identidad puede ser construida rápidamente con la función diag(). Para crear una matriz identidad de orden \(n\) el único atributo que requiere la función es el tamaño de la matriz identidad (\(n\)). Es decir,

  diag(4)

##      [,1] [,2] [,3] [,4]
## [1,]    1    0    0    0
## [2,]    0    1    0    0
## [3,]    0    0    1    0
## [4,]    0    0    0    1

La misma función diag() permite extraer los valores de la diagonal principal de una matriz, si el argumento de esta es una función.

  diag(D)

## [1] 2 0 3 8

Así, la traza de la matriz \(D\) se puede calcular de la siguiente manera:

  sum(diag(D))

## [1] 13

Por otro lado, si queremos sumar matrices, esto se puede hacer rápidamente empleando el operados +. Por ejemplo, supongamos que queremos sumarle a la matriz \(D\) la siguiente matriz \[\begin{equation*} E= \begin{bmatrix} 3 & 3 & 7 & 51\\ 4 & 9 & 1 & 3\\ 5 & 10 & 3 & 12\\ 8 & 21 & -2 & 4 \end{bmatrix} \end{equation*}\]

  E <- matrix(c(3, 3, 7, 51, 4, 9, 1, 3, 5, 10, 3, 12, 8, 21, -2, 4), nrow = 4, ncol = 4, byrow = TRUE )
E

##      [,1] [,2] [,3] [,4]
## [1,]    3    3    7   51
## [2,]    4    9    1    3
## [3,]    5   10    3   12
## [4,]    8   21   -2    4

D + E

##      [,1] [,2] [,3] [,4]
## [1,]    5    2   10   56
## [2,]    6    9    2    3
## [3,]   11   11    6   16
## [4,]    1   24   -4   12

Para la multiplicación de matrices se debe tener un poco de cuidado. El operador \* realiza una multiplicación elemento por elemento, no realiza la multiplicación de las matrices. Por otro lado el operador “%*%” si realiza la multiplicación de matrices. Es decir:

  #multiplicación elemento por elemento
  D * E

##      [,1] [,2] [,3] [,4]
## [1,]    6   -3   21  255
## [2,]    8    0    1    0
## [3,]   30   10    9   48
## [4,]  -56   63    4   32

#multiplicación de matrices
D %*% E

##      [,1] [,2] [,3] [,4]
## [1,]   57  132   12  155
## [2,]   11   16   17  114
## [3,]   69  141   44  361
## [4,]   45  154  -68 -340

El determinante de una matriz, y sus valores propios se pueden calcular empleando las funciones det() y eigen() , respectivamente. Por ejemplo:

  #determinante
  det(D)

## [1] -43

#valores propios
eigen(D)

## eigen() decomposition
## $values
## [1]  6.851893+5.934594i  6.851893-5.934594i -1.156348+0.000000i
## [4]  0.452562+0.000000i
## 
## $vectors
##                       [,1]                  [,2]           [,3]          [,4]
## [1,] -0.0919841+0.4433032i -0.0919841-0.4433032i -0.47221621+0i -0.2400156+0i
## [2,]  0.0983345+0.1285593i  0.0983345-0.1285593i  0.07723466+0i  0.5743704+0i
## [3,]  0.0947980+0.5778436i  0.0947980-0.5778436i  0.85512230+0i  0.7399695+0i
## [4,] -0.6526363+0.0000000i -0.6526363+0.0000000i -0.19953074+0i -0.2548258+0i

eigen(D)$values

## [1]  6.851893+5.934594i  6.851893-5.934594i -1.156348+0.000000i
## [4]  0.452562+0.000000i

Finalmente, la matriz inversa se puede encontrar con la función solve() .

  #Inversa
  solve(D)

##             [,1]      [,2]       [,3]        [,4]
## [1,] -0.09302326 -1.744186  0.5348837 -0.20930233
## [2,] -0.27906977  2.767442 -0.3953488  0.37209302
## [3,]  0.18604651  4.488372 -1.0697674  0.41860465
## [4,]  0.06976744 -1.441860  0.3488372 -0.09302326

#chequeo
round(solve(D)%*%D, 3)

##      [,1] [,2] [,3] [,4]
## [1,]    1    0    0    0
## [2,]    0    1    0    0
## [3,]    0    0    1    0
## [4,]    0    0    0    1

Referencias

Alonso, J. C. (2006b). Apuntes de álgebra matricial para un curso introductorio de econometrı́a. Apuntes de Economı́a; No. 11-2006.

Chiang, A. (1996). Métodos fundamentales de economı́a. Madrid: McGraw-Hill.

R Core Team. (2023). R: A language and environment for statistical computing. R Foundation for Statistical Computing. https://www.R-project.org/

---

134. Este apéndice corresponde a una versión adaptada de Alonso (2006b).↩︎

135. Esta representación se conoce como el esquema de Falk.↩︎

136. \(B^{-1}\) denota la inversa de la matriz \(B\) en caso de que exista. Este concepto será repasado más adelante.↩︎