1 Introducción
Objetivos del capítulo
Al finalizar este capítulo, el lector estará en capacidad de:
- Explicar en sus propias palabras las diferentes tareas de analítica
- Explicar en sus propias palabras los tipos de analítica
- Explicar en sus propias palabras las diferencias entre la aproximación econométrica tradicional y la de análisis de los científicos de datos
Los modelos de analítica y la disponibilidad de grandes volúmenes de información están transformando el mundo de los negocios y la forma como las organizaciones generan valor para sus grupos de interés. La gran cantidad de datos disponibles genera grandes oportunidades para emplear herramientas de business analytics y Big Data que permitan tanto optimizar los procesos actuales de la organización, como generar características diferenciadoras que acompañen los nuevos productos que lanza la organización.
Los datos se han convertido en un recurso muy importante para las organizaciones, y el business analytics se ha convertido en la forma cómo las organizaciones pueden monetizar ese recurso. El business analytics es el proceso científico de transformar datos en insights con el propósito de tomar mejores decisiones. En últimas, el business analytics empodera a la organización para el logro de su misión.
En ese proceso científico de transformar datos en conclusiones con el propósito de tomar mejores decisiones existen diferentes actividades que van desde la recolección de datos y su almacenamiento hasta la toma de la decisión; pasando por la extracción, limpieza y preparación de los datos, su exploración y visualización y el modelado o experimentación o predicción o lo que sea que requiera para responder la pregunta de negocio planteada. Estas actividades no son desarrolladas por una sola persona. Normalmente existe un equipo con profesionales calificados que tienen diferentes competencias y roles en este proceso. En estos equipos está como nodo central el científico de datos quien estima y entrena modelos estadísticos y de inteligencia artificial o diseña experimentos para resolver las preguntas de negocio planteadas.
Figura 1.1: Material multimedia: roles en la analítica

El científico de datos exitoso necesita tener en su caja de herramientas diferentes aproximaciones estadísticas y de inteligencia artificial para poder emplear la herramienta adecuada para responder determinada pregunta de negocio. Este libro se centra en la tarea de regresión (que se explicará más adelante) y en una herramienta estadística muy potente y flexible: el modelo clásico de regresión múltiple.
Antes de entrar en materia con el modelo clásico de regresión, en este capítulo estudiaremos las diferentes tareas de la analítica, los tipos de analítica y la diferencia entre la aproximación tradicional de las ciencias y la ciencia de datos al momento de usar el modelo de regresión.
1.1 Tareas del científico de datos
El científico de datos en sus labores cotidianas se encuentra siempre en la necesidad de escoger la mejor herramienta para responder la pregunta de negocio planteada. Las respuestas a las preguntas de negocio implican diferentes tareas que se pueden clasificar en uno o varios de los siguientes tipos:
- Resumir
- Visualizar
- Clusterizar (Agrupar)
- Clasificar
- Detectar excepciones
- Asociar
- Estimar regresiones
- Pronosticar
Resumir implica simplificar la representación de los datos para generar información. La tareas de Visualizar facilita la comprensión y el descubrimiento de los datos por medio de gráficos. El clústering parte de una muestra para encontrar grupos de elementos similares. Por ejemplo, en la Figura 1.2 se presenta un conjunto de clientes que por medio de un modelo de clústering es distribuido en dos grupos de acuerdo con ciertas características.
Figura 1.2: Tarea de clústering
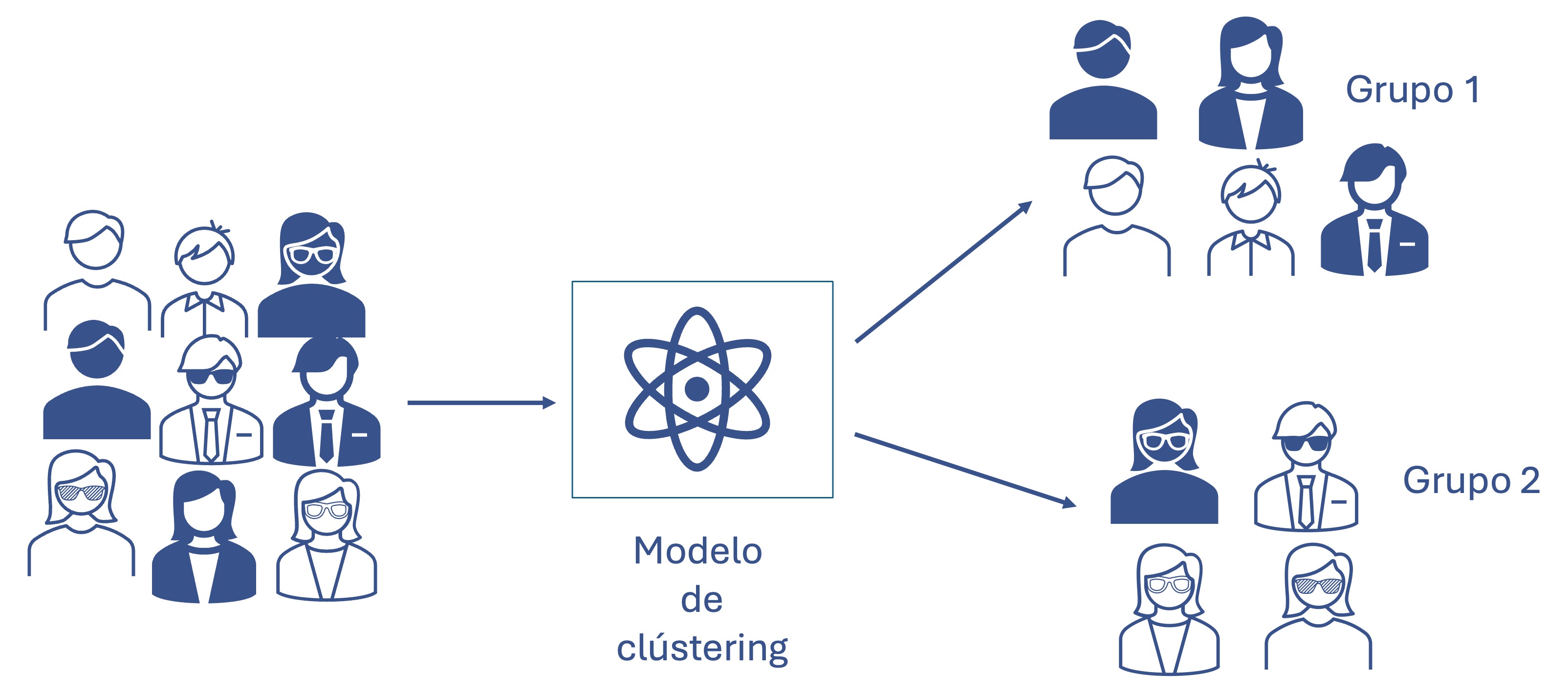
Para realizar las diferentes tareas de analítica empleamos modelos o algoritmos5. En el ejemplo de la Figura 1.2 el modelo de clústering encuentra dos grupos: los que tienen gafas y los que no. Este tipo de modelo no tiene una variable a explicar e implica que el modelo o algoritmo aprenda sobre la estructura de los datos. A este tipo de algoritmos se les conoce como modelos de aprendizaje no supervisado.
Figura 1.3: Material multimedia: tarea de clústering

La tarea de Clasificación tiene como finalidad predecir la categoría de un individuo. Por ejemplo, en algunas situaciones se deseará determinar si un nuevo cliente comprará o no nuestro producto. En este caso las categorías son compra o no compra. Otro tipo de preguntas que puede resolver esta tarea son: ¿se irá el cliente?, ¿pagará el crédito? y ¿será el individuo un buen match para la posición? En la Figura 1.4 se presenta una representación gráfica de esta tarea. Para esta tarea se emplean modelos o algoritmos que se estiman6 empleando una muestra de individuos para los cuáles se tiene información de sus características y una variable dependiente que recoge si el individuo pertenece o no a una categoría. En este orden de ideas, los modelos que se emplean para esta tarea son modelos que intentan entender la relación entre unas variables y una variable categórica; relación que ya ocurrió en algún periodo. Este tipo de modelos se les conoce como algoritmos de aprendizaje supervisado, pues al modelo se le debe “enseñar” a que categoría pertenece cada individuo.
Figura 1.4: Tarea de clasificación
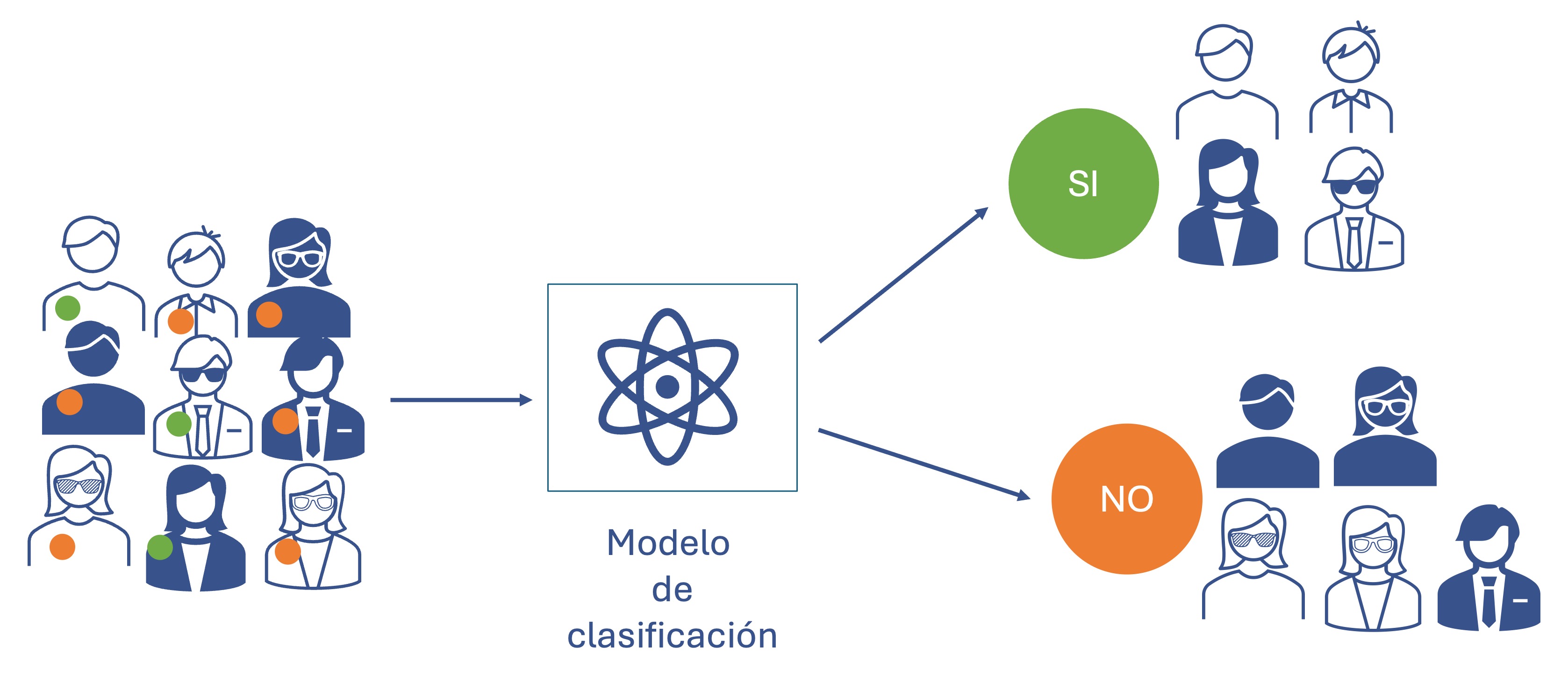
Figura 1.5: Material multimedia: tarea de clasificación

La tarea de Detección de excepciones tiene como objetivo encontrar individuos con características o comportamiento diferentes. Esta tarea emplea modelos de aprendizaje no supervisado. La tarea de encontrar Asociaciones busca reglas de co-ocurrencia de productos en diferentes canastas. Es decir, busca encontrar cuáles productos son comprados regularmente al mismo tiempo que otros para poder sugerir composición de canastas. Estos modelos intentan encontrar la estructura de los datos sin la necesidad de enseñarle al algoritmo cuáles son las co-ocurrencias. Estos son modelos de aprendizaje no supervisado.
La tarea de Estimar regresiones implica encontrar relaciones entre muchas variables y una variable cuantitativa de interés. Esto puede ser tanto para entender qué variables están asociadas a un fenómeno, como para simular el comportamiento en diferentes escenarios. En la Figura 1.6 se presenta un ejemplo en el que se tienen las características de diferentes clientes y variables como el gasto en publicidad (estas son las variables independientes) y el precio y el modelo de regresión determina la relación de estas variables con el monto (en dinero) de las compras (variable dependiente). Estos modelos son considerados modelos de aprendizaje supervisado.
Figura 1.6: Tarea de regresión

La tarea de Estimar regresiones se puede desarrollar empleando algoritmos de inteligencia artificial o modelos estadísticos. Los modelos estadísticos empleados para la estimación de las relaciones entre una variable dependiente y una o más variables independientes pueden ser clasificados en dos grandes categorías: los lineales y los no lineales. Los modelos de regresión que asumen una relación lineal entre las variables independientes y la dependiente corresponden al modelo clásico de regresión múltiple. Este tipo de modelo, aunque a primera vista parecería muy restrictivo el supuesto del comportamiento lineal, puede ser muy flexible como lo veremos a lo largo de este libro.
Finalmente, la tarea de generar Pronósticos implica predecir el comportamiento futuro de una variable cuantitativa7. Para esta tarea se emplean los patrones de comportamiento pasados para extrapolarlas al futuro. Estos modelos son considerados modelos de aprendizaje supervisado.
Este libro se concentra en el modelo Clásico de Regresión Múltiple que permite realizar la tarea de Estimar regresiones y en algunos casos la tarea de Pronosticar si se emplea un componente temporal en el modelo. Este modelo fue desarrollado por la estadística, y los economistas han popularizado su uso para variables económicas y del mundo de los negocios dando origen a una disciplina conocida como la econometría. En este orden de ideas, en este libro nos concentramos en este modelo econométrico. Estas herramientas de la econometría constituyen hoy un pilar importante de la caja de herramientas de los científicos de datos. En la sección 1.3 se discute la diferencia entre la aproximación de la econometría a resolver problemas empleando el modelo clásico de regresión múltiple y la ciencia de datos.
1.2 Tipos de analítica
Antes de continuar es importante recordar que existen cuatro tipos de analítica: descriptiva, diagnóstica, predictiva y prescriptiva. (Ver Figura 1.8). Estos tipos de analítica engloban las tareas que discutimos anteriormente. No necesariamente un tipo de analítica es mejor que otra, cada una cumple una función diferente y responde a preguntas diferentes. Pero, es claro que a medida que pasamos de la analítica descriptiva a la prescriptiva se genera mayor valor a las organizaciones, al tiempo que se está aumentando el grado de complejidad.
Figura 1.7: Material multimedia: tipos de analítica

Figura 1.8: Tipos de analítica

La analítica descriptiva responde a la pregunta ¿qué está pasando en mi negocio? Para esto emplea las bases de datos de la compañía, o las disponibles públicamente8 y emplea la estadística descriptiva para explorar los datos, resumir información en reportes y visualizaciones que sean útiles para entender qué ha pasado y qué está pasando con el negocio. Este tipo de analítica es la más utilizada en las empresas y es la que requiere menor grado de sofisticación técnica para aplicarlas.
La analítica diagnóstica típicamente quiere responder la pregunta de por qué está pasando lo que está pasando en el negocio. Este tipo de análisis tiene la capacidad de encontrar las causas de los problemas, la raíz de las relaciones y es capaz de aislar los efectos de diferentes fenómenos. El modelo de regresión que estudiaremos en este documento permite encontrar relaciones y aislar efectos.
La analítica predictiva busca responder la pregunta: ¿qué es posible que ocurra? Para esto se apoya en datos históricos; es decir, con los datos que ya se tiene, se predicen comportamientos que aún no se conocen. En otras palabras, con datos ya existentes se predicen los datos que aún no se tienen o no han ocurrido. La predicción implica estimar los resultados de los datos no vistos. La creación de pronósticos (forecasting en inglés) es un área de la predicción en la que se realizan conjeturas sobre el futuro, basándonos en datos de series de tiempo9. La única diferencia entre la predicción y los pronósticos es que en esta última se considera la dimensión temporal. La analítica predictiva tiene como intención generar predicciones de variables cuantitativas.
El modelo de regresión múltiple puede emplearse tanto para hacer predicciones como pronósticos. Por ejemplo, si se emplea una muestra de muchos individuos en el mismo periodo (muestra de corte trasversal) para encontrar las variables asociadas a la cantidad de unidades que compra un cliente, el modelo podría ser empleado para responder la pregunta ¿cuánto compraría un nuevo cliente con determinadas características? En el Capítulo 12 se discutirá el uso del modelo de regresión múltiple para hacer predicciones. Si el modelo de regresión múltiple es estimado con series de tiempo (se observa uno o varios objetos de estudio periodo tras periodo), entonces podrá ser empleado para hacer pronósticos. Por ejemplo, si se cuenta con las ventas mensuales para muchos periodos y el modelo encuentra que variables están asociadas a estas ventas mes tras mes, el modelo podría responder la pregunta que ocurrirá en el futuro con las ventas. Con este tipo de modelos podemos responder preguntas como: ¿cuánto es lo más probable que venda un producto el próximo año?
Finalmente, la analítica prescriptiva busca responder la pregunta: ¿qué necesito hacer?. Este tipo de analítica hace énfasis en el uso de técnicas de optimización para identificar cuál es la mejor alternativa para minimizar o maximizar algún objetivo, así como modelos que permitan simular situaciones. El modelo de regresión múltiple pueden hacer parte de un análisis prescriptivo como se discutirá más adelante.
1.3 Aproximación econométrica vs los científicos de datos
La econometría es una disciplina que unifica las matemáticas, la estadística y la teoría económica con el objetivo de entender cuantitativamente las relaciones económicas (Frisch, 1933). Ésta ha desarrollado unas técnicas estadísticas que le han permitido convertirse en una rama de la estadística. Si bien las técnicas que estudiaremos en este libro no son exclusivas de la econometría, la aplicación del modelo de regresión múltiple a problemas de los negocios y la economía se conoce como una aproximación econométrica. Pero hay que tener cuidado y distinguir claramente las herramientas de la econometría y la aproximación econométrica a los problemas, pues como científico de datos emplearemos las herramientas de la econometría pero no la aproximación econométrica para hacer validar los modelos teóricos de la ciencia económica.
Figura 1.9: Ruta metodológica tradicional de la econometría
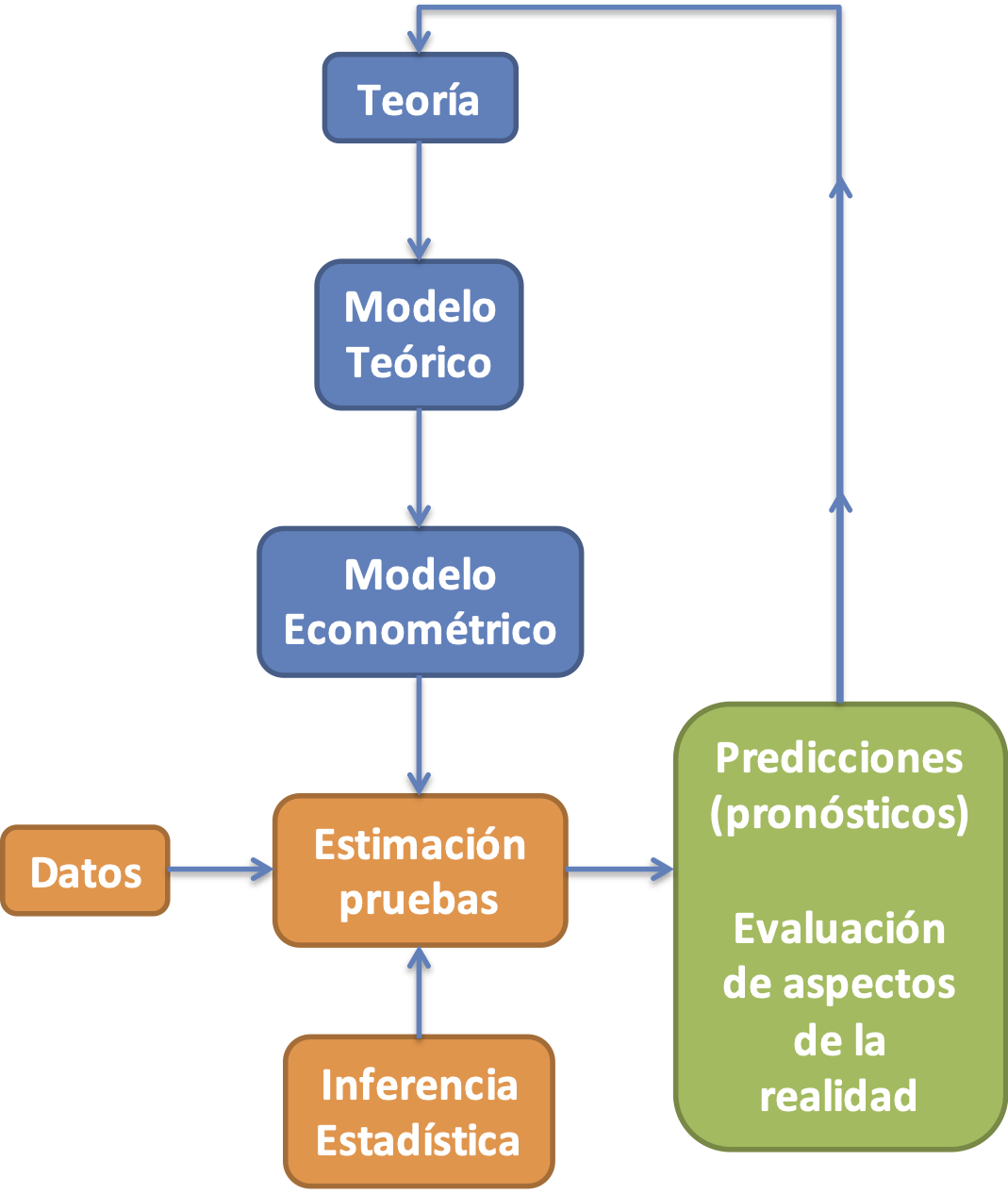
Para lograr su objetivo, la econometría emplea una ruta metodológica que parte de un modelo teórico; es decir, de una formulación matemática de alguna teoría, como se muestra en la Figura 1.9 que fue adaptada de Spanos (1986).
Luego, el econometrista transforma este modelo teórico en un modelo estadístico o econométrico. El modelo econométrico será construido con variables medibles que suponemos representan adecuadamente los conceptos teóricos y se le añade un término de error.
En un siguiente paso, el econometrista estima el modelo usando métodos estadísticos que implican supuestos explícitos e implícitos y datos reales. Si alguno de los supuestos del modelo no se cumple, el econometrista debe corregir el modelo al especificar adecuadamente el término de error o solucionando el problema que está generando la violación del supuesto. Esto se hace para que la herramienta estadística (econométrica) se comporte bien y permita tener confiabilidad en los resultados10.
Una vez el econometrista tiene el modelo estadístico adecuado, procede a comprobar estadísticamente el cumplimiento o no de las restricciones planteadas por la teoría. Si el modelo estimado refleja el comportamiento real adecuadamente, el econometrista pues emplea las estimaciones para hacer predicciones y evaluaciones de los aspectos de la realidad relevantes; en caso contrario, el econometrista deberá empezar el proceso nuevamente, buscando un modelo teórico que explique adecuadamente las relaciones bajo estudio.
Sin embargo, la aproximación del científico de datos es diferente, si bien la herramienta (el modelo clásico de regresión múltiple ) es la misma. En la ciencia de datos no se cuenta con una teoría detrás, pero sí con una cantidad relativamente grande de variables candidatas a ser parte del mecanismo que realmente genera los datos que observamos(el Data Generating Process o DGP)11. Es decir, tenemos datos y no es de interés probar un modelo teórico. En otras palabras, el científico de datos está interesado en encontrar patrones de comportamiento que permitan responder preguntas de negocio y no realizar ciencia en su sentido estricto. Es decir, no es tarea del científico de datos validar modelos teóricos y no tiene como motivación del ejercicio empírico comprobar el cumplimiento o no de una teoría que presente hipótesis. La segunda ruta metodológica que es la que adopta el científico de datos, y menos tradicional en la econometría, implica partir de los datos para encontrar qué variable explican la variable dependiente. En otras palabras, en esta aproximación se interpreta el modelo econométrico como una aproximación al verdadero DGP.
Figura 1.10: Ruta metodológica de los científicos de datos
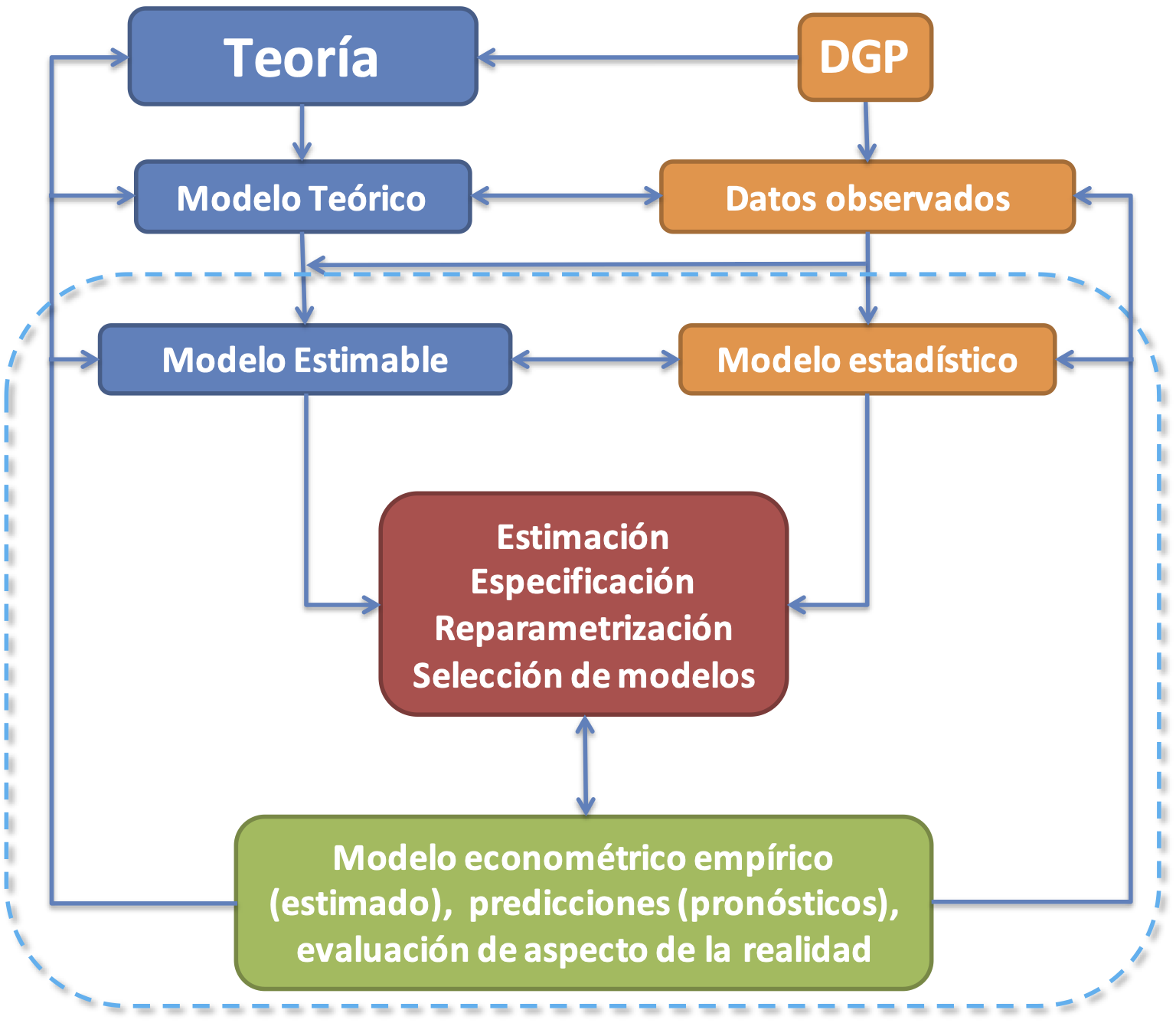
De acuerdo a esta segunda ruta metodológica, que se ilustra en la Figura 1.10, el modelo econométrico usa variables aleatorias disponibles en las bases de datos para especificar una descripción de un mecanismo que genera los datos12.
En la práctica, el científico de datos empleará todas las variables disponibles para explicar la variable de interés y dejará que sean los datos quienes “hablen” para así detectar cuáles variables hacen parte o no del DGP.
No obstante, debido a que es imposible tener variables para todas las características de la realidad13, el modelo estimado por esta ruta metodológica será en todo caso una simplificación de la realidad. A lo largo de este libro, nos concentraremos en el área punteada de la Figura 1.10.
Referencias
Los modelos o algoritmos en algunos casos pueden ser útiles para hacer más de una tarea de analítica, como veremos más adelante. Por eso es importante distinguir entre la tarea de analítica y los modelos y algoritmos.↩︎
En el mundo de la estadística se emplea la expresión “estimar un modelo” para la construcción de un modelo a partir de una muestra. Por otro lado, en el mundo de la inteligencia artificial se emplea la expresión “entrenar un modelo”.↩︎
Los modelos de regresión que se discuten a continuación pueden ser empleados para hacer la tarea de pronosticar.↩︎
Para ver una introducción rápida al tipo de datos que se emplean en el business analytics ver el video disponible en el siguiente enlace: https://youtu.be/2OxY2UTI_Bs.↩︎
Una serie de tiempo es una secuencia de datos que se producen en orden sucesivo a lo largo de un periodo de tiempo. Por ejemplo, el precio del dólar para los últimos 100 días es una serie de tiempo. Otro ejemplo de datos de serie de tiempo son los datos de ventas mensuales, el precio mensual del producto y el gasto en publicidad mensual para los últimos 60 meses.↩︎
En el Capítulo 2 discutiremos ¿qué significa que los resultados sean confiables? y ¿cuáles son los supuestos de esta herramienta?.↩︎
El DGP es la “fórmula” o ley de movimiento que muestra la relación que existe entre las variables explicativas y la variable dependiente. En el siguiente capítulo discutiremos el DGP en detalle.↩︎
Cuando el modelo teórico es el DGP y, por ello, el modelo econométrico difiere del teórico únicamente por razones puramente aleatorias, las dos metodologías coinciden.↩︎
Es decir, todas las variables asociadas al mecanismo que genera los datos.↩︎