8 Multicolinealidad

Objetivos del capítulo

Al finalizar este capítulo, el lector estará en capacidad de:

• Identificar los diferentes síntomas que presenta un modelo estimado en presencia de multicolinealidad.
• Efectuar con R diferentes pruebas formales, con el fin de detectar multicolinealidad en el modelo.
• Decidir si los problemas generados por la multicolinealidad se deben o no solucionar.
• Solucionar, de ser necesario, el problema de multicolinealidad empleando R.

8.1 Introducción

Como lo habíamos discutido en capítulos anteriores, si el modelo de regresión múltiple cumple con los supuestos que se resumen en el recuadro abajo, entonces el Teorema de Gauss-Markov demuestra que los estimadores MCO son MELI (Mejor Estimador Lineal Insesgado) y, por lo tanto, tienen la menor varianza posible cuando se comparan con todos los estimadores lineales posibles.

Supuestos del modelo de regresión múltiple

En resumen, los supuestos del modelo de regresión múltiple son:

1 Relación lineal entre \(y\) y \({X_2},{X_3}, \cdots ,{X_k}\)

2 \({X_2},{X_3}, \cdots ,{X_k}\) son fijas y linealmente independientes (la matriz \(X\) tiene rango completo)

3 El vector de errores \({\bf {\varepsilon}}\) satisface:

• Media cero \(E\left[ {\bf {\varepsilon}} \right] = 0\)
• Varianza constante
• No autocorrelación.

Es decir, \(\varepsilon _i \sim i.i.d\left( {0,\sigma^2} \right)\) o \(\varepsilon _{n \times 1} \sim \left( \bf {0_{n \times 1}},\sigma^2{\bf {I_n}} \right)\).

Ahora veamos qué ocurre si no se cumple una parte del supuesto 2: Las \(X_2 ,X_3 ,\cdots,X_k\) son fijas y linealmente independientes. En especial, que las variables explicativas (Xs) no sean linealmente independientes entre sí. Es importante anotar que la violación de la otra parte del supuesto no tiene grandes implicaciones sobre el resultado que los estimadores MCO sean MELI. En el Anexo al final de este capítulo se presenta la demostración de la insesgadez y eficiencia (Ver sección 8.8) de este estimador si las variables explicativas son estocásticas.

En este capítulo nos concentramos en la violación del supuesto de independencia lineal de las variables explicativas. Este problema que puede presentar un conjunto de datos se conoce con el nombre de multicolinealidad o colinealidad.

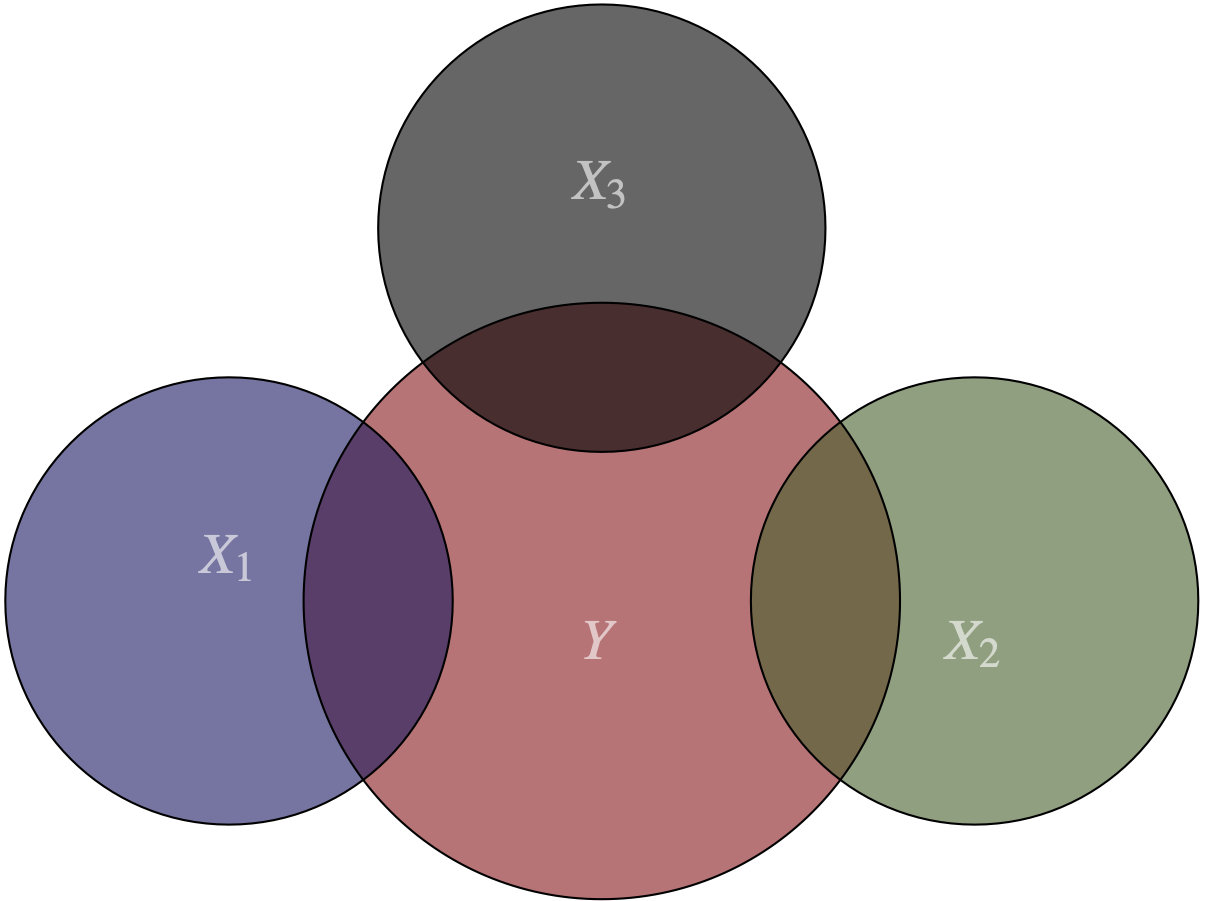
Los supuestos 1 y 2 del teorema de Gauss Markov señalan la existencia de una relación lineal entre las variables explicativas y la dependiente, además de una relación linealmente independiente entre las variables explicativas (X’s). La Figura 8.1 representa estos supuestos. Los círculos representan las variables y sus intersecciones la relación entre ellas. Podemos observar que existe una relación entre la variable explicada y las independientes⁷⁸, pero a su vez existe independencia entre estas últimas⁷⁹.

Figura 8.1: El supuesto de no multicolinealidad

Fuente: elaboración propia.

El problema de multicolinealidad aparece cuando tenemos algún tipo de relación lineal entre las variables independientes o entre un subconjunto de ellas.

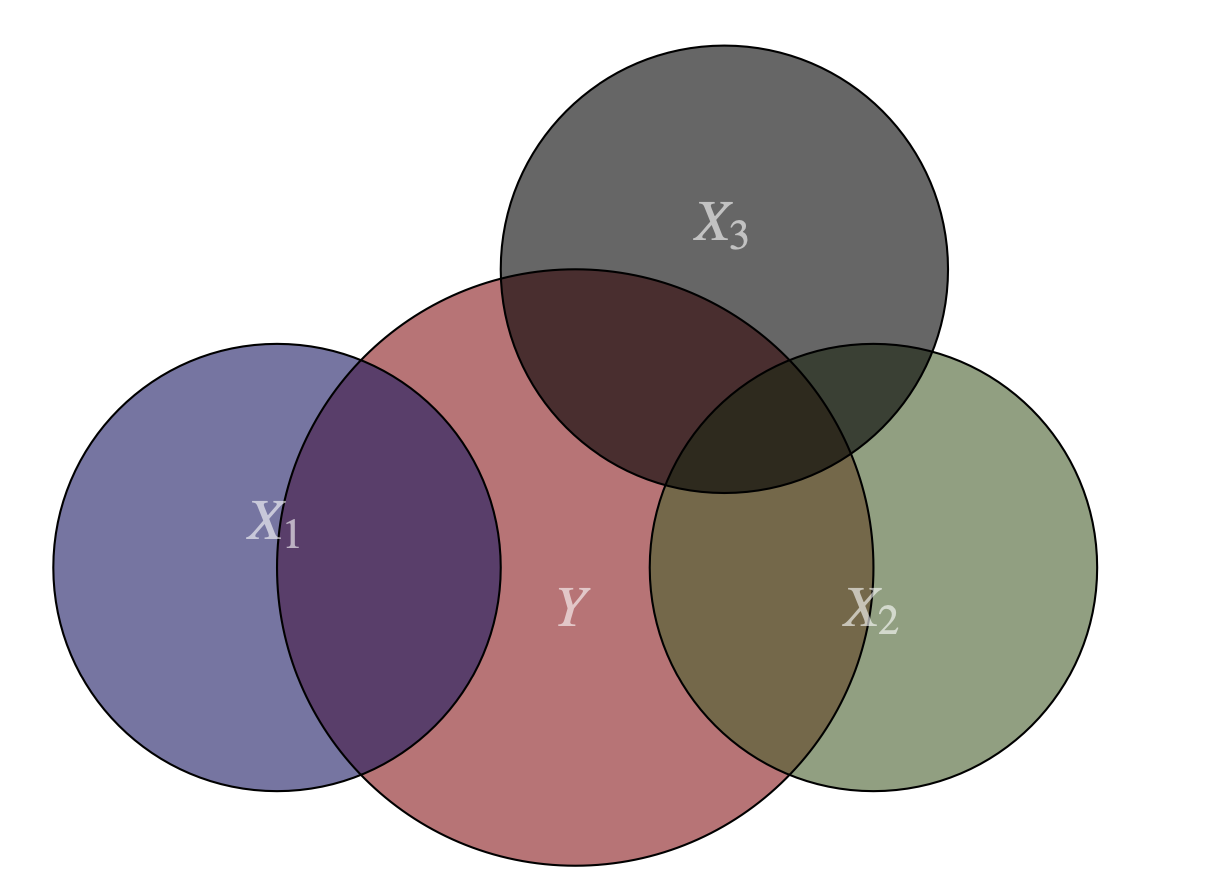
En el siguiente gráfico podemos apreciar la presencia de una relación entre las variables \(X_2\) y \(X_3\); es decir, una parte de la información proporcionada por \(X_2\) está a su vez contenida en la variable \(X_3\). En este caso, si \(X_2\) cambia, esto provoca un cambio directo en \(Y\) (representado por \(\beta_2\)) y también un cambio indirecto; pues al cambiar \(X_2\), \(X_3\) cambia y esto a su vez provoca el cambio en \(Y\). La Figura 8.2 representa esta posibilidad donde el supuesto no se cumple porque existe una relación entre dos variables.

Figura 8.2: Multicolinealidad entre dos variables del modelo

Fuente: elaboración propia.

También podría darse el caso en el que todas las variables independientes o un grupo de ellas se encuentren relacionadas. En la Figura 8.3 se presenta un ejemplo donde todas las variables explicativas comparten la información contenida en cada una de ellas.

Figura 8.3: Multicolinealidad entre tres variables del modelo

Fuente: elaboración propia.

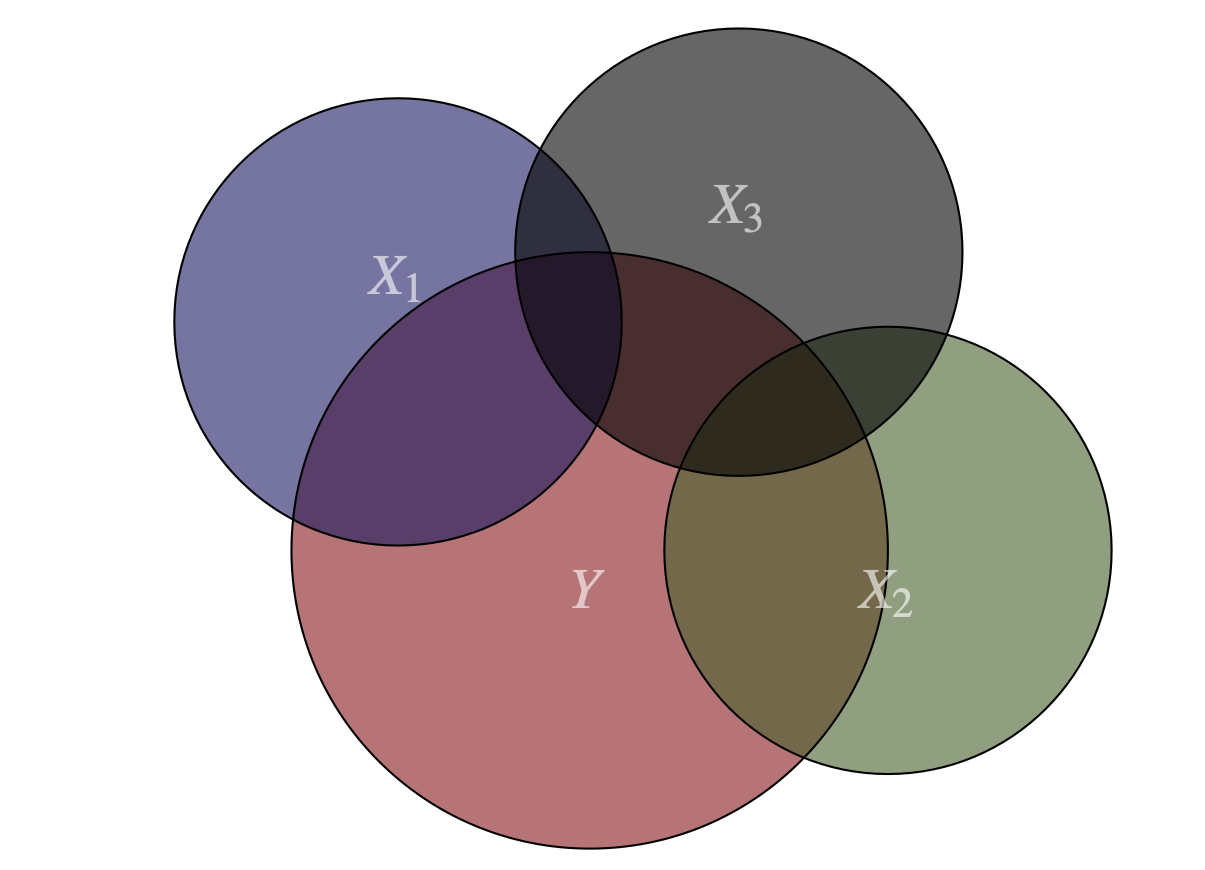
Todos los casos anteriores son ejemplos de multicolinealidad. En la siguiente sección se describen los diferentes grados de este problema. Posteriormente se discute como detectar la existencia de este problema y como solucionar el problema. Finalmente se presenta una aplicación en R.

8.2 Los diferentes grados de multicolinealidad

En general, cuando hay cierto grado de relación lineal entre las variable independientes decimos que existe multicolinealidad (o colinealidad). En la práctica, tendremos diferentes grados de multicolinealidad. Por ejemplo, en la Figura 8.4 se presentan los cuatro posibles grados o tipos de multicolinealidad.

Figura 8.4: Grados de multicolinealidad

Fuente: elaboración propia.

Fuente: elaboración propia.

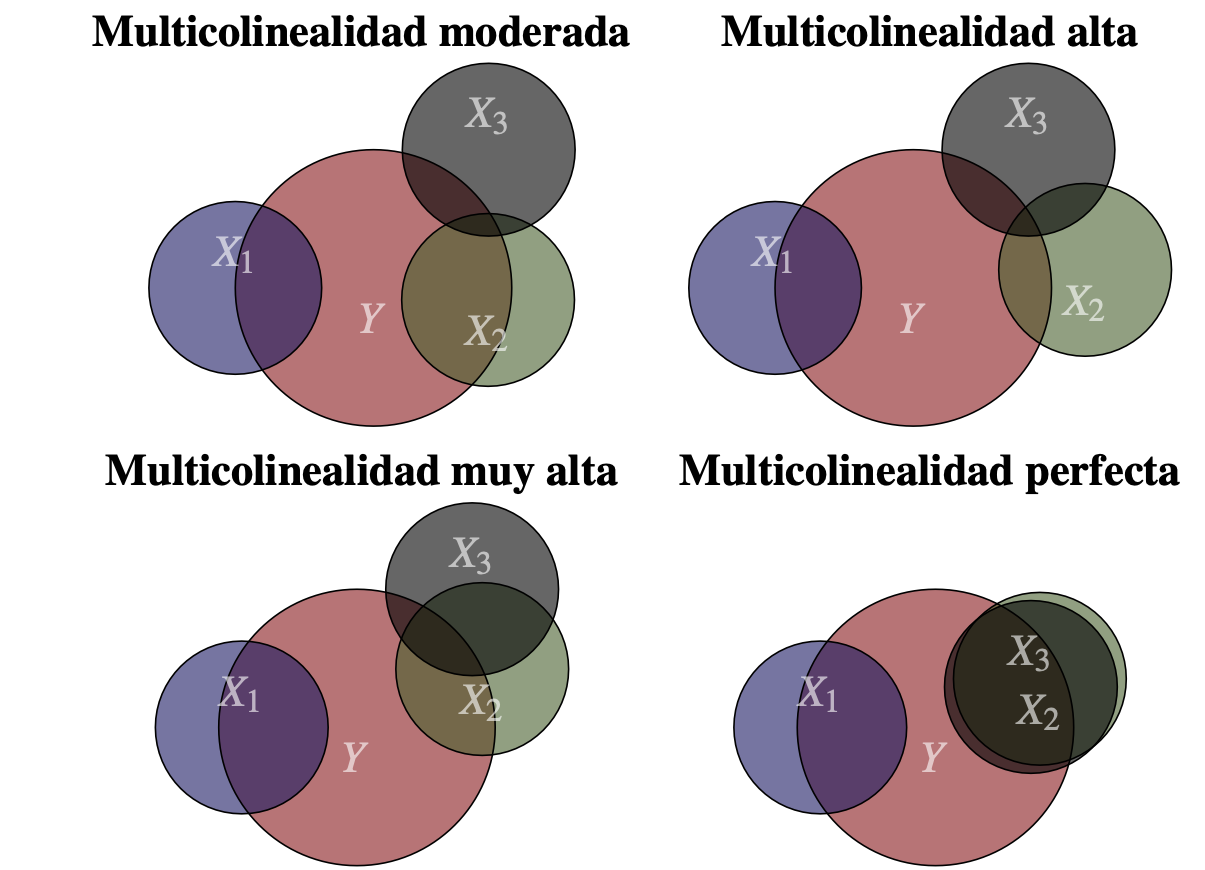
A continuación discutiremos las implicaciones de la multicolinealidad, primero la multicolinealidad perfecta y sus efectos.

8.2.1 Multicolinealidad perfecta

Partamos de un ejemplo, supongamos que queremos explicar la relación entre el peso en kilogramos de un individuo (\(k{g_i}\)) con las horas diarias promedio de actividad física (\(ha_i\),) y las calorías consumidas. Veamos qué sucede si empleamos el siguiente modelo: \[\begin{equation*} k{g_i} = {\beta_0} + {\beta_1}h{a_i} + {\beta_2}c{d_i} + {\beta_3}c{s_i} + {e_i} \end{equation*}\] donde \(cd_i\) y \(cs_i\) corresponden a las calorías consumidas por día y calorías consumidas por semana por el individuo \(i\), respectivamente.

Las variables \(cd_i\) y \(cs_i\) presentan una relación lineal perfecta (multicolinealidad perfecta) debido a que siempre vamos a tener que \(7 \times c{d_i} = c{s_i}\) y, por lo tanto, las X’s no son linealmente independientes entre sí.

Matricialmente este hecho se puede representar de la siguiente manera:

\[\begin{equation} {\bf {y}} = {\left[ {\begin{array}{*{20}{c}} {k{g_1}} \\ {k{g_2}} \\ \vdots \\ {k{g_n}} \\ \end{array}} \right]_{n \times 1}}\quad \quad {\bf {X}} = {\left[ {\begin{array}{*{20}{c}} 1 & {h{a_1}} & {c{d_1}} & {7c{d_1}} \\ 1 & {h{a_2}} & {c{d_2}} & {7c{d_2}} \\ 1 & {h{a_3}} & {c{d_3}} & {7c{d_3}} \\ 1 & {h{a_4}} & {c{d_4}} & {7c{d_4}} \\ 1 & {h{a_5}} & {c{d_5}} & {7c{d_5}} \\ \vdots & \vdots & \vdots & \vdots \\ \end{array}} \right]_{n \times 4}} \tag{8.1} \end{equation}\]

Nota que la cuarta columna de la matriz \(\bf {X}\) es una combinación lineal del vector columna 3 (Ver la sección 14.7 para una discusión del concepto de combinación lineal de vectores). Cuando existe multicolinealidad perfecta, una columna es combinación lineal de otra y otras columnas.

Las consecuencias de esta relación entre dos columnas de la matriz \(\bf X\) es que ésta no tendrá rango columna completo y, por tanto, \({{\bf{X}}^{\bf{T}}}{\bf{X}}\) no tendrá rango completo. Es decir, \(\det ({{\bf{X}}^{\bf{T}}}{\bf{X}}) = 0\). Así, \({\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}\) no existirá y \(\hat \beta = {\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}{{\bf{X}}^{\bf{T}}}{\bf{y}}\) no existirá⁸⁰. En este caso, si queremos eliminar la multicolinealidad perfecta entre \(cd_i\) y \(cs_i\), debemos eliminar cualquiera de las dos variables. No importa cuál se elimine, ya que ambas están aportando la misma información al modelo.

En resumen, el problema que se presenta en presencia de multicolinealidad perfecta es que las columnas de la matriz de las \(X's\) no son linealmente independientes y esto implicará que el estimador de MCO no existirá. Si un modelo presenta multicolinealidad perfecta, entonces la función lm() elimina automáticamente una de las variables involucradas en el problema.

Intuitivamente, el problema de multicolinealidad perfecta implica que la información contenida en una variable es redundante pues esta información ya se recoge en otras variables explicativas. Así el problema de multicolinealidad perfecta es un problema de cómo se plantea el modelo y en consecuencia es fácil de solucionar.

También es posible estar expuesto a la presencia de multicolinealidad perfecta al utilizar variables dummy. Por ejemplo, supongamos que queremos ver el efecto del sector de la economía donde se emplea un individuo sobre el salario (\(w_i\)). Supongamos que el modelo, sin tener en cuenta el efecto del sector económico, es:

\[\begin{equation} w_i = {\lambda _1} + {\lambda _2}\left( {{E_i}} \right) + {\lambda _3}\left( {{C_i}} \right) + {\mu _i} \tag{8.2} \end{equation}\] donde \(E_i\) y \(C_i\) representan los años de educación y los años de capacitación del individuo \(i\) respectivamente.

Ahora, supongamos que la economía tiene tres diferentes sectores: primario (Agricultura, minería, ganadería, etc.), secundario (Manufacturas, etc.), terciario (Comercio, servicios, etc.) y además un individuo solo puede recibir un salario si trabaja en uno de esos tres sectores.

Esto implica generar las siguientes variables dummy:

\[\begin{equation*} D_{1i} = \left\{ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array}} \right.\begin{array}{*{20}c} {\rm {si \: i \in Sec. \: Primario}} \\ {\rm{o.w.}} \\ \end{array} \end{equation*}\]

\[\begin{equation*} D_{2i} = \left\{ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array}} \right.\begin{array}{*{20}c} {\rm {si \: i \in Sec. \: Secundario}} \\ {\rm{o.w.}} \\ \end{array} \end{equation*}\]

\[\begin{equation*} D_{3i} = \left\{ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array}} \right.\begin{array}{*{20}c} {\rm {si \: i \in Sec. \: Terciario}} \\ {\rm{o.w.}} \\ \end{array}, \end{equation*}\]

entonces, nuestro modelo se convierte en⁸¹: \[\begin{equation*} w_i = \lambda _1 + \lambda _2 \left( {E_i } \right) + \lambda _3 \left( {C_i } \right) + \lambda _4 D_{1i} + \lambda _5 D_{2i} + \lambda _6 D_{3i} + \mu _i. \end{equation*}\]

Si analizamos la expresión matricial de este modelo, nos damos cuenta rápidamente del problema que aparece. Matricialmente el modelo será:

\[\begin{equation*} {\bf {y}} = \left[ {\begin{array}{*{20}c} {w_1 } \\ {w_2 } \\ \vdots \\ {w_n } \\ \end{array}} \right]_{n \times 1} {\bf {X}} = \left[ {\begin{array}{*{20}c} 1 & {E_1 } & {C_1 } & 1 & 0 & 0 \\ 1 & {E_2 } & {C_2 } & 0 & 0 & 1 \\ 1 & {E_3 } & {C_3 } & 0 & 1 & 0 \\ 1 & {E_4 } & {C_4 } & 0 & 0 & 1 \\ 1 & {E_5 } & {C_5 } & 0 & 0 & 1 \\ 1 & {E_6 } & {C_6 } & 1 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \end{array}} \right]_{n \times 6} \end{equation*}\]

Para todas las observaciones, tenemos que \(D_{1i} + D_{2i} + D_{3i} = 1\). Además, la columna de la constante será igual a 1 en cada observación. Por lo anterior, concluimos que las \(X's\) no son linealmente independientes, al existir una combinación lineal de las columnas 4, 5 y 6 que es exactamente igual a la primera columna.

Si queremos no tener multicolinealidad perfecta entre las variables dummy y el intercepto debemos eliminar una de las dummy obteniendo el siguiente modelo:

\[\begin{equation*} w_i = \lambda _1 + \lambda _2 \left( {E_i } \right) + \lambda _3 \left( {C_i } \right) + \lambda _4 D_{1i} + \lambda _5 D_{2i} + \mu _i \end{equation*}\] Ahora, \[\begin{equation*} D_{1i} + D_{2i} \ne 1{\rm{ }}\:\:\: \forall i \end{equation*}\] y, por tanto, no hay relación lineal entre las dummy y el intercepto.

En general cuando usamos variables dummy tenemos que tener cuidado si existen \(j\) posibilidades diferentes, entonces usamos \(j-1\) variables dummy, o \(j\) variables dummy y quitamos el intercepto, así evitamos la multicolinealidad perfecta. Esto permite evitar la “trampa de las variables dummy”.

8.2.2 Multicolinealidad no perfecta

En la práctica, el problema de multicolinealidad perfecta es muy raro, pero sí es común contar con modelos con variables independientes altamente correlacionadas entre sí, sin que esta relación sea perfecta. Supongamos que dos o más variables están relacionadas (pero no de manera perfecta), en este caso se tendrá que el \(\det \left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right) = \left| {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right|\) existe, pero tiende a cero. Por lo tanto, la matriz \({\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}\) si existe pero en general tendrá valores muy grandes. Recuerda que: \({\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}} = \frac{1}{{\left| {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right|}}Adj\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)\).

Como la matriz de varianzas y covarianzas de los coeficientes estimados depende de la matriz⁸² \({\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}\), entonces las varianzas de los \(\beta's\) tenderán a ser a su vez muy grandes. Esto implica que los t-calculados de los \(\beta's\) para probar la significancia de los coeficientes estimados sean relativamente bajos⁸³, y así se tenderá a no rechazar la hipótesis nula de no significancia individual de los coeficientes. Así mismo una matriz \({\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}\) con valores relativamente grandes, implicará que la suma cuadrada de la regresión (\(SSR = {\left( {{{\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)}^{ - 1}}{{\bf{X}}^{\bf{T}}}{\bf{y}}} \right)^T}{{\bf{X}}^{\bf{T}}}{\bf{y}} - n{{\bf{\bar y}}^2}\)) será relativamente grande y, por tanto, el \(R^2\) y el \(F-Global\) serán relativamente grandes ya que estos dependen del \(SSR\).

Así, los síntomas más comunes de la multicolinealidad no perfecta⁸⁴ se pueden resumir de la siguiente manera:

1. \(t\) calculados bajos acompañados de \(F-Global\) y \(R^2\) altos

2. Sensibilidad de los \(\beta's\) estimados a cambios pequeños en la muestra⁸⁵

3. Sensibilidad de los \(\beta's\) a la inclusión o exclusión de regresores

No obstante, la multicolinealidad no perfecta provoca estos síntomas, en muchos casos este problema es ignorado por los científicos de datos. Una razón para ignorar la existencia de la multicolinealidad no perfecta es que se privilegie un \(R^2\) alto para el problema bajo estudio. En especial, si la interpretación de los coeficientes no es importante, pero si se desea generar buenas predicciones (se está haciendo analítica predictiva ), entonces se podría privilegiar la existencia de este problema en vez de entrar a solucionarlo. En todo caso, siempre es mejor saber si este problema existe o no, ya sea que se ignore o no.

Por otro lado, existen algunas técnicas estadísticas que permiten lidiar con el problema de la multicolinealidad no perfecta, como por ejemplo la ridge regression o el método de componentes principales para condensar la información de las variables relacionadas en una sola. Pero en la realidad las prácticas más empleadas por los científicos de datos para “lidiar” con la multicolinealidad no perfecta son:

• Descartar una variable de las que presentan el problema.

• Transformar las variables relacionadas, de tal forma que el modelo involucre razones de las variables y no las variables en sus niveles.

• Aumentar la muestra. Al aumentar la muestra, se puede brindar más información que permita mejorar la precisión en la estimación de los coeficientes y, por tanto, la disminución del error estándar de estos. El problema con esta aproximación es que en la mayoría de los casos el científico de datos emplea la mayor cantidad de datos disponibles para el problema y aumentar la muestra es una misión casi imposible.

• No hacer nada. Si bien se identifica la presencia de este problema, en muchos casos no se realiza algún procedimiento para resolverla, pues la multicolinealidad no perfecta no afecta las propiedades MELI de los MCO⁸⁶. El problema aparece en la interpretación de los coeficientes y en algunos casos en la reducción de los t-calculados que podrían ser lo suficientemente grandes como para rechazar la nula de no significancia si la multicolinealidad no perfecta no estuviese presente. Así, si ésta es la opción que se adopta para “lidiar” con la multicolinealidad, entonces se tendrá que ser muy cuidadoso con la interpretación de los coeficientes y con la inferencia respecto a estos.

En conclusión, de encontrarse multicolinealidad no perfecta en un modelo se debe ser muy cauteloso en la interpretación del \(R^2\) y de los coeficientes, así como su significancia. Por otro lado, si el objetivo del modelo estimado con multicolinealidad es la de producir predicciones, entonces el problema de multicolinealidad no es muy importante, siempre y cuando la relación entre las variables explicativas se mantenga para la muestra que se desea predecir.

8.3 Pruebas para la detección de multicolinealidad

Además de chequear los síntomas, en la práctica es necesaria la utilización de pruebas más formales con el fin de detectar la presencia de multicolinealidad no perfecta. A continuación, se describen tres de las pruebas más utilizadas para este fin⁸⁷.

8.3.1 Factor de Inflación de Varianza (VIF)

Dado que uno de los síntomas de la multicolinealidad no perfecta es que los errores estándar de los coeficientes estimados por el método de MCO (y por tanto su varianza) es más grande de lo que debería ser, una forma de detectar la existencia de este problema es mirar cómo se “infla” la varianza de un coeficiente por no ser este independiente a los demás. En otras palabras, el Factor de Inflación de Varianza (\(VIF\) por su sigla en inglés que viene del término Variance Inflation Factor) compara cuál hubiese sido la varianza de un coeficiente determinado si la correspondiente variable fuera totalmente independiente a las demás con el valor realmente observado de dicha varianza. Así, el \(VIF\) mide cuántas veces se aumentó la varianza de un coeficiente por la existencia de un posible problema de multicolinealidad no perfecta.

EL \(VIF\) para el coeficiente \(j\) se define como: \[\begin{equation} VIF_j = \frac{1} {{1 - R_j^2 }} \tag{8.3} \end{equation}\]
donde \({R_j^2}\) es el \(R^2\) de la regresión de \(X_j\) en función de los demás regresores. Así, el \(VIF\) muestra el aumento en \(Var \left[ \hat\beta_j \right]\) que puede atribuirse al hecho que esa variable no es ortogonal a las otras variables del modelo.

Algunos autores como Hair et al. (2014) argumentan que si el \(VIF_j\) excede 3.0, entonces se considera que existe un problema de multicolinealidad. Otros autores como Sheather (2009) afirman que un \(VIF_j\) mayor a 4 es síntoma de un problema grande. No obstante, una regla empírica (rule of thumb) muy común en la práctica es considerar el problema de multicolinealidad alta si el \(VIF_j\) es mayor a 10 (Ver por ejemplo Kutner, M. H.; Nachtsheim, C. J.; Neter (2004)). .

8.3.2 Prueba de Belsley, Kuh y Welsh (1980)

Esta prueba diseñada por Belsley et al. (1980) también es conocida con el nombre de prueba Kappa. Esta prueba se basa en los valores propios⁸⁸ de la matriz \({{\mathbf{X}}^T {\mathbf{X}}}\). Ellos demostraron que empleando el valor propio máximo y mínimo de esta matriz es posible detectar la multicolinealidad. La prueba se construye de la siguiente manera:

\[\begin{equation} \kappa = \sqrt {\frac{{\lambda _1 }} {{\lambda _k }}} \tag{8.4} \end{equation}\]
donde \(\lambda _1\) es el valor propio más grande de \({{\mathbf{X}}^T {\mathbf{X}}}\) y \(\lambda _k\) es el valor propio más pequeño. Los autores demostraron que si \(\kappa > 20\) entonces existe un problema de multicolinealidad.

8.4 Soluciones de la multicolinealidad (¡Si se necesitan!)

8.4.1 Regresión de Ridge

Una forma de solucionar el problema de la multicolinealidad es emplear la regresión de Ridge, pero esta solución trae un costo asociado. Esta aproximación es una variante de los MCO, cuyo objetivo es evitar el problema de multicolinealidad modificando la matriz \({{\mathbf{X}}^T {\mathbf{X}}}\). La modificación se realiza de tal manera que \(\det \left( {{\mathbf{X}}^T {\mathbf{X}}} \right)\) se aleja de cero.

El costo de esta aproximación es que los nuevos parámetros estarán sesgados⁸⁹, pero la varianza es más pequeña; es decir, existe un “trade-off” entre varianza y sesgo. Como dicen los economistas, “no hay un almuerzo gratis” pues este método implica la aparición de un nuevo parámetro \(l\).

Cómo establecer este nuevo parámetro se convierte en la gran pregunta de este método. Antes de continuar es importante anotar que la regresión de Ridge es un recurso de última instancia. Solo se emplea cuando la multicolinealidad es casi perfecta.

El estimador de Ridge está definido como: \[\begin{equation} \mathbf{b}\left( l \right)={{\left( {{\mathbf{X}}^{T}}\mathbf{X}+l\mathbf{I} \right)}^{-1}}{{\mathbf{X}}^{T}}y \tag{8.5} \end{equation}\] Esto implica que: \[\begin{equation} {\mathbf{b}}\left( l \right) = \left( {{\mathbf{I}} + l\left( {{\mathbf{X}}^T {\mathbf{X}}} \right)^{ - 1} } \right)^{ - 1} {\hat \beta} \tag{8.6} \end{equation}\]

donde \(l > 0\) y es no estocástico. \(l\) se conoce como el parámetro de reducción de sesgo, y este parámetro se escoge con algoritmos automáticos como por ejemplo el propuesto por Cule & De Iorio (2012). \(l\) también se puede escoger graficando los coeficientes estimados en función de \(l\) y se selecciona \(l\) más pequeño que produce estimadores estables.

8.4.2 Componentes principales

El análisis de componentes principales (PCA) es un procedimiento matemático que sirve para resumir muchas variables en menos variables y que no requiere supuestos. Se emplea cuando se desea incluir el máximo de información posible contenida en un conjunto de variables en un número inferior de variables, las cuales reciben el nombre de componentes principales. Por esto el PCA es conocido como un método de reducción de variables o de reducción de dimensionalidad. Una de sus limitaciones es que solo aplica a variables cuantitativas.

Figura 8.5: Material multimedia: PCA

Fuente: elaboración propia. https://shorturl.at/oBPU3

Es decir, que lo que se quiere obtener es una matriz \(W\), de \(p\) filas con \(k\) columnas, de tal forma que proyectada sobre la matriz \(X\), con \(n\) filas y \(p\) columnas, permita obtener una matriz \(Y\), con \(n\) filas y \(k\) columnas, que contenga el máximo de información posible y un menor número de variables: \[\begin{equation} \mathbf{Y}=\mathbf{X}\mathbf{W} \tag{8.7} \end{equation}\]

Para un mayor discusión de la técnica de PCA se puede consultar Alonso (2020a). Esta aproximación implica los siguientes pasos:

• Paso 1 Estandarizar las variables cuantitativas y explicativas contenidas en la matriz \(\mathbf{X}\) . Es decir, a cada observación de cada variable restarle su respectiva media, y dividirla por su respectiva desviación estándar.
• Paso 2 Calcular la matriz de varianzas y covarianzas, \(S_{X}=\frac{1}{n-1}\left ( {(X-\bar{x})(X-\bar{x})^{T}} \right )\)
• Paso 3 Calcular los vectores propios y valores propios de la matriz de covarianzas y varianzas. El número de vectores propios y valores propios es igual al número de variables explicativas seleccionadas para el análisis.
• Paso 4 Escoger el número de componentes principales \(k\), en este paso es donde sucede la reducción de dimensionalidad de los datos. Para esto organizamos los vectores propios de mayor a menor en función de su valor propio y seleccionamos aquellos que explican una mayor proporción de la varianza total (dividimos la varianza explicada por cada componente por la suma de la varianza total).
• Paso 5 Construir la matriz de proyección \(W\) a partir de los \(k\) vectores propios seleccionados.
• Paso 6 Transformar el conjunto de datos original \(X\) a través de \(W\) para obtener \(Y\).
• Paso 7 Correr el modelo de regresión inicial empleando el conjunto de datos transformado.

8.4.3 Remover variables con alto VIF

Es común que los científicos de datos empleen una aproximación diferente a las dos anteriores para solucionar el problema de la multicolinealidad. Dado que los científicos de datos típicamente se enfrentan a tener una clara variable dependiente y un grupo grande de variables explicativas, una aproximación natural es descartar de manera recursiva las variables del modelo que tengan un \(VIF\) más grande de un determinado umbral (típicamente mayor a 4).

Así, esta aproximación implica los siguientes pasos:

• Paso1 Calcular el \(VIF\) para cada variable explicativa del modelo
• Paso2 Identificar la variable explicativa con el mayor \(VIF\)
• Paso3 Si el mayor \(VIF\) es inferior al umbral determinado (normalmente 4), parar. En caso contrario, re-estimar el modelo sin dicha variable
• Paso4 Regresar al primer paso

De esta manera, se arriba a un modelo con todas las variables con un \(VIF\) relativamente pequeño. Esta solución es muy fácil de automatizar como lo discutiremos en la siguiente sección.

8.5 Práctica en R

El objetivo de este ejercicio es aplicar las tres pruebas de multicolinealidad anteriormente descritas y de ser necesario solucionar dicho problema. En este caso el gerente del hospital de nivel tres “SALUD PARA LOS COLOMBIANOS”, ubicada en la ciudad de Bogotá, se encuentra al frente de una reestructuración de los salarios que recibe su equipo de trabajo con el objetivo de lograr equidad laboral con enfoque de género. Se presume que existen brechas salariales entre hombres y mujeres⁹⁰. Los datos se encuentran disponibles en el archivo DatosMultiColinealidad.csv⁹¹.

La pregunta de negocio es si existe o no una brecha salarial entre hombres y mujeres. Uno de los métodos más utilizados para determinar el efecto de la discriminación en la brecha salarial es la propuesta por Oaxaca (1973), quienes sugieren una técnica para medir la diferencia que tiene sobre el ingreso, características como el capital humano entre géneros. El modelo a estimar es el siguiente: \[\begin{equation} \ln (ih_i) = {\beta_0} + {\beta_1}yedu_i + {\beta_2}exp _i + {\beta_3}exp _i^2 + {\beta_4}{D_i} + {\beta_5}Dexp _i + {\beta_6}Dexp _i^2 + \varepsilon_i \tag{8.8} \end{equation}\] donde, \[\begin{equation*} {\rm{ }}{D_i} = \left\{ {\begin{array}{*{20}{c}} 1 & {\rm{si\: el\: individuo \:} {\textit{$i$}} \rm{\: es \: mujer}} \\ 0 & {o.w.} \\ \end{array}} \right. \end{equation*}\] Además, \(\ln(ih_i)\) representa el logaritmo natural del ingreso por hora del individuo \(i\), \(yedu_i\) y \(exp_i\) denotan los años de educación y de experiencia del individuo \(i\). Antes de analizar los datos, es claro que la especificación de este modelo incluye dos variables que están relacionadas, pero no de manera lineal; es decir, \(exp\) y \(exp^2\). Como la relación es cuadrática y no lineal, no hay razón por la cual esperar, a priori, la presencia de multicolinealidad perfecta o no perfecta.

Como siempre, el primer paso será cargar los datos y constatar que estos quedan bien cargados.

Noten que la variable \(exp _i^2\) no está en el data.frame leído y no es necesaria crearla para estimar el modelo. Empleemos la función lm() del paquete básico de R para estimar el modelo descrito en (8.8).

La notación \(I()\) en la fórmula implica que R hará la operación presentada dentro del paréntesis y se agregará como una variable explicativa. Los resultados de la estimación del modelo se reportan en el Cuadro 8.1. Antes de entrar a calcular los estadísticos para determinar la presencia de multicolinealidad, es importante anotar que los síntomas no están presentes, pero esto no implica la ausencia de multicolinealidad. Recuerden que antes de analizar cualquier resultado es importante estar seguros que no existen problemas de multicolinealidad.

Cuadro 8.1: Modelo de brecha salarial estimado por MCO

(Intercept)	5.86***
	(0.08)
yedu	0.13***
	(0.00)
exp	0.03***
	(0.01)
exp^2	-0.00**
	(0.00)
sexomujer	-0.12
	(0.08)
exp:sexomujer	-0.00
	(0.01)
exp^2:sexomujer	0.00
	(0.00)
R2	0.45
Adj. R2	0.45
Num. obs.	1415
***p < 0.001; **p < 0.01; *p < 0.05

8.5.1 Pruebas de multicolinealidad

8.5.1.1 VIF

Para calcular el \(VIF\) emplearemos el paquete car (Fox & Weisberg, 2019) . Este paquete tiene la función vif() cuyo único argumento es un objeto de clase lm con el modelo estimado.

library(car)
vif(res1)

##          yedu           exp      I(exp^2)          sexo      exp:sexo 
##      1.249719     19.643504     18.080978      7.589628     43.865651 
## I(exp^2):sexo 
##     25.438134

En este caso el \(VIF\) para las variables \(exp\), \(exp^2\), \(sexo\) y la interacción de esta última con las dos anteriores son muy grandes. Por ejemplo, \(exp\) tiene una varianza aproximadamente 20 veces más grande que si las variables no presentan colinealidad.

Claramente, los resultados implican la existencia de un problema delicado de multicolinealidad, no obstante los síntomas no estaban claramente presentes.

8.5.1.2 Prueba de Belsley, Kuh y Welsh (1980)

Para realizar esta prueba es necesario encontrar la matriz \({{\mathbf{X}}^T {\mathbf{X}}}\) y calcular sus valores propios. Esto se puede hacer empleando la función model.matrix() del paquete básico de R que permite obtener la matriz \(\mathbf{X}\). Esta función solo tiene como argumento un objeto de clase lm con el modelo estimado. Los valores propios de una matriz se pueden encontrar empleando la función eigen() .

# matriz X
XTX <- model.matrix(res1)
# se calculan los valores propios
e <- eigen(t(XTX) %*% XTX)
# se muestran los valores propios
e$val

## [1] 1.214720e+09 1.856133e+08 2.232308e+05 2.870475e+04 1.723882e+04
## [6] 1.191735e+02 3.274535e+01

# se crea el valor propio mas grande
lambda.1 <- max(e$val)
# se crea el valor propio mas pequeño
lambda.k <- min(e$val)
# se calcula kappa
kappa <- sqrt(lambda.1/lambda.k)
kappa

## [1] 6090.644

Este estadístico es muy grande (\(\kappa\) = 6090.644165). Esta prueba también coincide en la existencia de un problema serio de multicolinealidad.

Finalmente y teniendo en cuenta los resultados de todas las pruebas efectuadas, podemos concluir que el modelo presenta un alto grado de multicolinealidad. Esto probablemente se debe a la alta correlación entre las variables \(exp\) y \(exp^2\). De la definición de las variables sabemos que no existe una relación lineal perfecta, pero nuestro hallazgo puede ser síntoma de que los valores de la variable \(exp\) corresponden a un rango relativamente corto, para el cual la relación exponencial puede ser aproximada por una relación lineal. Ahora bien, no estamos frente a un problema de multicolinealidad perfecta, y por lo tanto no se está violando el segundo supuesto del teorema de Gauss Markov. Por otro lado, el modelo teórico que se emplea para calcular las brechas salariales necesita incluir en la especificación ambas variables por razones bien fundamentadas en Oaxaca (1973) y sería incorrecto eliminar alguna de las dos variables.

Ahora tu puedes proceder a determinar si existe o no diferencias salariales entre las mujeres y los hombres para esta muestra.

8.5.2 Solución del problema removiendo variables con alto VIF

Ahora supongamos que si se deseara solucionar el problema de multicolinealidad. Nota que en este caso en específico esto no parece una buena opción, pero de todas maneras procederemos a resolver el problema solo para ejemplificar la técnica.

Creemos una función que permite eliminar de manera automática e iterativa las variables cuyos respectivos coeficientes tengan un \(VIF\) superior a un umbral determinado (\(u\)). La función remueve.VIF.grande() se presenta a continuación, sigue con detalle cada línea de la función para entender los “trucos” que se emplean.

remueve.VIF.grande <- function(modelo, u){ 
  require(car)
  # extrae el dataframe 
  data <-  modelo$model
  # Calcula todos los VIF 
  all_vifs <- car::vif(modelo)
  # extraer el nombre de todas las variables X 
  names_all <- names(all_vifs)
  # extraer el nombre de la variables y 
  dep_var <- all.vars(formula(modelo))[1]

  # Remover las variables con  VIF > u 
  # y reestimar el modelo con las otras variables

  while(any(all_vifs > u)){
    # elimina variable con max vif
    var_max_vif <- names(which(all_vifs == max(all_vifs))) 
    # remueve la variable
    names_all <- names_all[!(names_all) %in% var_max_vif]  
    # nueva fórmula
    myForm <- as.formula(paste(paste(dep_var, "~ "),
                paste (names_all, collapse=" + "), sep=""))
    # creando el nuevo modelo con nueva fórmula
    modelo.prueba <- lm(myForm, data= data)  
    all_vifs <- car::vif(modelo.prueba)
  }
  modelo.limpio <- modelo.prueba
  return(modelo.limpio)
}

La función que acabamos de construir (remueve.VIF.grande()) tiene dos argumentos, el primero es un objeto de clase lm y el segundo el umbral para el \(VIF\).

No obstante, no es necesario solucionar el problema de multicolinealidad en el caso del modelo estudiado. A continuación, se muestra un ejemplo de cómo emplear la función remueve.VIF.grande().

res2 <- remueve.VIF.grande(res1, 15)
summary(res2)  

## 
## Call:
## lm(formula = myForm, data = data)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -3.11988 -0.29420 -0.00166  0.30334  2.63580 
## 
## Coefficients:
##                      Estimate Std. Error t value Pr(>|t|)    
## (Intercept)         5.874e+00  6.593e-02  89.090  < 2e-16 ***
## yedu                1.307e-01  3.979e-03  32.846  < 2e-16 ***
## exp                 3.204e-02  3.918e-03   8.178 6.39e-16 ***
## I(exp^2)           -2.616e-04  7.688e-05  -3.402 0.000687 ***
## sexomujer          -1.539e-01  3.977e-02  -3.871 0.000114 ***
## I(exp^2):sexomujer -2.025e-05  4.902e-05  -0.413 0.679642    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5742 on 1409 degrees of freedom
## Multiple R-squared:  0.4542, Adjusted R-squared:  0.4522 
## F-statistic: 234.5 on 5 and 1409 DF,  p-value: < 2.2e-16

vif(res2)

##          yedu           exp      I(exp^2)          sexo I(exp^2):sexo 
##      1.248258     10.134731     10.214214      1.696079      2.584824

8.5.3 Solución del problema empleando la regresión de Ridge

Como se mencionó anteriormente, no estamos frente a un problema de multicolinealidad perfecta o casi perfecta, y no se está violando el segundo supuesto del teorema de Gauss Markov, por lo que no deberíamos emplear la regresión de Ridge, ya que ésta sólo se utiliza como un recurso de última instancia. Sin embargo, si quisiéramos emplearla podríamos utilizar la función linearRidge() del paquete (Cule et al., 2021). Los argumentos más importantes de esta función son: linearRidge(formula, data, lambda, scaling)

donde:

• formula: fórmula del modelo de regresión.
• data: objeto de clase data.frame que contiene los datos
• lambda forma en la que se va a hallar el \(l\). El valor por defecto es automático, es decir se encuentra de manera automática el parámetro de reducción de sesgo \(l\), si esto no se desea se puede colocar un vector con los valores de \(l\) que se desean probar.
• scaling: el valor por defecto es corrform que ajusta los valores de las variables explicativas de tal forma que la matriz de correlaciones sea unitaria en la diagonal.

Un ejemplo de cómo emplear esta función se presenta a continuación.

## 
## Call:
## linearRidge(formula = Lnih ~ yedu + exp + I(exp^2) + sexo + sexo * 
##     exp + sexo * I(exp^2), data = datos)
## 
## 
## Coefficients:
##                      Estimate Scaled estimate Std. Error (scaled)
## (Intercept)         6.233e+00              NA                  NA
## yedu                1.131e-01       1.823e+01           5.604e-01
## exp                 1.431e-02       6.676e+00           6.188e-01
## I(exp^2)            1.340e-05       3.198e-01           6.242e-01
## sexomujer          -1.539e-01      -2.893e+00           6.105e-01
## exp:sexomujer       1.403e-03       6.810e-01           5.195e-01
## I(exp^2):sexomujer -4.618e-05      -8.699e-01           6.117e-01
##                    t value (scaled) Pr(>|t|)    
## (Intercept)                      NA       NA    
## yedu                         32.525  < 2e-16 ***
## exp                          10.788  < 2e-16 ***
## I(exp^2)                      0.512    0.608    
## sexomujer                     4.739 2.15e-06 ***
## exp:sexomujer                 1.311    0.190    
## I(exp^2):sexomujer            1.422    0.155    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Ridge parameter: 0.118604, chosen automatically, computed using 2 PCs
## 
## Degrees of freedom: model 3.89 , variance 3.152 , residual 4.627

## 
##  lambda 0.118604 chosen automatically using 2 PCs
## 
##                    Estimate (scaled) Std. Error (scaled) t value (scaled)
## yedu                         18.2284              0.5604           32.525
## exp                           6.6762              0.6188           10.788
## I(exp^2)                      0.3198              0.6242            0.512
## sexomujer                    -2.8932              0.6105            4.739
## exp:sexomujer                 0.6810              0.5195            1.311
## I(exp^2):sexomujer           -0.8699              0.6117            1.422
##                    Pr(>|t|)    
## yedu                < 2e-16 ***
## exp                 < 2e-16 ***
## I(exp^2)              0.608    
## sexomujer          2.15e-06 ***
## exp:sexomujer         0.190    
## I(exp^2):sexomujer    0.155    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

8.5.4 Solución del problema empleando componentes principales

Si quisiéramos emplear PCA para solucionar un problema de multicolinealidad podríamos emplear la función lm(princomp) del paquete base de R. Ésta permite calcular los PCA empleando la matriz de varianzas y covarianzas o empleando la matriz de correlaciones. Vamos a emplear la matriz de correlaciones para el cálculo. Para un mayor discusión de la técnica de PCA se puede consultar Alonso (2020a).

Los argumentos más importantes de esta función son: princomp(formula, data, cor=TRUE)

donde: + formula: fórmula con las variables independientes numéricas, no incluir la variable dependiente

• data: objeto de clase data.frame que contiene los datos

• cor: indica si se va a calcular los PC empleando la matriz de varianzas y covarianzas o empleando la matriz de correlaciones

Los componentes principales se calculan de manera sencilla con el siguiente código:

res.pca <- princomp(~yedu + exp + I(exp^2), data=datos)

summary(res.pca)

## Importance of components:
##                             Comp.1       Comp.2       Comp.3
## Standard deviation     634.6930542 4.026690e+00 3.775598e+00
## Proportion of Variance   0.9999244 4.024724e-05 3.538434e-05
## Cumulative Proportion    0.9999244 9.999646e-01 1.000000e+00

Ahora decidamos el número de componentes. Para esto podemos emplear un gráfico de codo (*elbow graph** también conocido como scree plot). Para esto es necesario mirar la proporción de la varianza de todos los datos explicada por cada componente principal.

El primer paso, es calcular la desviación estándar de cada componente y la varianza.

std_dev <- res.pca$sdev
pr_var <- std_dev^2
pr_var

##       Comp.1       Comp.2       Comp.3 
## 402835.27299     16.21424     14.25514

Nuestro objetivo es encontrar los componentes que explican la mayor varianza. Recuerden que queremos conservar tanta información como sea posible utilizando estos componentes. Entonces, cuanto mayor sea la varianza explicada, mayor será la información contenida en esos componentes.

Para calcular la proporción de la varianza explicada por cada componente, simplemente dividimos la varianza por la suma de la varianza total. Esto resulta en:

prop_varex <- pr_var/sum(pr_var)
prop_varex

##       Comp.1       Comp.2       Comp.3 
## 9.999244e-01 4.024724e-05 3.538434e-05

Noten que el primer componente principal explica el 99.9% de la varianza. Aunque parece evidente que debemos quedarnos con el primer componente, ¿cómo decidimos cuántos componentes deberíamos seleccionar para la etapa de modelado cuando no es tan clara la respuesta?

La respuesta a esta pregunta es proporcionada por un elbow graph y un gráfico acumulado de varianza (Ver figura 8.6.

par(mfrow=c(1,2))
 plot(prop_varex, xlab = "Componente principal",
      
      ylab = "Proporción explicada de la varianza (PVE)",
      
      type = "b")

plot(cumsum(prop_varex), xlab = "Componente principal",
     
     ylab = "Proporción explicada de la varianza acumulada",
     
     type = "b")

Figura 8.6: Proporción de la varianza explicada por cada PCA y acumulada

Fuente: elaboración propia.

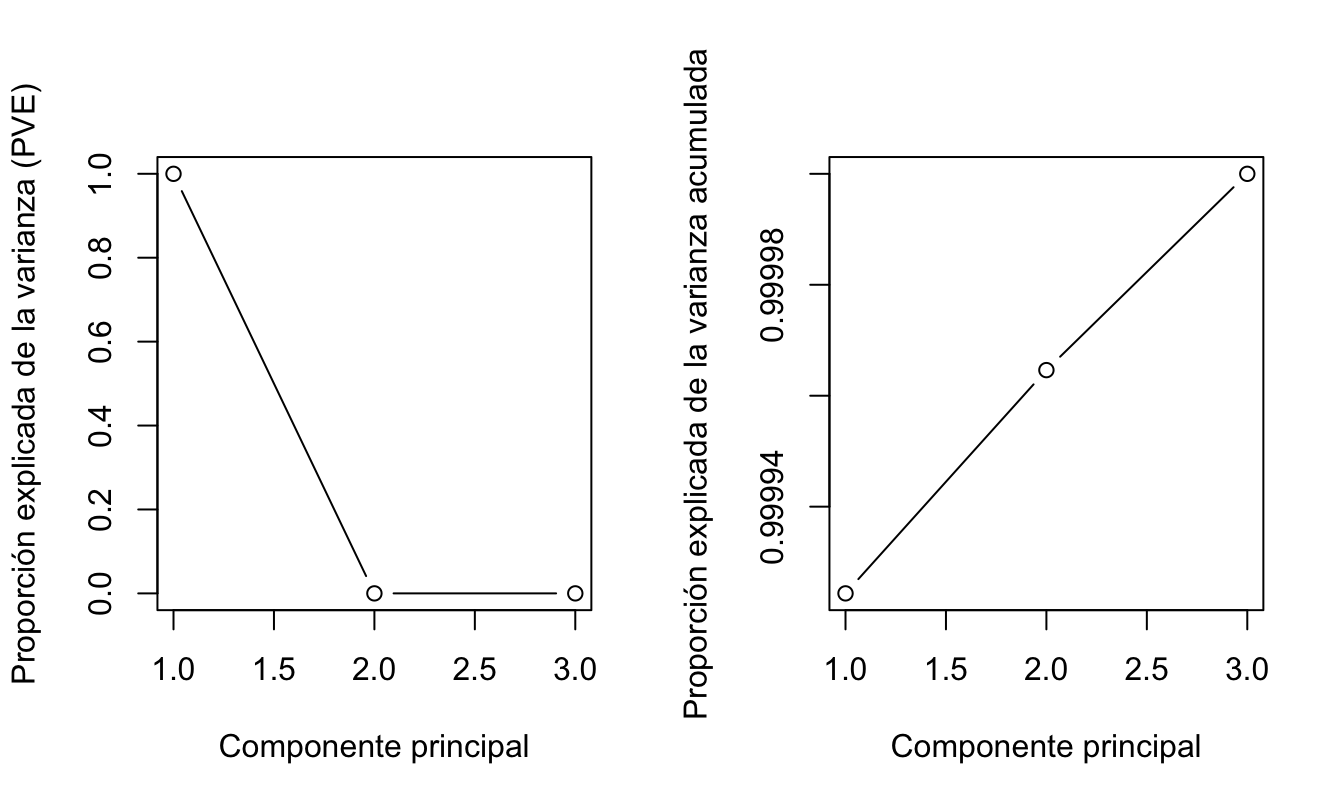
En este tipo de gráficos se busca el “codo” (elbow). En este caso no se observa el codo, es decir la información se resume en el primer componente. Finalmente se extraen la matriz proyectada (valores de los componentes principales que remplazarán a las variables originales), los cuales vamos a emplear en estimar de nuevo el modelo inicial.

head(res.pca$scores)
PCA.res <- res.pca$scores[,1]
head(PCA.res)

res2 <- lm(Lnih ~  sexo + PCA.res, datos)
summary(res2)

Noten que en este caso es imposible interpretar el coeficiente asociado al componente principal.

Ahora, podemos reproducir el ejercicio con la descomposición a partir de la matriz de varianzas y covarianza.

res.pca2 <- princomp(~yedu + exp + I(exp^2), data=datos, cor=FALSE)
std_dev2 <- res.pca2$sdev
pr_var2 <- std_dev2^2
pr_var2
prop_varex2 <- pr_var2/sum(pr_var2)
prop_varex2

Y para variar realicemos los gráficos de codo con el paquete ggplot2 (Wickham, 2016) y el paquete gridExtra (Auguie, 2017) (Ver Figura 8.7.

library(gridExtra)
PVEplot <- qplot(c(1:3), prop_varex2) + 
  geom_line() + 
  xlab("Componente Principal") + 
  ylab("PVE") +
  ggtitle("Gráfico de codo") +
  ylim(0, 1)


cumPVE <- qplot(c(1:3), cumsum(prop_varex2)) + 
          geom_line() + 
          xlab("Componente Principal") + 
          ylab(NULL) + 
          ggtitle("Gráfico de codo acumulado") +
          ylim(0,1)

grid.arrange(PVEplot, cumPVE, ncol = 2)

## TableGrob (1 x 2) "arrange": 2 grobs
##   z     cells    name           grob
## 1 1 (1-1,1-1) arrange gtable[layout]
## 2 2 (1-1,2-2) arrange gtable[layout]

Figura 8.7: Gráfico de codo y codo acumulado

Fuente: elaboración propia.

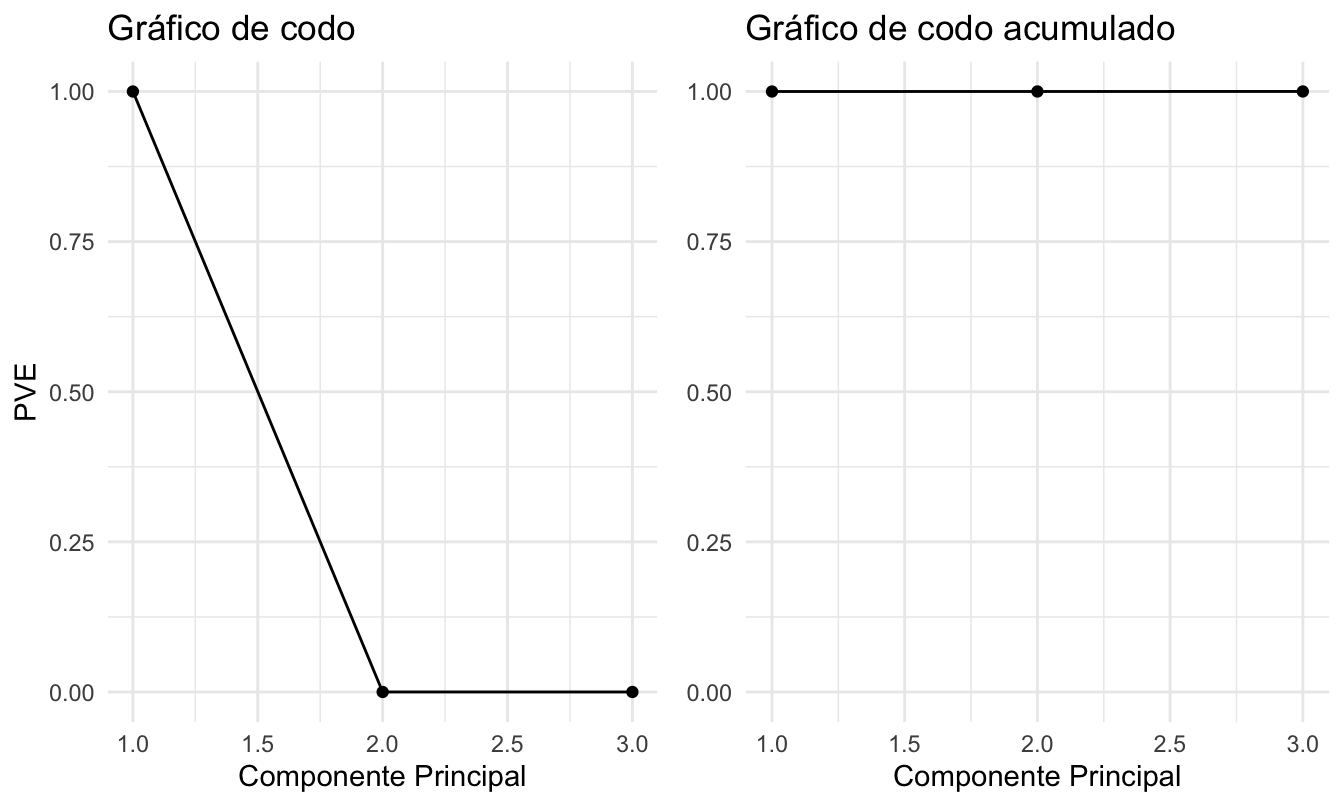
Noten que el resultado es muy similar. Deberíamos emplear 1 componente. Los demás pasos del procedimiento los puede realizar por su cuenta.

8.6 Comentarios finales

En este Capítulo discutimos el problema de multicolinealidad. El problema de multicolinealidad perfecta no permite estimar el modelo, pero es muy fácil de solucionar. Por otro lado, vimos que el problema de multicolinealidad no perfecta es un problema que se manifiesta en \(t\) calculados bajos acompañados de \(F-Global\) y \(R^2\) altos, sensibilidad de los \(\beta's\) estimados a cambios pequeños en la muestra y sensibilidad de los \(\beta's\) a la inclusión o exclusión de regresores.

No obstante, la multicolinealidad no perfecta provoca estos síntomas, en muchos casos este problema es ignorado por los científicos de datos. Una razón para ignorar la existencia de la multicolinealidad no perfecta es que se privilegie un \(R^2\) alto para el problema bajo estudio. En especial, si la interpretación de los coeficientes no es importante, pero si se desea generar buenas predicciones (se está haciendo analítica predictiva), entonces se podría privilegiar la existencia de este problema en vez de entrar a solucionarlo. En todo caso, siempre es mejor saber si este problema existe o no, ya sea que se ignore o no.

8.7 Ejercicios

Las respuestas a estos ejercicios se encuentran en la sección 16.4.

8.7.1 Ejercicio práctico: Fabricante de automóviles

Un científico de datos es contratado por un fabricante de automóviles para estimar un modelo sencillo que le permita predecir cuál debe ser la posición del asiento para un conductor determinado, en otras palabras ¿cuál es la distancia horizontal del punto medio de las caderas desde una ubicación fija en el automóvil?. El fabricante desea que sus carros sean cómodos y seguros. Para elaborar la tarea se cuenta con 38 observaciones (la información se encuentra en el archivo datosmulti.csv⁹²). Las observaciones corresponden a características del conductor como peso, edad, su altura si emplea zapatos o no, su altura sentado, la longitud de muslo, pierna y brazo. Para explicar cuál debe ser la distancia horizontal (\(D_i\) en la base de datos Distancia_centro) no emplearemos por ahora todas las variables disponibles. Estimemos el siguiente modelo:

\[\begin{equation} {D_i} = {\alpha _0} + {\alpha _1}{edad_{i}} + {\alpha _2}{peso_{i}} + {\alpha _3}{alturadescalzo_{i}} + {\alpha _4}{alturadesdezapatos_{i}} + {\varepsilon _t} \tag{8.9} \end{equation}\]

Estime el modelo y determine si existe o no multicolinealidad por medio de las pruebas estudiadas en este capítulo. Adicionalmente, corrija (de ser posible) el problema de multicolinealidad si es que existe. Explique.

8.8 Anexos

8.8.1 Demostración de la insesgadez del estimador MCO con variables explicativas aleatorias

Recordemos que el estimador MCO (\(\hat \beta\)) esta dado por: \[\begin{equation*} \hat \beta = \left( {{\mathbf{X}}^T {\mathbf{X}}} \right)^{ - 1} {\mathbf{X}}^T y \end{equation*}\]
Este estimador se puede reescribir de la siguiente manera:

\[\begin{equation*} \hat \beta = \left( {{\mathbf{X}}^T {\mathbf{X}}} \right)^{ - 1} {\mathbf{X}}^T \left( {{\mathbf{X}}\beta + \varepsilon } \right) \end{equation*}\] \[\begin{equation*} \hat \beta = \left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T {\bf{X}}\beta + \left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T \varepsilon \end{equation*}\] \[\begin{equation*} \hat \beta = \left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T {\bf{X}}\beta + \left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T \varepsilon \end{equation*}\] \[\begin{equation} \hat \beta = \beta + \left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T \varepsilon \tag{8.10} \end{equation}\] Ahora consideremos el valor esperado para un valor dado de \({\bf{X}}\) no aleatorio.
\[\begin{equation*} E\left[ {\hat \beta\left| {\bf{X}} \right.} \right] = E\left[ {\beta + \left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T \varepsilon \left| {\bf{X}} \right.} \right] \end{equation*}\] \[\begin{equation*} E\left[ {\hat \beta\left| {\bf{X}} \right.} \right] = \beta + \left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T E\left[ {\varepsilon \left| {\bf{X}} \right.} \right] \end{equation*}\] Empleando el supuesto de que los errores tienen media cero ( \(E\left[ {\varepsilon \left| {\mathbf{X}} \right.} \right] = 0\) ) se obtiene que: \[\begin{equation*} E\left[ {\hat \beta\left| {\bf{X}} \right.} \right] = \beta \end{equation*}\]

Por otro lado, recordemos la (Ley de valor esperado iterado) que implica: \[\begin{equation*} E\left[ W \right] = E_Z \left[ {E\left[ {W\left| Z \right.} \right]} \right] \end{equation*}\] donde \(E_Z \left[ \cdot \right]\) es el valor esperado considerando todos los posibles valores de \(Z\) y
\(E\left[ {W\left| Z \right.} \right]\) es una función de los valores de \(Z\). Entonces, si \({\bf{X}}\) es aleatorio: \[\begin{equation*} E\left[ \hat \beta \right] = E_{\bf{X}} \left[ {E\left[ {\hat \beta\left| {\bf{X}} \right.} \right]} \right] = E_{\bf{X}} \left[ \beta \right] = \beta \end{equation*}\] Es decir, el estimador MCO \(\hat \beta\) es insesgado aún si las variables explicativas son aleatorias.

8.8.2 Demostración de la eficiencia del estimador MCO con variables explicativas aleatorias

Recordemos que el estimador MCO (\(\hat \beta\)) es un estimador lineal dado por: \[\begin{equation*} \hat \beta = \beta + \left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T \varepsilon \end{equation*}\] Ahora por simplicidad reescribamos el estimador de la siguiente manera: \[\begin{equation*} \hat \beta = \beta + {\bf{A}}\varepsilon \end{equation*}\] donde \({\bf{A}} = \left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T\).

Ahora calculemos la matriz de varianzas y covarianzas del estimador MCO.

\[\begin{equation*} Var\left[ {\hat \beta\left| {\bf{X}} \right.} \right] = E\left[ {\left( {\hat \beta - E\left[ \hat \beta \right]} \right)\left( {\hat \beta - E\left[ \hat \beta \right]} \right)^T \left| {\bf{X}} \right.} \right] \end{equation*}\]
\[\begin{equation*} Var\left[ {\hat \beta\left| {\bf{X}} \right.} \right] = E\left[ {\left( {\hat \beta - \beta } \right)\left( {\hat \beta - \beta } \right)^T \left| {\bf{X}} \right.} \right] \end{equation*}\] \[\begin{equation*} Var\left[ {\hat \beta\left| {\bf{X}} \right.} \right] = E\left[ {\left( {\beta + \left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T \varepsilon - \beta } \right)\left( {\hat \beta - \beta } \right)^T \left| {\bf{X}} \right.} \right] \end{equation*}\] \[\begin{equation*} Var\left[ {\hat \beta\left| {\bf{X}} \right.} \right] = E\left[ {\left( {\left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T \varepsilon } \right)\left( {\left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T \varepsilon } \right)^T \left| {\bf{X}} \right.} \right] \end{equation*}\] \[\begin{equation*} Var\left[ {\hat \beta\left| {\bf{X}} \right.} \right] = E\left[ {\left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T \varepsilon \varepsilon ^T {\bf{X}}\left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} \left| {\bf{X}} \right.} \right] \end{equation*}\]

\[\begin{equation*} Var\left[ {\hat \beta\left| {\bf{X}} \right.} \right] = \left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T E\left[ {\varepsilon \varepsilon ^T \left| {\bf{X}} \right.} \right]{\bf{X}}\left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} \end{equation*}\] \[\begin{equation*} Var\left[ {\hat \beta\left| {\bf{X}} \right.} \right] = \left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T \left( {\sigma ^2 {\bf{I}}} \right){\bf{X}}\left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} \end{equation*}\] \[\begin{equation*} Var\left[ {\hat \beta\left| {\bf{X}} \right.} \right] = \sigma ^2 \left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} \end{equation*}\]

Ahora, debemos demostrar que dicha varianza es la mínima posible. Para esto, partamos de escribir de otra manera el estimador MCO \[\begin{equation*} \hat \beta = \left( {{\bf{X}}^{\bf{T}} {\bf{X}}} \right)^{ - 1} {\bf{X}}^{\bf{T}} {\bf{y}} \end{equation*}\] \[\begin{equation*} \hat \beta = {\bf{Ay}} \end{equation*}\] Supongamos ahora que existe otro estimador lineal \[\begin{equation*} \tilde \beta = {\bf{Cy}} \end{equation*}\]

Para ser comparable, el nuevo estimador debe ser insesgado \[\begin{equation*} E\left[ {\tilde \beta \left| {\bf{X}} \right.} \right] = E\left[ {{\bf{Cy}}\left| {\bf{X}} \right.} \right] = {\bf{C}}E\left[ {{\bf{X}}\beta + \varepsilon \left| {\bf{X}} \right.} \right] \end{equation*}\] \[\begin{equation*} E\left[ {\tilde \beta \left| {\bf{X}} \right.} \right] = {\bf{CX}}\beta + {\bf{C}}E\left[ {\varepsilon \left| {\bf{X}} \right.} \right] \end{equation*}\] \[\begin{equation*} E\left[ {\tilde \beta \left| {\bf{X}} \right.} \right] = {\bf{CX}}\beta \end{equation*}\]
Esto quiere decir que para ser insesgado se necesita \[\begin{equation*} {\bf{CX}} = {\bf{I}} \end{equation*}\]
Ahora miremos la varianza, pero antes definamos: \[\begin{equation*} {\bf{D}} = {\bf{C}} - {\bf{A}} = {\bf{C}} - \left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T \end{equation*}\]
Por lo tanto, tenemos que \[\begin{equation*} {\bf{D}}y = \tilde \beta - \hat \beta \end{equation*}\]
y \[\begin{equation*} {\bf{C}} = {\bf{D}} + {\bf{A}} \end{equation*}\]
Entonces, \[\begin{equation*} Var\left[ {\tilde \beta \left| {\bf{X}} \right.} \right] = Var\left[ {\left( {{\bf{D}} + {\bf{A}}} \right){\bf{y}}\left| {\bf{X}} \right.} \right] \end{equation*}\]
\[\begin{equation*} Var\left[ {\tilde \beta \left| {\bf{X}} \right.} \right] = Var\left[ {\left( {{\bf{D}} + {\bf{A}}} \right)\left( {{\bf{X}}\beta + \varepsilon } \right)\left| {\bf{X}} \right.} \right] \end{equation*}\]

Por lo tanto, tenemos que la varianza del otro estimador es \[\begin{equation*} Var\left[ {\tilde \beta \left| {\bf{X}} \right.} \right] = Var\left[ {\left( {{\bf{D}} + {\bf{A}}} \right){\bf{X}}\beta + \left( {{\bf{D}} + {\bf{A}}} \right)\varepsilon \left| {\bf{X}} \right.} \right] \end{equation*}\]
\[\begin{equation*} Var\left[ {\tilde \beta \left| {\bf{X}} \right.} \right] = Var\left[ {\left( {{\bf{D}} + {\bf{A}}} \right)\varepsilon \left| {\bf{X}} \right.} \right] \end{equation*}\] \[\begin{equation*} Var\left[ {\tilde \beta \left| {\bf{X}} \right.} \right] = \left( {{\bf{D}} + {\bf{A}}} \right)Var\left[ {\varepsilon \left| {\bf{X}} \right.} \right]\left( {{\bf{D}} + {\bf{A}}} \right)^T \end{equation*}\] \[\begin{equation*} Var\left[ {\tilde \beta \left| {\bf{X}} \right.} \right] = \left( {{\bf{D}} + {\bf{A}}} \right)\sigma ^2 \left( {{\bf{D}}^T + {\bf{A}}^T } \right) \end{equation*}\] \[\begin{equation*} Var\left[ {\tilde \beta \left| {\bf{X}} \right.} \right] = \sigma ^2 \left( {{\bf{DD}}^T + {\bf{DA}}^T + {\bf{AD}}^T + {\bf{AA}}^T } \right) \end{equation*}\] \[\begin{equation*} Var\left[ {\tilde \beta \left| {\bf{X}} \right.} \right] = \sigma ^2 \left( {{\bf{DD}}^T + {\bf{DX}}\left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} + \left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T {\bf{D}}^T + {\bf{AA}}^T } \right) \end{equation*}\]

Entonces, recordemos que para que \({\tilde{\beta }}\) sea insesgado se necesita \[\begin{equation*} \mathbf{CX}=\mathbf{I} \end{equation*}\] y dado que \[\begin{equation*} \mathbf{C}=\mathbf{D+A} \end{equation*}\]

Esto implica que \[\begin{equation*} \mathbf{CX}=\mathbf{I}=\mathbf{DX+AX} \end{equation*}\]

Por lo tanto \[\begin{equation*} \mathbf{CX}=\mathbf{I}=\mathbf{DX+}{{\left( {{\mathbf{X}}^{T}}\mathbf{X} \right)}^{-1}}{{\mathbf{X}}^{T}}\mathbf{X} \end{equation*}\] \[\begin{equation*} \mathbf{DX}=\mathbf{0} \end{equation*}\]

Regresando a la varianza del estimador, tendremos que:

\[\begin{equation*} Var\left[ {\tilde \beta \left| {\bf{X}} \right.} \right] = \sigma ^2 \left( {{\bf{DD}}^T + {\bf{DX}}\left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} + \left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T {\bf{D}}^T + {\bf{AA}}^T } \right) \end{equation*}\]

\[\begin{equation*} Var\left[ {\tilde \beta \left| {\bf{X}} \right.} \right] = \sigma ^2 \left( {{\bf{DD}}^T + {\bf{AA}}^T } \right) \end{equation*}\] \[\begin{equation*} Var\left[ {\tilde \beta \left| {\bf{X}} \right.} \right] = \sigma ^2 {\bf{DD}}^T + \sigma ^2 \left( {\left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T } \right)\left( {\left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T } \right)^T \end{equation*}\] \[\begin{equation*} Var\left[ {\tilde \beta \left| {\bf{X}} \right.} \right] = \sigma ^2 {\bf{DD}}^T + \sigma ^2 \left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} {\bf{X}}^T {\bf{X}}\left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} \end{equation*}\]

\[\begin{equation*} Var\left[ {\tilde \beta \left| {\bf{X}} \right.} \right] = \sigma ^2 {\bf{DD}}^T + \sigma ^2 \left( {{\bf{X}}^T {\bf{X}}} \right)^{ - 1} \end{equation*}\] \[\begin{equation*} Var\left[ {\tilde \beta \left| {\bf{X}} \right.} \right] = Var\left[ {\hat \beta\left| {\bf{X}} \right.} \right] + \sigma ^2 {\bf{DD}}^T \end{equation*}\] \[\begin{equation*} {\bf{q}}^T {\bf{DD}}^T {\bf{q}} = {\bf{z}}^T {\bf{z}} \geqslant 0 \end{equation*}\] \[\begin{equation*} Var\left[ {\tilde \beta \left| {\bf{X}} \right.} \right] \geqslant Var\left[ {\hat \beta\left| {\bf{X}} \right.} \right] \end{equation*}\] Q.E.D.

Por lo tanto, no es posible obtener un estimador insesgado con una varianza menor, aún en presencia de regresores aleatorios.

8.8.3 Demostración del sesgo del estimador de la regresión de Ridge

Partamos de la definición del estimador de Ridge: \[\begin{equation*} \mathbf{b}\left( l \right)={{\left( {{\mathbf{X}}^{T}}\mathbf{X}+l\mathbf{I} \right)}^{-1}}{{\mathbf{X}}^{T}}y \end{equation*}\]

Ahora calculemos el valor esperado de dicho estimador: \[\begin{equation*} E\left[ {{\mathbf{b}}\left( l \right)\left| {\mathbf{X}} \right.} \right] = E\left[ {\left( {{\mathbf{X}}^T {\mathbf{X}} + l{\mathbf{I}}} \right)^{ - 1} {\mathbf{X}}^T y\left| {\mathbf{X}} \right.} \right] \end{equation*}\] \[\begin{equation*} E\left[ {{\mathbf{b}}\left( l \right)\left| {\mathbf{X}} \right.} \right] = \left( {{\mathbf{X}}^T {\mathbf{X}} + l{\mathbf{I}}} \right)^{ - 1} {\mathbf{X}}^T E\left[ {y\left| {\mathbf{X}} \right.} \right] \end{equation*}\] \[\begin{equation*} E\left[ {{\mathbf{b}}\left( l \right)\left| {\mathbf{X}} \right.} \right] = \left( {{\mathbf{X}}^T {\mathbf{X}} + l{\mathbf{I}}} \right)^{ - 1} {\mathbf{X}}^T E\left[ {{\mathbf{X}}\beta + \varepsilon \left| {\mathbf{X}} \right.} \right] \end{equation*}\] \[\begin{equation*} E\left[ {{\mathbf{b}}\left( l \right)\left| {\mathbf{X}} \right.} \right] = \left( {{\mathbf{X}}^T {\mathbf{X}} + l{\mathbf{I}}} \right)^{ - 1} {\mathbf{X}}^T {\mathbf{X}}\beta \end{equation*}\]
Es fácil ver que el sesgo será mayor si \(l\) es más grande. Por otro lado, es fácil mostrar que la varianza de este estimador es: \[\begin{equation*} Var\left[ {{\mathbf{b}}\left( l \right)\left| {\mathbf{X}} \right.} \right] = \sigma ^2 \left( {{\mathbf{X}}^T {\mathbf{X}} + l{\mathbf{I}}} \right)^{ - 1} {\mathbf{X}}^T {\mathbf{X}}\left( {{\mathbf{X}}^T {\mathbf{X}} + l{\mathbf{I}}} \right)^{ - 1} \end{equation*}\] Así, la varianza del estimador tiende a ser más pequeña entre más grande sea \(l\). De hecho, \(Var\left[ \hat \beta \left| \mathbf{X} \right. \right] > Var\left[ {\mathbf{b} \left( l \right)\left| \mathbf{X} \right.} \right]\)

Referencias

Alonso, J. C. (2020a). Herramientas del Business Analitycs en R: Análisis de Componentes Principales para resumir variables. Economics Lecture Notes, 10, 1–32. https://ideas.repec.org/p/col/000559/018188.html

Auguie, B. (2017). gridExtra: Miscellaneous functions for "grid" graphics. https://CRAN.R-project.org/package=gridExtra

Belsley, D. A., Kuh, E., & Welsch, R. E. (1980). Regression Diagnostics: Identifying Influential Data and Sources of Collinearity. John Wiley & Sons, Inc. https://doi.org/10.1002/0471725153

Bernat, L. F. (2004). Diferencias salariales por género en las siete principales áreas metropolitanas colombianas. ¿Evidencia de discriminación? Investigaciones Sobre Género y Desarrollo En Colombia, 1.

Cule, E., & De Iorio, M. (2012). A semi-automatic method to guide the choice of ridge parameter in ridge regression. arXiv Preprint arXiv:1205.0686, 1–32. http://arxiv.org/abs/1205.0686

Cule, E., Moritz, S., & Frankowski, D. (2021). Ridge: Ridge regression with automatic selection of the penalty parameter. https://CRAN.R-project.org/package=ridge

Fox, J., & Weisberg, S. (2019). An r companion to applied regression (Third). Sage. https://socialsciences.mcmaster.ca/jfox/Books/Companion/

Hair, J. F. J., Black, W. C., Babin, B. J., & Anderson, R. E. (2014). Multivariate Data Analysis (7th ed.). Pearson.

Kutner, M. H.; Nachtsheim, C. J.; Neter, J. (2004). Applied Linear Regression Models (4 th). McGraw-Hill Irwin.

Oaxaca, R. (1973). Male-female wage differentials in urban labor markets. International Economic Review, 14(3), 693–709.

Sheather, S. (2009). A modern approach to regression with r. Springer Science & Business Media.

Wickham, H. (2016). ggplot2: Elegant graphics for data analysis. Springer-Verlag New York. https://ggplot2.tidyverse.org

---

78. Esta relación se representa por el área en común entre el círculo que representa la variable explicativa y la dependiente.↩︎

79. No existe área en común entre las variables explicativas.↩︎

80. En el Capítulo 14 puedes encontrar un repaso de los conceptos de álgebra matricial para entender esta argumentación.↩︎

81. Por simplicidad solo consideraremos cambios en el intercepto.↩︎

82. \(Var\left[ {\hat \beta } \right] = {\sigma ^2}{\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}\).↩︎

83. Recordemos que \(t_c = \frac{{\hat \beta_i }}{{s_{\hat \beta_i } }}\).↩︎

84. Antes de continuar es importante resaltar que la multicolinealidad no perfecta no es un problema del modelo que se estima sino de la muestra con la que se cuenta. Es decir, se puede estimar el mismo modelo, pero con una muestra diferentes y no tener multicolinealidad. Por eso al problema de multicolinealidad se le clasifica como un problema de los datos.↩︎

85. Esto ocurre porque la matriz \({\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}\) cambiaría mucho con incluir o eliminar una fila de \({\bf {X}}\).↩︎

86. En la sección 2.5, se presenta la demostración del teorema de Gauss-Markov. En esta demostración, es fácil notar que las propiedades de insesgadez y mínima varianza de los estimadores MCO dependen de los supuestos asociados al término de error y no a qué tan grande o pequeño sea el determinante de la matriz \(X^{T}X\).↩︎

87. Formalmente, las pruebas disponibles para detectar la multicolinealidad son más unas métricas que sirven como indicador de la presencia del problema. Lo que veremos a continuación no son pruebas en el sentido estricto al no involucrar un estadístico de prueba y una comparación con un valor de una distribución o un valor p asociado a la decisión.↩︎

88. Para la discusión de cómo se calculan los valores propios de una matriz puedes ver la sección 14.10.↩︎

89. En el Anexo de este capítulo, sección 8.8, se presenta una demostración del sesgo que presenta este estimador.↩︎

90. Los datos y la aproximación de esta sección corresponden a Bernat (2004).↩︎

91. Los datos se pueden descargar de la página web del libro: https://www.icesi.edu.co/editorial/modelo-clasico/.↩︎

92. Los datos se pueden descargar de la página web del libro: https://www.icesi.edu.co/editorial/modelo-clasico/.↩︎