15 Elementos de Estadística
Objetivos del capítulo
Al finalizar este capítulo, el lector estará en capacidad de:
- Explicar en sus propias palabras la diferencia entre una variable aleatoria y una no aleatoria.
- Explicar en sus propias palabras los conceptos de: valor esperado, varianza y covarianza.
15.1 Introducción
Este libro supone el conocimiento básico de estadística que le permiten al científico de datos trabajar con grandes volúmenes de datos y modelos estadísticos. Este Apéndice presenta unos conceptos básicos de estadística necesarios para seguir algunas demostraciones y operaciones descritas en el libro. Este Apéndice no pretende ser un tratado autocontenido de estadística, sino por el contrario un breve resumen que permitirá al lector ya familiarizado con los conceptos recordar los concepto.
En general, la Estadística es definida como “la ciencia de estimar la distribución de probabilidad de una variable aleatoria basada en repetidas observaciones de variables aleatorias de la misma variable aleatoria137 (Amemiya, 1994).
Así, la estadística es una ciencia que emplea conjuntos de datos para obtener a partir de ellos inferencias (proyección, adivinanza) sobre una población (valor real). De manera que el problema estadístico consiste en encontrar la mejor predicción para un valor real desconocido para el investigador, a partir de datos recolectados (muestra) de una población.
En este capítulo repasaremos los conceptos básicos de estadística y probabilidad que son las bases para este libro.
15.2 Variables, vectores y matrices aleatorias
Una variable se define como una magnitud que puede tener un valor cualquiera de los comprendidos en un conjunto. En otras palabras, es una “letra” que puede tomar uno o diferentes valores. Por ejemplo, si la variable \(x\) cumple la condición de que \(3x =2\), entonces la variable necesariamente tomará el valor de \(3/2\) (\(x = 3/2\)). Otro ejemplo, si la variable cumple la condición \(x^2 =1\), entonces \(x\) puede tomar los valores de \(1\) o \(-1\).
Ahora, consideremos la definición de una variable aleatoria, también conocida como variable estocástica. Una variable aleatoria es una “letra” que toma diferentes valores, cada uno con una probabilidad previamente definida. Por ejemplo, tiremos una moneda justa al aire, y sea \(X\) la variable aleatoria que toma el valor de uno si la cara superior de la moneda es sello, en caso contrario la variable toma el valor de cero. Es decir: \[\begin{equation*} X=\begin{cases} 1 & \text{ si sello } \\ 0 & \text{ si cara } \end{cases} \end{equation*}\] Entonces, en este caso, diremos que la variable aleatoria \(X\) tiene dos posibles realizaciones. Ahora bien, si la moneda es una moneda normal, existirá igual probabilidad que la variable aleatoria tome el valor de uno o cero. En otras palabras, tendremos que la probabilidad de que la variable aleatoria sea igual a uno es 0.5, al igual que la probabilidad que la variable aleatoria sea cero. Esto se puede abreviar de la siguiente forma: \(P(X=1)=0.5\) y \(P(X=0)=0.5\).
Si el conjunto de valores que toma la variable aleatoria es un conjunto finito o infinito contable, entonces la variable estocástica se denomina una variable aleatoria discreta. Por otro lado, si las posibles realizaciones de la variable aleatoria son un conjunto de realizaciones infinitamente divisible y, por tanto, imposible de contar, entonces la variable estocástica se conoce como una variable aleatoria continua. En general, si las posibles realizaciones toman valores discretos entonces estamos hablando de una variable estocástica discreta; por el contrario, si los posibles valores son parte de un rango continuo de valores, entonces estamos hablando de una variable estocástica continua.
Un vector aleatorio es un vector cuyos elementos son variables aleatorias ya sean continuas o discretas, es decir: \[\begin{equation} \textbf{X}=\begin{bmatrix} X_1\\ X_2\\ \vdots \\ X_n \end{bmatrix} \tag{15.1} \end{equation}\] donde \(X_i\) para \(i = 1, 2, \dots , n\) representan diferentes variables aleatorias. Análogamente, una matriz aleatoria es una matriz cuyos elementos son variables aleatorias.
Es importante anotar que los científicos de datos interpretan la mayoría de los aspectos de la realidad como resultados de un proceso estocástico. En la práctica observamos un único valor de una variable como las ventas mensuales o los rendimientos de un activo. Los valores observados en la realidad para esas variables aleatorias (muestra), se interpretan como las realizaciones de una variable aleatoria después de que los “dados” de la economía o el negocio ya han sido tirados. Es decir, lo que observa el científico de datos es la realización de un evento aleatorio.
15.3 Distribución de probabilidad
Una distribución de probabilidad de una variable aleatoria discreta, también conocida como la función de densidad discreta, \(f(x)\), es una lista de las probabilidades asociadas a las diferentes realizaciones \(x\) que puede tomar una variable aleatoria discreta \(X\). Para una variable aleatoria discreta tenemos que, \[\begin{equation} f(x)=P(X=x) \tag{15.2} \end{equation}\] donde debe cumplir que:
- \(0 \leq f(x)\leq 1\)
- \(\sum_{\forall i} {f(x_i)}\)
Dado que en el caso de una variable aleatoria continua, ésta puede tomar cualquier valor dentro de un número infinito de valores, será imposible asignar una probabilidad para cada uno de los valores que puede tomar la variable aleatoria continua. Por tanto, en el caso de variables aleatorias continuas es necesario un enfoque diferente al seguido con las variables aleatorias discretas. En este caso definiremos una función que nos permita conocer la probabilidad de ocurrencia de un intervalo (conjunto continuo de puntos) y no un punto como lo hicimos para las variables aleatorias discretas.
Una distribución de probabilidad de una variable aleatoria continua, también conocida como la función de densidad continua, \(f(x)\) , es una función asociada a la variable aleatoria continua \(X\), tal que: \[\begin{equation} \int_{a}^{b}{f(x)dx}=P(a \leq x \leq b ) \tag{15.3} \end{equation}\] donde debe cumplir que:
- \(f(x) \geq 0\)
- \(\int_{-\infty }^{\infty}{f(x)dx}=1\)
15.4 Valor esperado de una variable aleatoria
Eventualmente, las distribuciones de probabilidad se pueden describir con sus momentos138. El primer momento de una distribución se conoce como el valor esperado o esperanza matemática.
El valor esperado de una variable aleatoria corresponde a su media poblacional y se interpreta como el valor promedio que se espera de la variable aleatoria cuando se obtiene cualquier muestra de ésta.
El valor esperado de una variable aleatoria discreta denotado por \(E[X]\) se define como: \[\begin{equation} E[X]= \sum_{\forall i} {x_i P(X=x_i)}=\sum_{\forall i} {x_i f(x_i)} \tag{15.4} \end{equation}\]
El valor esperado de una variable aleatoria continua, también denotado por \(E[X]\) se define como: \[\begin{equation} E[X]= \int_{-\infty }^{\infty}{xf(x)dx} \tag{15.5} \end{equation}\] El valor esperado también es conocido como el operador de esperanza matemática, es un operador lineal cuyas principales características son:
- \(E[c]=c\), donde \(c\) es una constante, o una variable no estocástica.
- \(E[aX + b]= a E[X] + b\), donde \(a\) y \(b\) son constantes y \(X\) es una variable aleatoria.
- En general \(E[g(X)] \neq g(E(X))\), donde \(g(\cdot)\) es cualquier función. La única excepción de esto es cuando \(g(\cdot)\) es una función lineal.
- \(E[a_1 X_1 + a_2 X_2 + \dots + a_n X_n ]= a_1 E[X_1] + a_2 E[X_2] + \dots + a_n E[X_n]\) donde cada uno de los \(a_i\) y \(X_i\) (\(i = 1, 2, \cdots, n\)) son constantes y variables aleatorias, respectivamente.
- \[X = \begin{cases} \sum_{\forall i} {g(x) f(x_i)}& \text{ si X es discreta } \\ \int_{-\infty }^{\infty}{g(x)f(x)dx} & \text{ Si X es cont.} \end{cases} \]
Como se mencionó anteriormente, \(E[x]\) se conoce como el primer momento de una variable aleatoria y también se denota como \(\mu_x\). Es decir, la media poblacional de \(X\). El i-ésimo momento (alrededor del origen) de una variable aleatoria \(X\) está definido por \({\mu}'_i = E[X^i]\).
15.5 Independencia (estadística) lineal
Dos variables aleatorias, \(X\) y \(Y\), se consideran estadísticamente independientes, u ortogonales, si y solamente si: \[\begin{equation} E[XY]= E[X]E[Y] \tag{15.6} \end{equation}\]
Es importante notar que independencia estadística entre dos variables no implica que no exista relación alguna entre las variables, como se verá más adelante, independencia estadística sólo implica que no existe una relación lineal entre las dos variables.
15.6 Varianza y momentos alrededor de la media de una variable aleatoria
La varianza de una variable aleatoria, denotada por \(\sigma ^2\) o \(Var[X]\) , se define como: \[\begin{equation} Var\left [ X \right ]= E\left [ \left ( x- \mu \right )^2\right ] \tag{15.7} \end{equation}\] Así, en el caso de una variable aleatoria discreta tendremos que: \[\begin{equation*} Var\left [ X \right ]= \sum_{\forall i} { \left ( x- \mu \right )^2 f(x_i)}, \end{equation*}\] y para una variable estocástica continua la varianza será calculada de la siguiente manera: \[\begin{equation*} Var\left [ X \right ]= \int_{-\infty }^{\infty}{\left ( x- \mu \right )^2f(x)dx}. \end{equation*}\] La varianza es una medida de la dispersión de una distribución. Generalmente se emplea la raíz cuadrada de la varianza, la desviación estándar (\(\sigma = \sqrt[+] {Var\left [ X \right ]}\)), para describir una distribución. La ventaja de la desviación estándar es que ésta está medida en las mismas unidades de \(X\) y \(\mu\).
Un ejemplo de cómo la desviación estándar puede ser empleada para describir la dispersión de una distribución está dado por la desigualdad de Chebychev; para cualquier variable aleatoria y para cualquier constante se tiene que: \[\begin{equation} P\left ( \mu - k\sigma \leq x \leq \mu + k\sigma \right )\geq 1 - \frac{1}{k^2} \tag{15.8} \end{equation}\]
Antes de continuar, es importante anotar que el cálculo directo de la varianza es relativamente engorroso, afortunadamente es fácil mostrar que: \[\begin{equation} Var\left [ X \right ]= E\left [ X^2 \right ]-\left ( E\left [ X \right ] \right )^2 \tag{15.9} \end{equation}\] este resultado permite en la práctica agilizar el cálculo de la varianza de cualquier variable aleatoria.
Las principales propiedades de la varianza son:
\(Var\left [ c \right ]=0\), donde \(c\) es una constante, o una variable no estocástica.
\(Var\left [ aX + b \right ]= a^2 Var\left [ X \right]\), donde \(a\) y \(b\) son constantes y \(X\) es una variable aleatoria.
\(Var\left [ aX + b Y \right ] = a^2 Var\left [ X \right ] + b^2 Var\left [ Y \right ] + 2a b Cov\left [ X, Y \right ]\) donde \(a\) y \(b\) son constantes y \(X\) y \(Y\) son variables aleatorias, respectivamente (en la próxima sección repasaremos el concepto de covarianza (\(Cov\left [ X, Y \right ]\))).
La varianza de una variable aleatoria también es conocida como el segundo momento alrededor de la media. En general, el i-ésimo momento alrededor de la media de una variable aleatoria se define como: \[\begin{equation} \mu_i =E\left [ \left ( x- \mu \right )^i\right ] \tag{15.10} \end{equation}\]
El tercero y cuarto momento alrededor de la media se conocen como la asimetría ( en inglés) y curtosis, respectivamente. Una medida de asimetría comúnmente empleada es el coeficiente de asimetría definido como: \[\begin{equation} A=\frac{\mu_3}{\sigma^3} \tag{15.11} \end{equation}\]
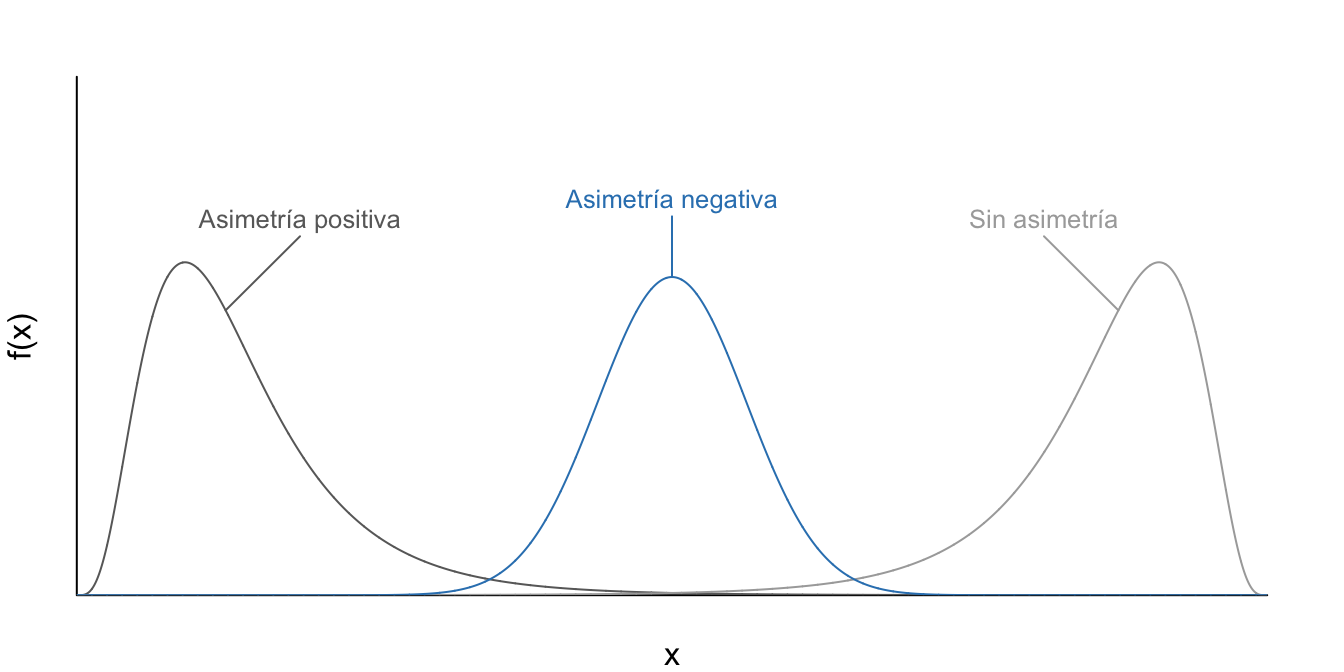
En la Figura 15.1 se presentan los posibles casos extremos para interpretar el coeficiente de asimetría. En general, cuando ambas colas de la distribución tienen igual longitud, diremos que la distribución es simétrica o no posee asimetría. Por otro lado, si la cola izquierda (derecha) es más ``corta’’ (larga) que la derecha, entonces la distribución se dirá que la distribución tiene asimetría positiva (negativa) (Ver Figura 15.1). En algunos casos la asimetría positiva también se conoce como asimetría a la derecha, mientras que la asimetría negativa se denomina asimetría a la izquierda.
Figura 15.1: Tipos de Asimetría de diferentes distribuciones
Otro estadístico comúnmente empleado para describir que tan “aplanada” o “picuda” es una distribución, es el coeficiente de curtosis que se define como: \[\begin{equation} C=\frac{\mu_4}{\sigma^4} \tag{15.12} \end{equation}\]
Para efectos de comparación, se emplea como distribución referente la distribución normal. Una distribución que es relativamente más picuda que una distribución normal se le denomina leptocúrtica. Contrariamente, aquella distribución más plana que la distribución normal se le denomina platicúrtica (Ver Figura 15.2).
Figura 15.2: Tipos de Curtosis de diferentes distribuciones

15.7 Covarianza y Correlación entre dos variables aleatorias
Ahora consideremos la covarianza entre dos variables aleatorias \(X\) y \(Y\) denotada por \(Cov\left [ X, Y \right ]\) ó \(\sigma_{x,y}\) y definida como: \[\begin{equation} Cov\left [ X, Y \right ]= E\left [ \left ( X-E\left [ X \right ] \right ) \left ( Y -E\left [ Y \right ] \right )\right ] \tag{15.13} \end{equation}\] Al igual que lo que ocurre con la varianza de una variable aleatoria, el cálculo directo de una covarianza es muy engorroso. Afortunadamente, es fácil mostrar que: \[\begin{equation} Cov\left [ X, Y \right ]= E\left [ XY\right ]-E\left [ X\right ]E\left [ Y\right ] \tag{15.14} \end{equation}\]
La expresión (15.14) ayuda a entender la utilidad de la covarianza entre dos variables aleatorias. Noten que en caso de que las variables estocásticas \(X\) y \(Y\) sean independientes, se tendrá por definición que \(E[XY]= E[X]E[Y]\). Y por tanto,\(Cov\left [ X, Y \right ]= 0\).
De esta manera, la covarianza entre dos variables aleatorias será cero si no existe relación lineal (hay independencia) entre ellas; y será diferente de cero si no hay independencia estadística entre ellas. Por otro lado, en el caso de que al mismo tiempo que una realización de la variable aleatoria \(X\) está por encima de su media, la realización de la variable estocástica \(Y\) también está por encima de su media, entonces la covarianza de estas dos variables será positiva. Si cuando la realización de una variable aleatoria está por encima de su media la realización de la otra variable está por debajo de la media, entonces la covarianza será negativa.
Una importante propiedad de la covarianza es: \[\begin{equation*} Cov\left [ a+bX, c+dY \right ]= bdCov\left [ X, Y \right ], \end{equation*}\] donde \(a\), \(b\), \(c\) y \(d\) son constantes, y \(X\) y \(Y\) son variables aleatorias.
Como se mencionó anteriormente, la covarianza entre dos variables estocásticas mide la relación lineal entre las variables, pero ésta depende de las unidades en que están medidas \(X\) y \(Y\). Para tener una medida del grado de dependencia lineal entre dos variables aleatorias, que no dependa de las unidades, se emplea el coeficiente de correlación.
La correlación entre dos variables aleatorias, denotado por \(\rho\), está definida por: \[\begin{equation} \rho= \frac{Cov\left [ X, Y \right ]}{\sqrt{Var\left [ X \right ]}\sqrt{Var\left [ Y \right ]}} \tag{15.15} \end{equation}\]
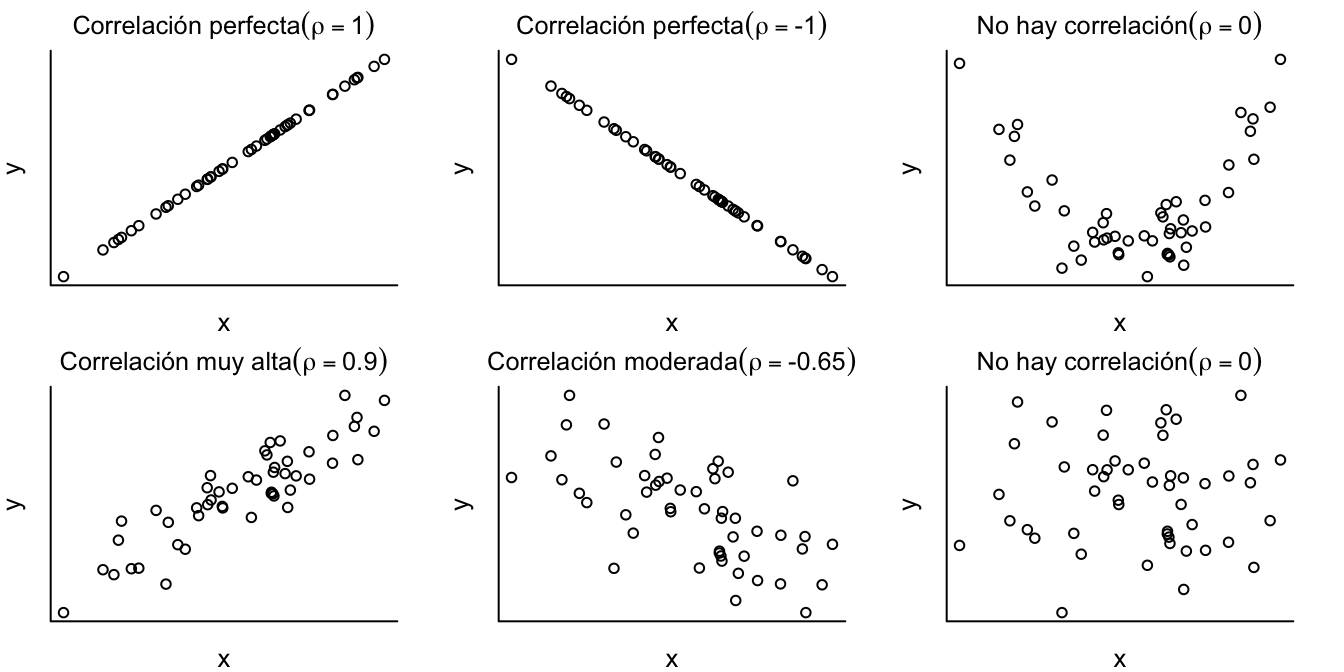
Es muy fácil mostrar que \(-1\leq \rho \leq 1\). La correlación entre dos variables aleatorias tiene una interpretación muy sencilla; por ejemplo, una correlación de 1/-1 entre las variables aleatorias \(X\) y \(Y\) implica una relación lineal positiva/negativa y perfecta entre ellas. Mientras que una correlación de cero implica que no existe relación lineal entre las variables. En la Figura 15.3.
Figura 15.3: Ejemplos de diferentes valores de la correlación
15.8 Esperanza y Varianza de vectores aleatorios.
Como se mencionó anteriormente, un vector aleatorio es un vector cuyos elementos son todos variables aleatorias. Así, el valor esperado de un vector aleatorio corresponde a un vector cuyos elementos son los valores esperados de los correspondientes elementos del vector estocástico. En otras palabras, sea \(\textbf{X}\) un vector aleatorio, entonces: \[\begin{equation} E\left [ \textbf{X} \right ]= E\left [ \begin{bmatrix} X_1\\ X_2\\ \vdots \\ X_n \end{bmatrix} \right ]= \begin{bmatrix} E\left [ X_1 \right ]\\ E\left [ X_2 \right ]\\ \vdots \\ E\left [ X_n \right ] \end{bmatrix}=\begin{bmatrix} \mu_1 \\ \mu_2 \\ \vdots \\ \mu_n \end{bmatrix}=\mu_{n \times 1} \tag{15.16} \end{equation}\]
Es muy fácil extender esta idea para encontrar el valor esperado de una matriz aleatoria. Sea \(\textbf{X}_{n \times m}\) una matriz aleatoria de dimensiones \(n \times m\), entonces: \[\begin{equation} E\left [ \textbf{X}_{n \times m} \right ]= \begin{bmatrix} E\left [ X_{11} \right ]& E\left [ X_{12} \right ]& \dots & E\left [ X_{1m} \right ] \\ E\left [ X_{21} \right ]& E\left [ X_{22} \right ]& \dots & E\left [ X_{2m} \right ]\\ \vdots & \vdots & \vdots & \vdots\\ E\left [ X_{n1} \right ] &E\left [ X_{n2} \right ] & \dots & E\left [ X_{nm} \right ] \end{bmatrix} \tag{15.17} \end{equation}\]
Análogamente al caso de una variable aleatoria, la varianza de un vector aleatorio \(\textbf{X}_{n \times 1}\) se define como: \[\begin{equation} Var\left [ \textbf{X}_{n \times 1} \right ]=E \left [ \left ( \textbf{X}_{n \times 1} - \mu\right ) \left ( \textbf{X}_{n \times 1} - \mu\right )^T \right ]=E \left [ \textbf{X}_{n \times 1} \textbf{X}_{n \times 1}^T \right ]-\mu \mu^T \tag{15.18} \end{equation}\] En este caso tenemos que: \[\begin{equation} Var\left [ \textbf{X}_{n \times 1} \right ]=\begin{bmatrix} E \left [ \left ( X_1 - \mu_1 \right ) \left ( X_1 - \mu_1 \right )\right ]& E\left[ \left ( X_1 - \mu_1 \right ) \left ( X_2 - \mu_2 \right )\right ]& \dots & E\left [ \left ( X_1 - \mu_1 \right ) \left ( X_n - \mu_n \right )\right ] \\ E\left [ \left ( X_2 - \mu_2 \right ) \left ( X_1 - \mu_1 \right ) \right ]& E\left [ \left ( X_2 - \mu_2 \right ) \left ( X_2 - \mu_2 \right ) \right ]& \dots & E\left [ \left ( X_2 - \mu_2 \right ) \left ( X_n - \mu_n \right )\right ]\\ \vdots & \vdots & \vdots & \vdots\\ E\left [ \left ( X_n - \mu_n \right ) \left ( X_1 - \mu_1 \right ) \right ] &E\left [ \left ( X_n - \mu_n \right ) \left ( X_2 - \mu_2 \right ) \right ] & \dots & E\left [ \left ( X_n - \mu_n \right ) \left ( X_n - \mu_n \right ) \right ] \end{bmatrix} \tag{15.19} \end{equation}\] La matriz de varianzas de un vector aleatorio \(\textbf{X}_{n \times 1}\), conocida como la matriz de covarianzas o la matriz de varianzas y covarianzas, está dada por: \[\begin{equation} Var\left [ \textbf{X}_{n \times 1} \right ]=\begin{bmatrix} Var \left [ X_1 \right ]& Cov\left[ X_1, X_2 \right]& \dots & Cov\left[ X_1, X_n \right] \\ Cov\left[ X_2, X_1 \right]& Var \left [ X_2 \right ]& \dots & Cov\left[ X_2 X_n \right]\\ \vdots & \vdots & \vdots & \vdots\\ Cov\left[ X_n, X_1 \right] & Cov\left[ X_n, X_2 \right] & \dots & Var \left [ X_n \right ] \end{bmatrix} \tag{15.20} \end{equation}\]
En algunas ocasiones esta matriz se escribe de la siguiente manera: \[\begin{equation} Var\left [ \textbf{X}_{n \times 1} \right ]=\begin{bmatrix} \sigma_1 ^2& \sigma_{12}& \dots & \sigma_{1n} \\ \sigma_{21}& \sigma_2 ^2& \dots & \sigma_{2n}\\ \vdots & \vdots & \vdots & \vdots\\ \sigma_{n1} & \sigma_{n2} & \dots & \sigma_n ^2 \end{bmatrix}=\Sigma \tag{15.21} \end{equation}\] Nota que esta matriz es simétrica pues en general \(\sigma_{ij}= \sigma_{ji}\).
Dividiendo cada uno de los \(\sigma_{ij}\) por las respectivas \(\sigma_{i}\) y \(\sigma_{j}\) obtendremos la matriz de correlaciones: \[\begin{equation} \begin{bmatrix} 12& \rho_{12}& \dots & \rho_{1n} \\ \rho_{21}&1& \dots & \rho_{2n}\\ \vdots & \vdots & \vdots & \vdots\\ \rho_{n1} & \rho_{n2} & \dots & 1 \end{bmatrix} \tag{15.22} \end{equation}\]
Antes de continuar, consideremos las siguientes propiedades. Sean \(\textbf{a}\) un vector de constantes, \(\textbf{A}\) una matriz de constantes y \(\textbf{X}_{n \times 1}\) un vector aleatorio, entonces:
- \(E\left [\textbf{a}^T \textbf{X} \right ]= \textbf{a}^T\mu\)
- \(Var\left [\textbf{a}^T \textbf{X} \right ]= \textbf{a}^TVar\left [ \textbf{X} \right ]\textbf{a}= \textbf{a}^T\Sigma\textbf{a}\)
- \(E\left [\textbf{A} \textbf{X} \right ]= \textbf{A}\mu\)
- \(Var\left [\textbf{A} \textbf{X} \right ]= \textbf{A}\Sigma\textbf{a} \textbf{A}^T\)
- \(E\left [ tr( \textbf{X}_{n \times n}) \right ]= tr\left ( E\left [ \textbf{X}_{n \times n} \right ] \right )\)
15.9 Estimadores puntuales y sus propiedades deseadas
Intuitivamente, un estimador se puede entender como una “fórmula” que permite pronosticar un valor poblacional (parámetro) desconocido a partir de una muestra. Por ejemplo, supongamos que deseamos conocer la media de una población. Regularmente no conocemos este valor y, por tanto, se recolectan observaciones de parte de la población total (muestra), y a partir de estas observaciones evaluamos una fórmula para conocer nuestro pronóstico del valor poblacional real.
Formalmente un estimador, también conocido como estimador puntual, de un parámetro poblacional es una función que indica cómo calcular una matriz, vector o escalar a partir de una muestra. El valor arrojado por esta función una vez los valores muestrales son reemplazados en el estimador se denomina estimación.
Así, un estimador \(\hat \theta\) para pronosticar un parámetro \(\theta\) a partir de una muestra aleatoria de tamaño \(n\) se define como: \[\begin{equation} \hat \theta= h\left ( X_1, X_2, \dots, X_n \right ) \tag{15.23} \end{equation}\] donde \(h\left ( \cdot \right )\) es una función cualquiera y \(X_1, X_2, \dots, X_n\) corresponden a cada uno de los puntos muestrales (elementos de la muestra). Los estimadores son variables aleatorias, pues son función de variables aleatorias.
Claramente cualquier función de los puntos muestrales por definición es un estimador. Pero, ¿cómo escoger cuál función de la muestra es un buen estimador para el parámetro deseado? Existen varias propiedades deseadas en los estimadores que discutiremos a continuación.
Una propiedad muy deseable es que el valor esperado de la distribución del estimador esté lo más cercano o coincida con el valor población del parámetro. De esta forma, cada vez que se analice información nueva se estará seguro que en promedio el estimador estará correcto. En general, diremos que un estimador es insesgado si \(E\left [ \hat \theta \right ]= \theta\). Así definiremos el sesgo de un estimador como: \[\begin{equation} Sesgo\left [ \hat \theta \right ]= E\left [ \hat \theta \right ]-\theta \tag{15.24} \end{equation}\] La insesgadez es una propiedad deseable en un estimador, pero la ausencia de sesgo no dice nada sobre la dispersión que tiene el estimador alrededor de su media. En general, se preferirá un estimador que tenga una menor dispersión alrededor de la media (varianza) a uno con mayor dispersión. Un estimador \(\hat \theta_1\) es considerado un estimador insesgado más eficiente si: \[\begin{equation} Var\left [ \hat \theta_1 \right ]< Var\left [ \hat \theta_2 \right ] \tag{15.25} \end{equation}\]
Ahora consideremos el caso en que estamos comparando un estimador sesgado con una varianza relativamente pequeña con un estimador insesgado con una varianza relativamente grande. La pregunta es: ¿cuál de los dos estimadores deberá ser preferido? Un criterio para escoger un estimador entre otros, es considerar el estimador con el Mínimo Error Medio al Cuadrado, denotado MSE por su nombre en inglés (Mean Square Error), éste se define como: \[\begin{equation} MSE\left [ \hat \theta \right ]= \left ( E\left [ \hat \theta- \theta \right ] \right )^2 \tag{15.26} \end{equation}\] Es fácil mostrar que: \[\begin{equation} MSE\left [ \hat \theta \right ]= \left ( Sesgo\left [ \hat \theta \right ] \right )^2 + Var \left [ \hat \theta \right ] \tag{15.27} \end{equation}\] Así al minimizar el MSE, se está teniendo en cuenta tanto el sesgo como la dispersión del estimador.
Finalmente, otra propiedad deseada en un estimador es la consistencia. Intuitivamente, un estimador es consistente si cuando la muestra se hace grande y más cercana a la población total, entonces la probabilidad de que el estimador \(\hat \theta\) sea diferente del valor poblacional \(\theta\) es cero. Formalmente, \(\hat \theta\) es un estimador consistente si \[\begin{equation} \underset{n \to \infty } {\lim}P\left ( \left | \theta - \hat \theta \right | < \delta \right )=1 \tag{15.28} \end{equation}\] donde \(\delta\) es una constante positiva arbitrariamente pequeña.
Referencias
Este apéndice corresponde a una versión adaptada de Alonso (2007).↩︎
Los momentos de una distribución son representados por parámetros poblacionales que se representarán de aquí en adelante con letras griegas. Los momentos de una distribución describen las características de la distribución poblacional de la variable aleatoria.↩︎