2 Evaluación de los modelos de clasificación

Objetivos del capítulo

Al finalizar este capítulo, el lector estará en capacidad de:

• Explicar en sus propias palabras cuáles son las métricas para determinar la bondad de ajuste de un modelo de clasificación.
• Explicar en sus propias palabras qué es la validación cruzada, para qué sirve y cuándo se debe emplear.
• Efectuar en R una validación cruzada por los métodos de retención, LOOCV y k-folds para seleccionar un modelo de regresión para hacer analítica predictiva (en muestras de corte transversal).

2.1 Introducción

Siempre que se estima o entrena un modelo¹² surge la pregunta ¿qué tan bueno es el modelo?.

Cuando estamos trabajando con modelos cuya variable a explicar (variable objetivo) es cuantitativa (continua o discreta), la forma tradicional de medir qué tan bueno es un modelo es emplear la distancia entre el valor realmente observado y el valor “predicho” por el modelo; i.e., el error del modelo. En este ambiente es común emplear métricas como el RMSE o el \(R^2\), como se realiza en la regresión múltiple o los modelos de series de tiempo.

Pero, cuando la variable a explicar (variable dependiente) es una variable categórica no tiene mucho sentido calcular un error y, por tanto, métricas como el RMSE o el \(R^2\). Por ejemplo, supongamos que estamos hablando de un modelo que se estima o entrena para responder la pregunta ¿cuáles de los clientes pagarán la factura de la tarjeta de crédito a tiempo? En este caso la variable a explicar solo toma dos valores: paga y no paga. Si el modelo estimado o entrenado predice que un individuo pagará y en efecto esa persona no paga, en este caso tendremos un error, pero es imposible determinar la distancia entre el valor predicho y el valor realmente observado. Así, necesitaremos otro tipo de herramientas para determinar si un modelo es bueno o no. En este Capítulo nos concentraremos en algunas métricas de evaluación bastantes usadas en este campo y en discutir cómo se emplean para realizar validación cruzada de los modelos.

2.2 Estrategias para la validación cruzada de modelos

(Esta sección es una versión ligeramente modificada del capítulo 12 de Alonso (2024)).

Antes de entrar en la discusión de las métricas que se emplearán para decidir si un modelo es mejor que otro, es importante reconocer que independientemente de las métricas que se empleen para medir la bondad de ajuste de un modelo, éstas nos llevan a encontrar modelos que explican lo mejor posible la muestra bajo estudio, pero no necesariamente nuevas muestras que aparezcan. Es decir, es posible que tengamos un modelo muy bueno para explicar la muestra (analítica diagnóstica) pero no necesariamente para hacer analítica predictiva. Esto se conoce como el problema de overfitting (sobreajuste).

Cuando los científicos de datos están interesados en responder una pregunta de negocio que involucra emplear analítica predictiva, será necesario evaluar el poder predictivo del modelo. Es importante reconocer que la tarea de clasificación típicamente implica querer predecir la categoría de un individuo (analítica predictiva). Cuando queremos un buen modelo para predecir, queremos evitar el overfitting porque podemos estar dando demasiado poder predictivo a peculiaridades específicas de la muestra que se empleó para estimar el modelo. Pero al mismo tiempo, queremos evitar tener un modelo con bajo ajuste a la muestra (infraajuste o underfitting en inglés) porque estaríamos ignorando patrones en la muestra útiles para determinar el comportamiento de un nuevo individuo.

Para evitar overfitting (sobreajuste) una buena práctica es emplear muestras diferentes para estimar y evaluar la capacidad predictiva de este. En general, cualquier técnica de validación cruzada de modelos implicará dividir la muestra en una muestra de evaluación que sea diferente a la muestra de estimación o también conocida como la muestra de entrenamiento. A esta práctica se le conoce como validación cruzada o en inglés cross-validation¹³.

En general, para realizar la valoración del poder predictivo de varios modelos candidatos empleando la muestra disponible será necesario contar con:

1. una muestra de evaluación que sea diferente a la muestra de estimación o también conocida como la muestra de entrenamiento y
2. una métrica que permita determinar qué tan “precisas” son las predicciones de los modelos.

A continuación, discutiremos tres estrategias de validación cruzada comúnmente empleadas en la práctica por los científicos de datos.

2.2.1 Método de retención

La técnica de validación cruzada más sencilla implica seleccionar aleatoriamente unas observaciones de la muestra para hacer la estimación (muestra de estimación o muestra de entrenamiento) y otra para evaluar el comportamiento del modelo para predecir (muestra de evaluación). Esta técnica es conocida como el método de retención o holdout method.

En este caso, una parte relativamente pequeña de la muestra es seleccionada al azar¹⁴ como muestra de evaluación y la muestra restante es la de estimación. Es común que se emplee el 80% de la muestra para la estimación y el 20% restante para realizar la evaluación. En la Figura 2.1 se presenta un diagrama de esta aproximación. Con la muestra de evaluación se comparan los diferentes modelos de regresión candidatos a ser el mejor modelo para predecir las observaciones. La comparación implica calcular diferentes métricas que discutiremos en la siguiente sección de este capítulo.

Una desventaja de esta aproximación es que la selección del mejor modelo para predecir podría estar determinada por el azar, pues la muestra seleccionada para la evaluación es totalmente aleatoria. Así, si se replicara el ejercicio con otra muestra, el mejor modelo seleccionado podría ser diferente.

Figura 2.1: Diagrama del Método de retención para la evaluación cruzada de modelos

Fuente: elaboración propia.

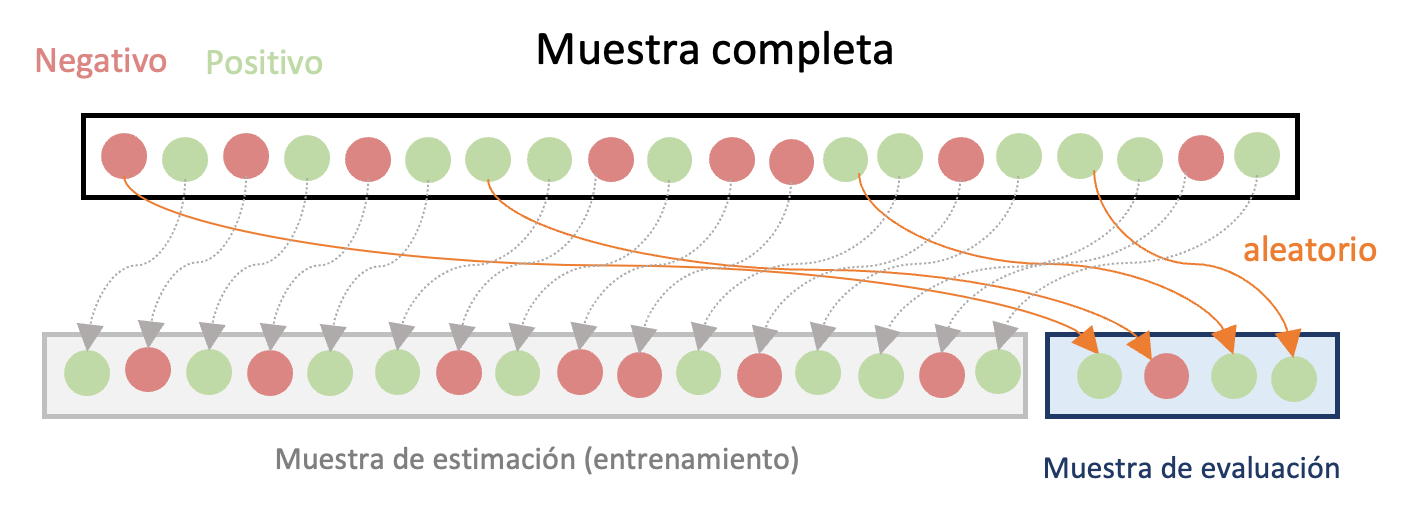
Antes de continuar con otras aproximaciones de validación cruzada de modelos, definamos unos términos importantes en esta literatura. El error del modelo en la muestra de estimación se conoce como el error de entrenamiento. El error del modelo en la muestra de evaluación se conoce como el error de prueba.

2.2.2 Método LOOCV

Otro método de valoración cruzada comúnmente empleado es el denominado LOOCV (por la sigla en inglés del término Leave one out Cross-validation). En este método, a diferencia del método de retención, no se emplea una única muestra de evaluación elegida al azar. Este método implica realizar la estimación y la valoración del modelo en diferentes muestras.

En este caso, se fija una observación en la muestra de evaluación y se estima el modelo con el resto de observaciones (\(n-1\)). Este proceso se repite hasta que todas las observaciones de la muestra han sido empleadas en una muestra de evaluación. En la Figura 2.2 se presenta un diagrama de esta aproximación. Los modelos candidatos se comparan empleando el promedio de las métricas deseadas para evaluar las predicciones para cada una de las \(n\) muestras de evaluación.

Figura 2.2: Diagrama del Método de validación cruzada de LOOCV para la evaluación de modelos

Fuente: elaboración propia.

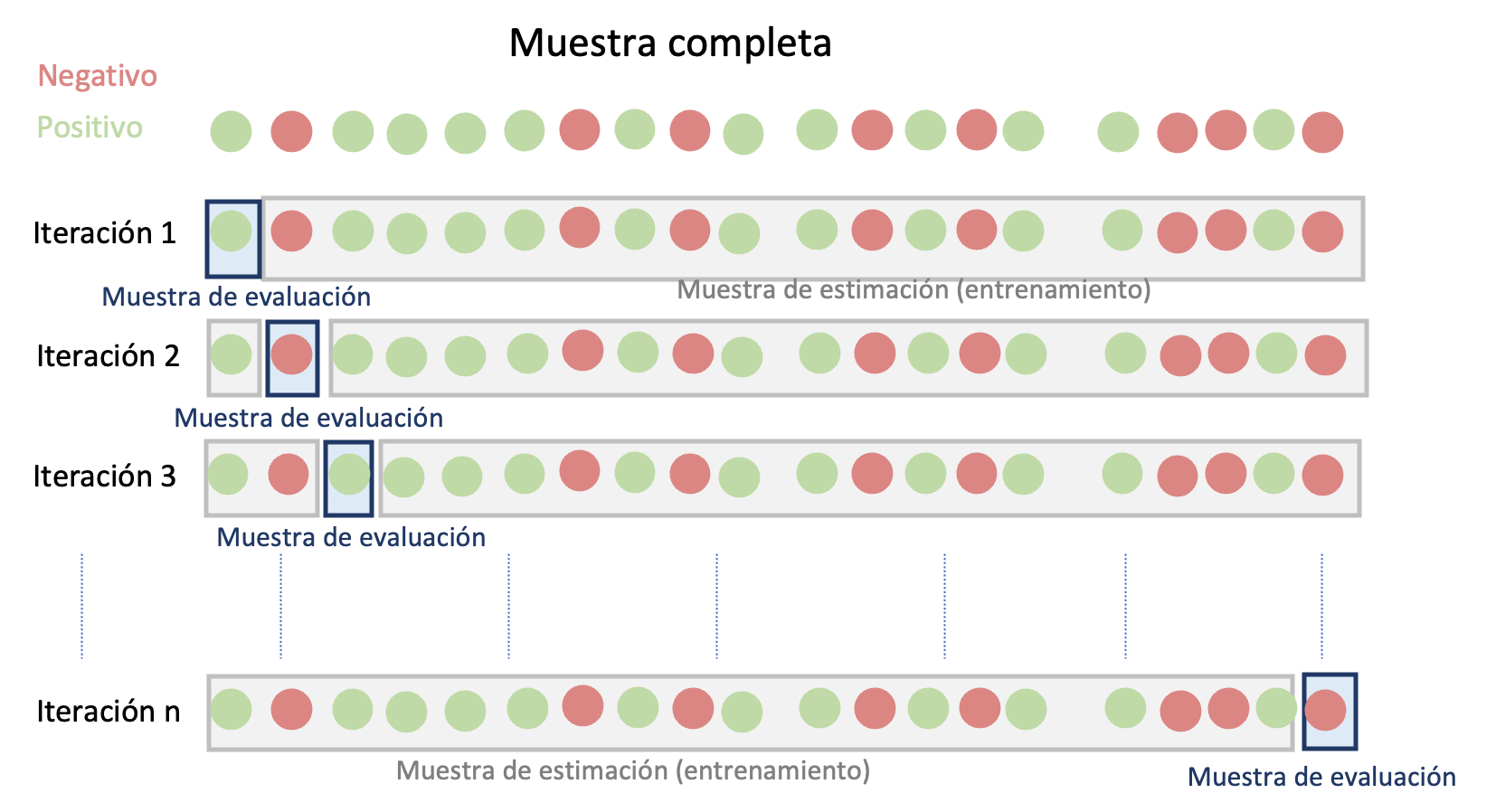
A priori el método LOOCV parecería ser el ideal al emplear todas las observaciones como muestra de evaluación. Esto claramente eliminaría el problema de la aleatoriedad que genera el método de retención al momento de seleccionar el mejor modelo para predecir. No obstante, este método puede ser costoso computacionalmente pues requiere estimar el modelo \(n\) veces.

2.2.3 Método de k iteraciones

A parte del costo computacional del método LOOCV, puede existir potencialmente otro problema con esa aproximación. El LOOCV puede generar una mayor variación en el error de predicción si algunas observaciones son atípicas. Para evitar este problema, lo ideal sería utilizar una buena proporción de observaciones como muestra de prueba para evitar el peso de las observaciones atípicas.

El método de validación cruzada de \(k\) iteraciones o k-fold Cross-validation intenta ser un intermedio entre el método de retención y el LOOCV. Este método implica dividir de manera aleatoria la muestra completa en \(k grupos\) de aproximadamente el mismo tamaño. Para cada uno de los \(k\) grupos (o iteraciones) se emplean los restantes \(k-1\) grupos como muestra de estimación y el grupo \(k\) de observaciones se emplea como muestra de evaluación para la cual se calculan las respectivas métricas deseadas para los modelos a comparar. Y finalmente, para obtener la métrica para todo el ejercicio se calcula el promedio de las \(k\) métricas calculadas para cada modelo. En la Figura 2.3 se presenta un diagrama de esta aproximación. Lo más común en la práctica es emplear un valor de \(k\) de 5 o 10.

Figura 2.3: Diagrama del Método de validación cruzada de \(k\) iteraciones para la evaluación de modelos

Fuente: elaboración propia.

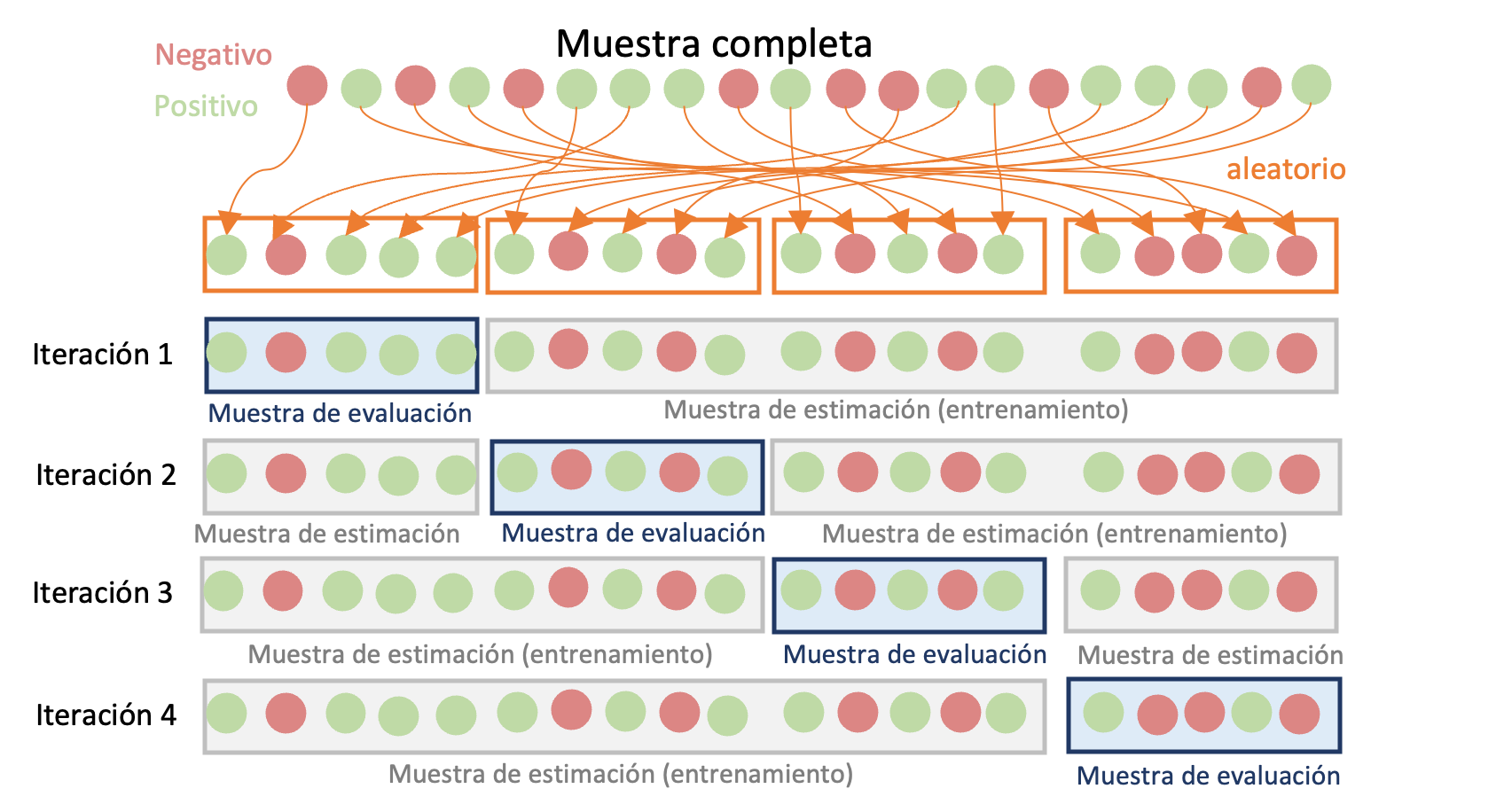
En la práctica, la validación cruzada de \(k\) iteraciones se recomienda generalmente sobre los otros dos métodos debido a su equilibrio entre la variabilidad que puede aparecer por los datos atípicos (método LOOCV), el sesgo fruto de emplear sólo una muestra de evaluación (método de retención) y el tiempo de ejecución computacional. En el Capítulo 10 se presenta una aplicación de este método de validación cruzada.

En la siguiente sección discutiremos las métricas para valorar la precisión de las predicciones.

2.3 Medidas de ajuste de los modelos de clasificación

Evaluar el desempeño de un modelo de clasificación no es una tarea trivial. En este caso, construir un error como la diferencia entre el valor que el modelo espera y el que realmente se observa no es viable, como si lo es en la tarea de regresión o de proyectar.

En los modelos de regresión y pronósticos típicamente se guarda una parte de la muestra (muestra de evaluación) para determinar si el modelo que ha sido entrenado (estimado) en la muestra de entrenamiento (de estimación) tiene un buen comportamiento en ésta. Es decir, se emplea una muestra de entrenamiento para estimar el modelo. Y posteriormente los modelos candidatos son comparados en la muestra de evaluación con una medida de qué tan “cerca” están las predicciones del modelo en la muestra de evaluación. Es decir, se emplean medidas de la distancia (error) entre el valor observado y el valor esperado por el modelo. Entre más pequeña se la medida del error que se emplea, mejor será el modelo. Esto siempre será posible con este tipo de modelos que implican un aprendizaje supervisado sobre variables cuantitativas.

Lastimosamente, en la tarea de clasificación esto no es posible. Dado que las observaciones de la variable objetivo solo corresponden a dos (o un número reducido) de categorías. Así, en este caso calcular la distancia entre la predicción de la categoría y la categoría observada no tiene sentido. Pues en el mundo de las variables cualitativas (que representan las categorías) no tiene sentido restar dos números.

Por eso, es necesario tener una aproximación diferente para determinar qué modelo es mejor para una determinada muestra, independientemente de la estrategia de validación cruzada que empleemos. Los modelos de clasificación producen dos tipos de predicciones. Unos modelos producen como predicción la probabilidad de que ocurra una clase (por ejemplo, el modelo Logit que estudiaremos en el Capítulo 3. Para estos modelos se requiere un paso intermedio para pasar de la probabilidad de que ocurra una determinada categoría a la predicción de la categoría. En estos casos, se establece un valor de corte o umbral (en inglés Cutoff Value o Treshold Value) para determinar a partir de qué valor de la probabilidad estimada se asignará la predicción a una categoría. Para este tipo de modelos se deben tener unas consideraciones especiales que discutiremos en la Sección 2.3.1. Posteriormente discutiremos las métricas que se pueden emplear una vez se cuenta con la predicción de la categoría de los individuos.

2.3.1 Consideraciones para los modelos de clasificación que generan probabilidades

Como se discutirá a lo largo de este libro, algunos de los modelos o algoritmos de clasificación no generan directamente una predicción de la categoría de un individuo, sino la probabilidad (condicionada a las características de este) de que un individuo pertenezca a una categoría determinada. Para este tipo de modelos tenemos que tener en cuenta unas consideraciones especiales a diferencia de los algoritmos que generan directamente las predicciones de la categoría.

De esta manera para los modelos que generan una probabilidad de pertenecer a una categoría, tendremos que construir una forma para decidir a partir de qué probabilidad clasificaremos a un individuo como perteneciente a una categoría o no.

Partamos del modelo más sencillo, donde queremos clasificar solo en 2 categorías, positivos y negativos¹⁵. Es decir, nuestra variable objetivo (\(y_i\)) puede tomar dos valores: positivo (\(y_i\)=1) o negativo (\(y_i\)=0). Los diferentes modelos nos darán la probabilidad de que observemos un valor positivo ( \(y_i = 1\)). Entonces, para determinar el valor estimado del modelo para \(y_i\) (\(\hat{y}_i\)) tendremos que definir un valor de corte¹⁶ \(\lambda\) para determinar a partir de qué valor de la probabilidad estimada se entenderá que \(\hat{y}_i\) tomará el valor de uno.

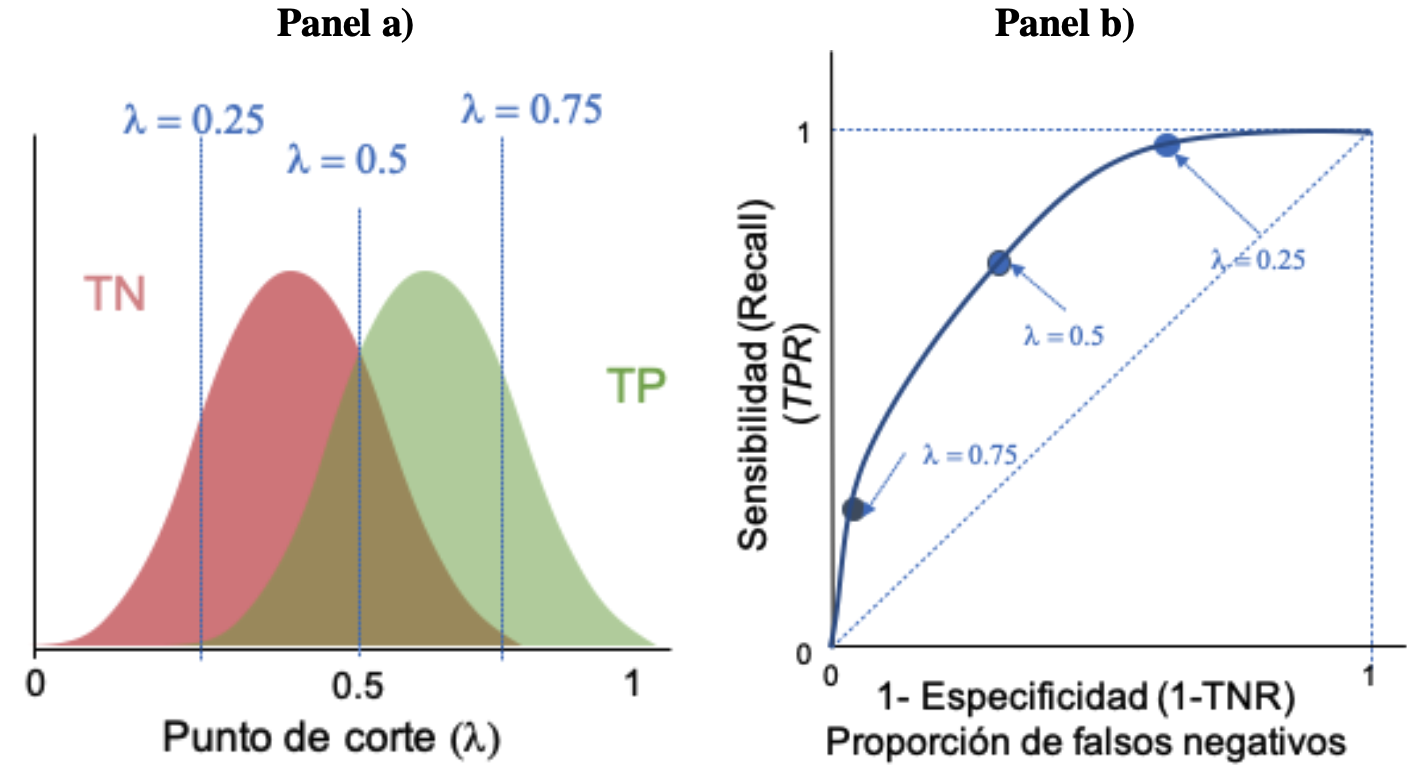
Es común que la primera aproximación sea definir a \(\lambda = 0.5\), pero esta selección es arbitraría. \(\lambda\) puede ser seleccionada por el científico de datos para ajustar la precisión del modelo. En la Figura 2.4 se presentan diferentes valores de corte (\(\lambda\)). Noten que los valores predichos como uno o cero para un individuo puede cambiar dependiendo del valor de corte seleccionado. Esto nos lleva a la necesidad de evaluar para un modelo, diferentes \(\lambda\), pues la aproximación se puede comportar de manera diferente para cada punto de corte para la probabilidad. En la siguiente sección se discuten las medidas de ajuste que emplearemos una vez se tengan los valores estimados para \(y_i\).

Figura 2.4: Ejemplo de diferentes valores de \(\lambda\)

Fuente: elaboración propia.

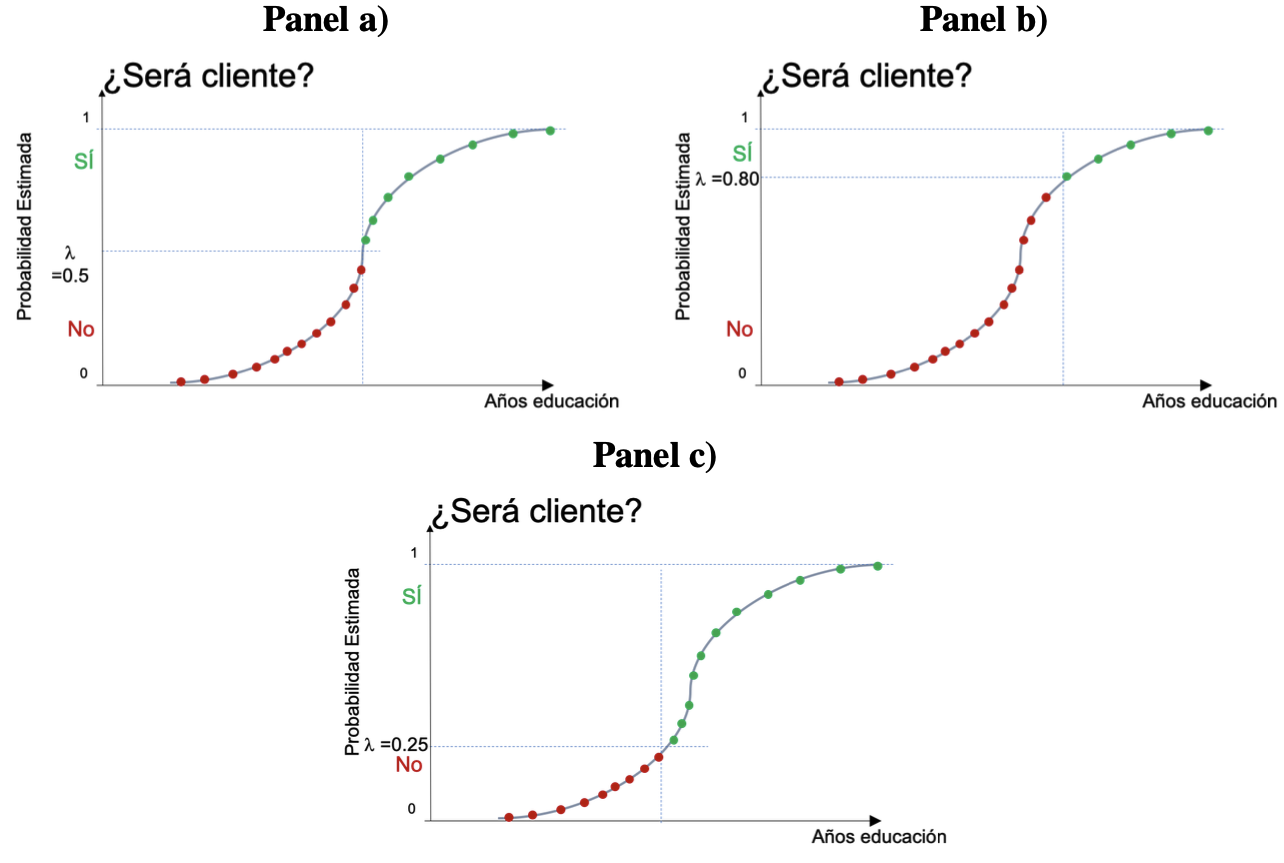
2.3.2 Medidas de ajuste del modelo basadas en la “exactitud” de la predicción

Una vez contamos con la clasificación construida por cada modelo para los individuos en unos \(\hat{y}_i = 1\) y ceros \(\hat{y}_i = 0\), podemos emplear diferentes métricas que intentan constatar que tan cerca está el modelo para predecir de manera exacta la clasificación del individuo. Para esto, se comparará la predicción con lo realmente observado en la muestra de evaluación.

2.3.2.1 Matriz de confusión

Para un determinado modelo¹⁷ podemos construir una matriz que en cada fila reporte el número de predicciones de cada clase, y en cada columna se registre los valores observados (reales) en la muestra de evaluación para cada clase. A este tipo de matriz se le conoce como matriz de confusión. En la Figura 2.5 se presenta un ejemplo de matriz de confusión para un caso en el que solo existen dos posibles clases.

Figura 2.5: Ejemplo matriz de confusión

Fuente: elaboración propia.

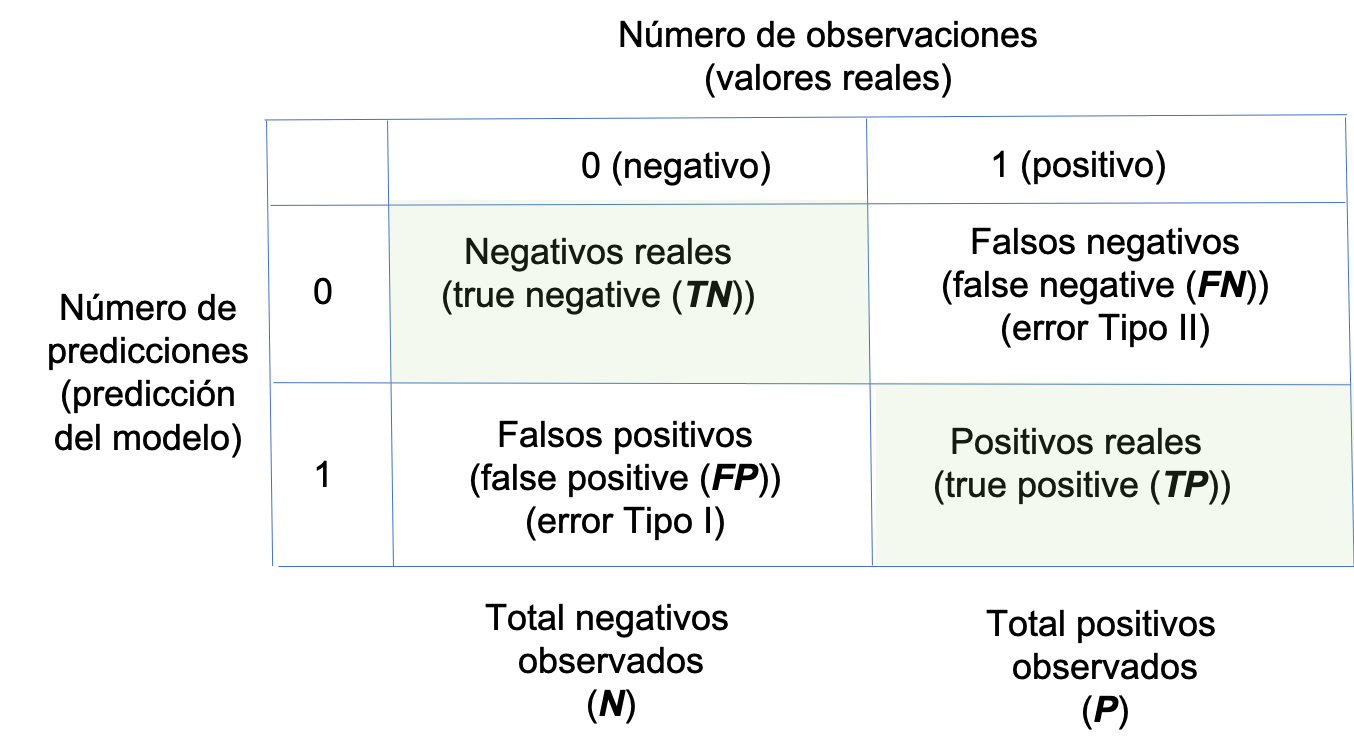
Ahora definamos las siguientes cantidades:

• \(N\): Total de negativos observados.
• \(P\): Total positivos observados.
• \(TN\): El número de negativos reales. Es decir, el número de predicciones negativas (0) que son iguales al valor real observado (true negative).
• \(TP\): El número de positivos reales (true positive).
• \(FN\): El número de falsos negativos (false negative). Es decir, el número de predicciones negativas (0) que no aciertan. Esto se conoce en estadística como el error tipo II.
• \(FP\): El número de falsos positivos (false positive). Esto se conoce en estadística como el error tipo I.

La matriz de confusión puede ser muy útil si nos concentramos en la diagonal principal (\(TN\) y \(TP\)). Pero en algunos casos puede ser muy difícil comparar dos matrices de confusión de modelos candidatos, en especial cuando empezamos a tener diferentes valores entre los modelos en las posiciones por fuera de la diagonal principal. En otras palabras, al comparar matrices de confusión tendremos que monitorear lo que ocurre en las cuatro celdas de la matriz. Sería más fácil contar con un solo número que sintetice lo que ocurre en las cuatro celdas de la matriz. Por eso se han desarrollado diferentes medidas que permiten comparar modelos de clasificación. Estas métricas se presentan a continuación.

2.3.2.2 Sensibilidad

La sensibilidad representa la capacidad del modelo de clasificación de detectar correctamente los valores verdaderos. La sensibilidad también es conocida como recall, tasa de acierto (hit rate) o tasa de verdaderos positivos (true positive rate \(TPR\)).

Consideremos un ejemplo en el que se quieren clasificar unos individuos dadas sus características en dos categorías: los clientes y los no clientes. En este caso la sensibilidad del modelo sería la capacidad del algoritmo de identificar correctamente los clientes.

La sensibilidad se define como: \[\begin{equation} TPR = \frac{TP}{P} \tag{2.1} \end{equation}\]

En otras palabras, la sensibilidad representa la fracción de verdaderos positivos. Es decir, la probabilidad (no condicionada) de que el modelo de clasificación identifique correctamente los unos.

2.3.2.3 Especificidad

Por otro lado, la especificidad (\(TNR\) por la sigla en inglés del término tasa de verdaderos negativos) se centra en la otra esquina de la matriz de confusión. Esta corresponde a la probabilidad de que un individuo al que se le observa un cero sea clasificado como un cero. Es decir, cuál es la proporción de no clientes que han sido correctamente clasificados por el modelo como no cliente. La especificidad se define como: \[\begin{equation} TNR = \frac{TN}{N} \tag{2.2} \end{equation}\]

La especificidad también se conoce como selectividad (selectivity).

2.3.2.4 Precisión

La precisión o valor positivo predicho (\(PPV\) por su sigla en inglés) corresponde a la proporción de verdaderos positivos de todos los positivos que predice el modelo. Es decir, \[\begin{equation} PPV = \frac{TP}{TP + FP} \tag{2.3} \end{equation}\]

En otras palabras, el \(PPV\) corresponde a la probabilidad de que un positivo predicho por el modelo sea un verdadero positivo. Para nuestro ejemplo de los clientes, el \(PPV\) corresponde a la probabilidad de que uno de los clientes que es predicho por el modelo sea efectivamente un cliente.

2.3.2.5 Valor negativo predictivo

El valor negativo predictivo (\(NPV\) por su sigla en inglés) corresponde a la proporción de verdaderos negativos de todos los negativos que predice el modelo. Es decir,

\[\begin{equation} NPV = \frac{TN}{TN + FN} \tag{2.4} \end{equation}\]

En nuestro ejemplo, el \(NPV\) es la probabilidad de que un no cliente predicho por el modelo sea realmente un no cliente.

2.3.2.6 Exactitud

La exactitud (\(ACC\)) (o conocido por su nombre en inglés accuracy)¹⁸ se utiliza también como una medida de qué tan bien se comporta un modelo de clasificación. Esta medida tiene en cuenta tanto elementos que se miden en la sensibilidad (recall) y en la especificidad. Se concentra en la proporción de aciertos tanto en negativos como en positivos. Es decir, en la diagonal principal de la matriz de confusión. La exactitud se mide como:

\[\begin{equation} ACC = \frac{TP + TN}{P+N} \tag{2.5} \end{equation}\]

En otras palabras, la exactitud es la proporción de resultados acertados (tanto verdaderos positivos (\(TP\)) como verdaderos negativos (\(TN\))) entre el número total de observaciones.

2.3.2.7 Puntaje \(F_1\)

Otra métrica de la bondad del modelo que emplea directamente la sensibilidad (recall) y la especificidad es el puntaje \(F_1\) (\(F_1\) score). Este indicador se calcula de la siguiente manera: \[\begin{equation} F_1 = 2 \cdot \frac{PPV \cdot TPR}{PPV + TPR} = \frac{2 \cdot TP}{2 \cdot TP + FP + FN} \tag{2.6} \end{equation}\]

Esta métrica corresponde a un promedio armónico (no aritmético) de la sensibilidad (recall) y la especificidad. La intuición detrás de este indicador es que al mismo tiempo que se está buscando un modelo que tenga una proporción alta de negativos correctamente predichos (alta precisión) se busca un porcentaje de todos los positivos cubiertos por el modelo (alta sensibilidad).

Recordemos que un indicador alto de precisión implica una mayor capacidad del modelo para clasificar los positivos correctamente. La combinación de esto con el recall da una idea de cuántos del total de positivos puede cubrir el modelo.

2.3.2.8 ROC y AUC para modelos con umbrales \(\lambda\)

La sensibilidad (\(TPR\)) y la especificidad (\(TNR\)) son inversamente proporcionales entre sí. Entonces, cuando aumentamos la sensibilidad, la especificidad disminuye y viceversa. Para modelos que proveen una probabilidad de positivos y no directamente una predicción de un positivo o negativo, se tiene que, cuando disminuimos el umbral \(\lambda\), obtenemos más valores positivos predichos (ver Figura 2.4 panel b), por lo que aumenta la sensibilidad y disminuye la especificidad. Del mismo modo, cuando aumentamos el umbral, obtenemos más valores negativos (ver Figura 2.4 panel c) y, por lo tanto, obtenemos una mayor especificidad y una menor sensibilidad. Las otras medidas discutidas anteriormente también se verán afectadas por el cambio de punto de corte, pero el impacto no es tan claro.

De la discusión anterior es claro que elegir el mejor modelo de clasificación implica encontrar un equilibrio entre predecir con precisión los positivos y los negativos. En otras palabras, un balance entre la sensibilidad (recall) y la especificidad. Así mismo, estas dos cantidades dependen del punto de corte.

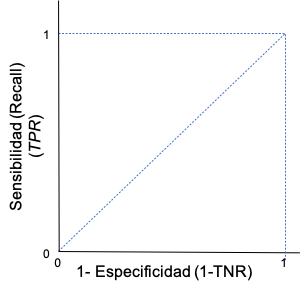
La curva de ROC (por la sigla del término en inglés Receiver Operating Characteristics) tiene como intención recoger este resultado. Para graficar la curva ROC emplearemos en el eje horizontal la proporción de falsos negativos, que corresponde a uno menos la proporción de verdaderos negativos predichos por el modelo. En otras palabras, uno menos la especificidad. En el eje vertical se presenta la sensibilidad (recall o tasa de positivos reales) (Ver Figura 2.6). La curva ROC muestra la combinación de proporción de falsos negativos y sensibilidad para cada determinado valor de corte.

Figura 2.6: Ejes de la Curva ROC

Fuente: elaboración propia.

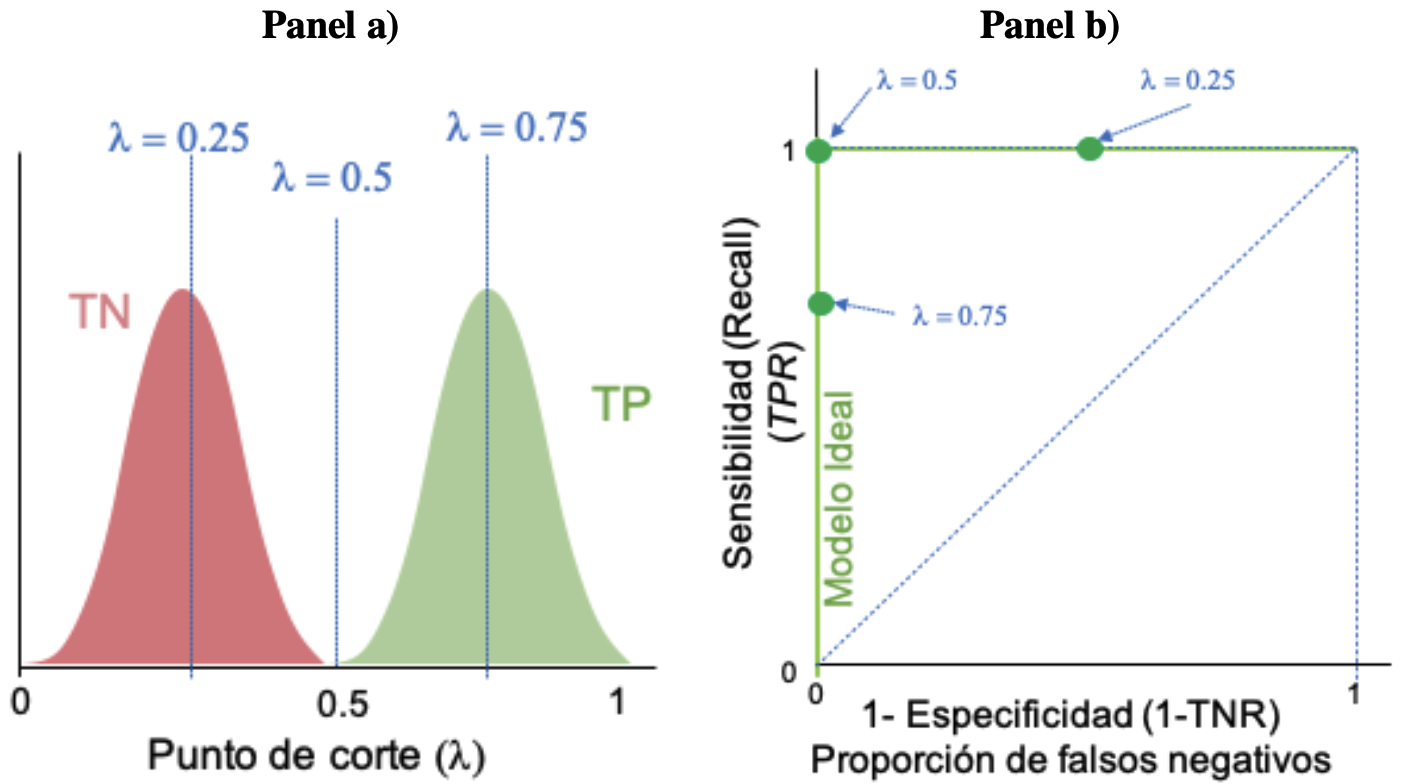
Ahora pensemos en la situación ideal. Una situación ideal es un modelo que permite generar una distribución de negativos (\(TN\)) y positivos (\(TP\)) que discrimine completamente los dos posibles estados como la que se describe en el panel a) de la Figura 2.7. Ahora supongamos un \(\lambda = 0.5\) (punto de corte). En este caso, la proporción de ceros falsos negativos es cero y la proporción de tasa de positivos reales (sensibilidad) es uno. Esta situación la representa un punto verde en la Figura 2.7 panel b) que se encuentra en el punto (0,1). Ahora, supongamos que aumentamos el punto de corte a \(\lambda = 0.75\). En este caso, la sensibilidad disminuirá; al mismo tiempo la proporción de ceros falsos negativos sigue siendo cero. Esto se representa con el punto verde sobre el eje vertical (ver Figura 2.7 panel b)). Ahora, supongamos que el punto de corte se disminuye a 0.25 (\(\lambda = 0.25\)). En ese caso la sensibilidad será 1 (proporción de verdaderas positivos predichos) y la proporción de falsos negativos aumentará. Esto se representa con un punto verde (ver Figura 2.7 panel b)). Así podemos seguir obteniendo diferentes puntos para diferentes puntos de corte. La unión de todos esos puntos es la curva ROC. En este caso el mejor de los escenarios implica una curva ROC que será una línea recta vertical de (0,0) hasta (0,1) y posteriormente vertical de (0,1) hasta (1,1).

Figura 2.7: Curva ROC del mejor modelo posible

Fuente: elaboración propia.

Ahora, supongamos un escenario base en el que se tiene un modelo de clasificación totalmente aleatorio, en el que no se sabe nada de los datos a clasificar. Ese modelo clasificaría de manera aleatoria a cada individuo mandándolos a cada una de las dos categorías con la misma distribución de probabilidad, como la que se describe en el panel a) de la Figura 2.8. En ese caso, un punto de corte de 0.5 implicará una proporción de falsos negativos igual a la sensibilidad (\(TPR\)). Esto se puede observar con un punto rojo en la Figura 2.8 panel b). Si aumentamos (disminuimos) el punto de corte la proporción de falsos negativos y la sensibilidad aumentarán (disminuirán). Si se realiza el mismo ejercicio para todos los valores de corte posibles, obtendremos una curva ROC que va desde el origen (0,0) hasta el punto (1,1) (ver Figura 2.8 panel b)). Esta línea se considera la línea de base para comparar los modelos de clasificación.

Figura 2.8: Curva ROC de un modelo aleatorio base

Fuente: elaboración propia.

En la práctica es poco común obtener curvas ROC como las descritas en las Figuras 2.7 y 2.8. Es más común observar curvas ROC como la descrita en la Figura 2.9.

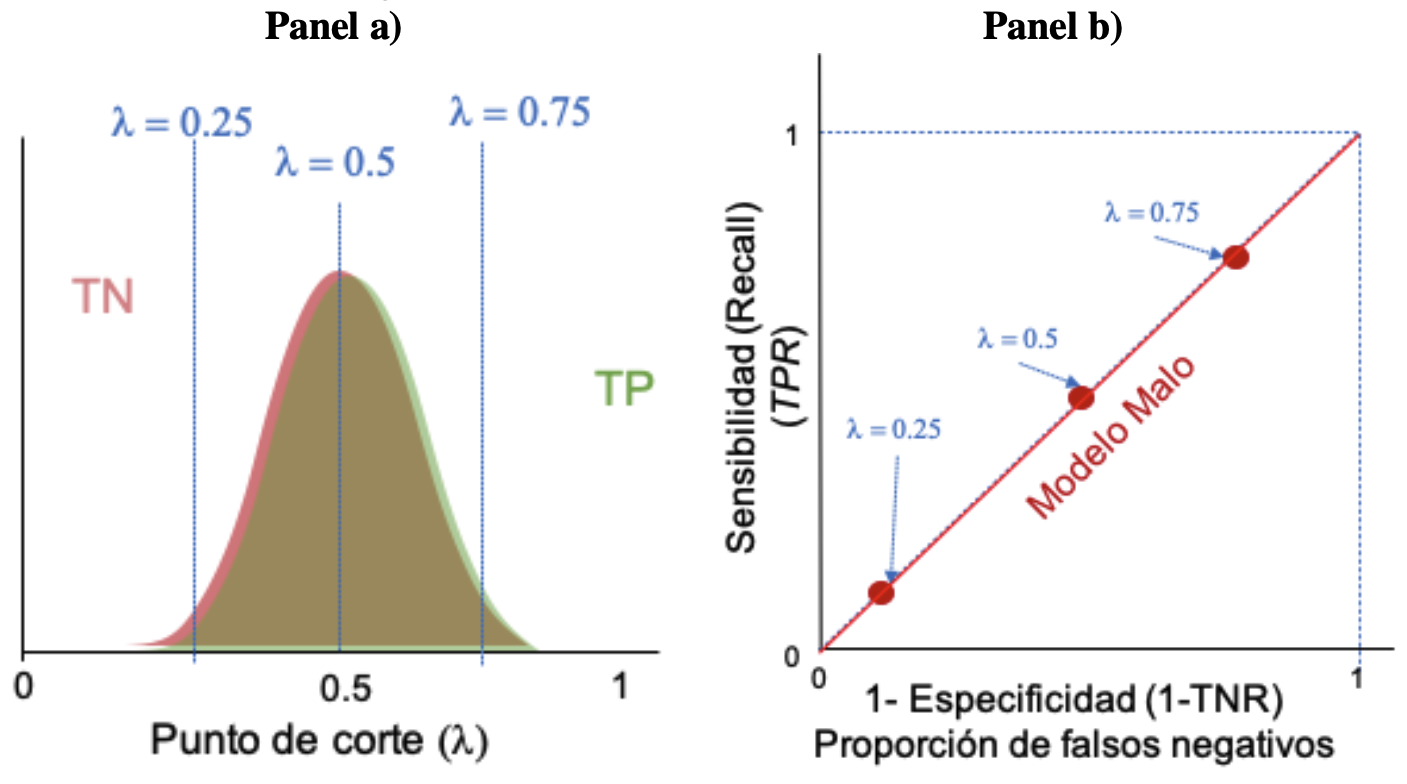
Figura 2.9: Curva ROC de un modelo típico de clasificación

Fuente: elaboración propia.

En algunos casos es complicado hacerle seguimiento a toda la curva para comparar varios modelos. Por ejemplo, las curvas ROC de dos modelos se pueden cruzar. Un indicador que resume la curva ROC es el Área Bajo la Curva ROC (AUC por la sigla en inglés Area under curve). Noten que en el caso ideal presentado en la Figura 2.7 panel b) el área bajo la curva es 1 (corresponde a un cuadrado con lados 1). En el caso del modelo de clasificación aleatorio que sirve como línea de base para un mal modelo (ver Figura 2.8 panel b), el AUC es \(\frac{1}{2}\) (el área del triángulo con base 1 y altura 1). Para la curva ROC presentada en la Figura 2.9 el AUC estará entre 0.5 y 1. En general el \(AUC\) entre más grande mejor será el modelo. Es relativamente común emplear la siguiente regla empírica para decidir sobre la bondad de ajuste del modelo:

• \(AUC = 0.5\): Es un mal clasificador, es como lanzar una moneda.
• \(0.5 \leq AUC < 0.6\): Modelo de clasificación es malo.
• \(0.6 \leq AUC < 0.75\): Modelo de clasificación es regular.
• \(0.75 \leq AUC < 0.9\): Modelo de clasificación es bueno.
• \(0.9 \leq AUC < 0.95\): Modelo de clasificación es muy bueno.
• \(0.97 \leq AUC < 1\): Modelo de clasificación es excelente.
• \(AUC = 1\): Modelo de clasificación es perfecto.

Noten que otra cosa importante que nos muestra la curva ROC para un modelo que genera una predicción de la probabilidad de ser un positivo de un individuo es el punto de corte (\(\lambda\)) que da la mejor combinación de sensibilidad y especificidad. El punto de la ROC que se aleje mas de la linea de base o que se acerque más al punto (0,1) será un buen candidato de punto de corte. Si bien existen varios criterios para encontrar el punto de corte óptimo, un método conocido es maximizar el Índice de Youden (Youden, 1950). Este índice se define como la suma de la selectividad y especificidad menos uno. Es decir:

\[\begin{equation} J = TPR + TNR - 1 \tag{2.7} \end{equation}\] Así, encontrar el punto de corte óptimo implicará calcular \(J\) para todos los posibles \(\lambda\) y seleccionar el \(\lambda\) donde el \(J\) se maximice.

2.4 Comentarios finales

La selección de la o las métricas adecuadas para la evaluación de los modelos dependerá de la pregunta de negocio y de lo que es deseable para cada organización.

Por otro lado, como se discutió anteriormente, las métricas se emplearán típicamente sobre muestras de evaluación y no de estimación o entrenamiento, para evitar el overfitting (sobreajuste). Así, como la métrica adecuada, se deberá escoger el esquema de validación cruzada que se empleará.

En los siguientes capítulos estudiaremos diferentes modelos de clasificación y emplearemos las técnicas de evaluación (métricas y estrategia de validación cruzada) para los modelos de clasificación estudiadas en este Capítulo.

Referencias

Alonso, J. C. (2024). Introducción al modelo clásico de regresión para científico de datos en r. Universidad Icesi. https://doi.org/XXXX

Youden, W. J. (1950). Index for rating diagnostic tests. Cancer, 3(1), 32–35.

---

12. En el mundo de la estadística se emplea la expresión “estimar un modelo” para la construcción de un modelo a partir de una muestra. Por otro lado, en el mundo de la inteligencia artificial se emplea la expresión “entrenar un modelo”.↩︎

13. Noten que esta técnica solo tiene sentido en datos de corte transversal, donde el orden de los datos no es importante.↩︎

14. Por muestreo aleatorio sin reposición.↩︎

15. Es importante resaltar que, en esta literatura cuando la variable dependiente toma el valor de uno se le conoce como un resultado positivo y en caso de tomar un cero se le denomina negativo. De aquí en adelante adoptaremos ese lenguaje por simplicidad.↩︎

16. El Valor de corte también es conocido como el umbral, Cutoff Value o treshold Value.↩︎

17. Los modelos o algoritmos pueden o no implicar un correspondiente valor de corte \(\lambda\).↩︎

18. Esta medida también es conocida en la literatura como valor predictivo positivo, exactitud Rand o índice Rand.↩︎