3 Modelo Logit

Objetivos del capítulo

Al finalizar la lectura de este documento, el estudiante estará en capacidad de:

Explicar en sus propias palabras cuál es la lógica detrás de un modelo Logit.
Estimar un modelo de regresión logística en R.
Emplear técnicas de selección automática de variables para construir un modelo Logit.

3.1 Generalidades

El modelo Logit es una generalización del modelo de regresión lineal múltiple¹⁹. El modelo de regresión lineal implica una variable dependiente que es continua (o que se supone continua)²⁰, en el caso de los modelos de clasificación, éstos tendrán una variable cualitativa como variable dependiente. Por ejemplo, si nos concentramos en los casos de clasificación en los que solo hay dos categorías, la variable dependiente será una variable dummy²¹ (dicotómica). Ejemplos de estas variables son: i) si un individuo pertenecerá o no a un grupo, ii) si un individuo será cliente o no, iii) si un individuo pagará o no.

Una posibilidad para estimar este tipo de modelos es emplear el modelo lineal y estimarlo por MCO. Esta aproximación de emplear el modelo lineal con una variable dependiente se conoce como el Modelo de Probabilidad Lineal (MPL). Lastimosamente esta aproximación de estimar por MCO el MPL tiene varios problemas, unos solucionables y otros no.

Los problemas más comunes de estimar modelos con variables dummy como dependientes por MCO son:

El error del modelo presenta problemas de heteroscedasticidad²². De hecho se sabe que en este caso: \(\sigma_i^2=E\left [ \mathbf{y_i} | \mathbf{x}_i \right ] \left( 1- E\left [ \mathbf{y_i} | \mathbf{x}_i \right ] \right)\), donde \(\mathbf{x}_i\) representa un vector fila de dimensiones (\(1 \times k\)) que recoge las características del individuo \(i\)²³.
El modelo estimado no garantiza que los valores estimados para la variable dependiente estén en el intervalo [0,1]. Esto implica, por ejemplo, varianzas negativas.

El primero de los problemas se puede solucionar empleando el método de Mínimos Cuadrados Ponderados (MCP).²⁴ El segundo problema no tiene una solución fácil y hace que este modelo no sea muy usado en la actualidad. Para entender en detalle este problema empleemos un ejemplo.

Supongamos que se desea explicar el hecho de que un individuo será cliente o no por medio de sólo una variable: los años de educación (\({X_{2,i}}\)), Es decir, se tiene que \({\mathbf{x}}_i = \left[ {1 , {X_{2i}}} \right]\), por tanto: \[\begin{equation} \begin{array}{c} {y_i} = {\beta ^T} {{\mathbf{x}}_{i}^{T}} + {\varepsilon_i} {y_i} = {\beta _1} + {\beta _2}{X_{2,i}} + {\varepsilon_i} \end{array} \tag{3.1} \end{equation}\]

Así, para estimar el modelo se tendrá que recoger datos de individuos que son clientes (\({y_i} = 1\)) y aquellos que no (\({y_i} = 0\)) y los respectivos años de educación de cada individuo. Al graficar estos datos tendremos algo parecido al panel a) de la Figura 3.1. Noten que sólo se tendrán observaciones de la variable dependiente con valores de 1 y 0. El método de MCO lo que intentará hacer es encontrar una línea recta que minimice la suma de la distancia cuadrada entre los puntos observados y la línea estimada. Así, se obtendrá una línea como la presentada en el panel b) de ese mismo gráfico. Noten que el modelo estimado (\({\hat y_i} = {\hat \beta _1} + {\hat \beta _2}{{X}_{2,i}}\)) no acota los valores estimados para la variable dependiente al intervalo [0,1] .

Figura 3.1: Modelo lineal con variable dummy como dependiente

Fuente: elaboración propia.

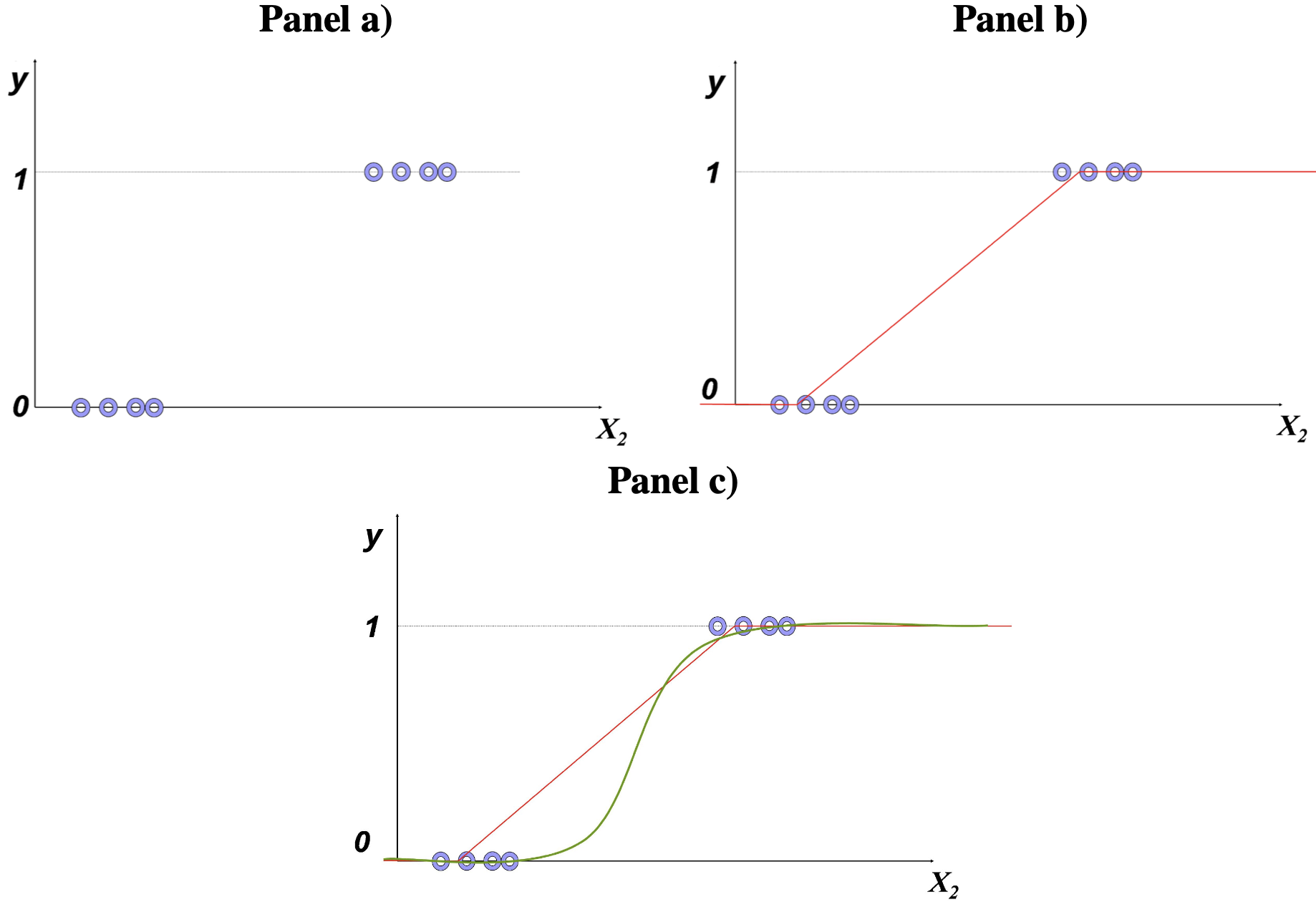
Además, este gráfico permite entender que un modelo lineal no podrá explicar de manera adecuada este tipo de modelos en los que la variable dependiente solo toma dos valores. De hecho, parece más adecuado emplear modelos no lineales para ajustar los datos, tal como se muestra en el panel c) de la Figura 3.1. Un modelo no lineal que se pueden emplear en estos casos es el modelo Logit²⁵.

Una manera de asegurar que los valores estimados del modelo se mantengan en el intervalo [0,1] es emplear una forma funcional acorde. Esto se garantiza empleando funciones de probabilidad acumulativa. Para entender cómo emplear estas funciones de probabilidad, empleemos el mismo ejemplo anterior, pero permitamos la posibilidad de más variables explicativas.

Es decir, suponga que se quiere explicar la variable \(y_i\), tal como se definió en nuestro ejemplo, empleando \(k-1\) variables explicatorias y una constante. Así, emplearemos el vector fila \({\mathbf{x}}_i\) de dimensiones (\(1 \times k\)), que recoge las características del individuo \(i\) para explicar la probabilidad de ser cliente.

Un individuo que está decidiendo ser cliente o no, tomará su decisión dependiendo de si el beneficio neto de ser cliente es positivo o no. Así, si el beneficio neto de ser cliente es positivo, el individuo participará y si éste es negativo, entonces el individuo no participará. Por ahora definamos el beneficio neto del individuo \(i\) como \(Z_i\). Noten que esta variable no es observable más adelante discutiremos esto. Así, tendremos que:

\[\begin{equation} y_i = \begin{cases} 1 & \text{ si } Z_i>0 \\ 0 & \text{ si } Z_i\leqslant 0 \end{cases} \tag{3.2} \end{equation}\]

Pero, ¿de qué depende ese beneficio neto? Supongamos que este es función de las características del individuo recolectadas en el vector \(\bf{x}_i\) . Es decir: \[\begin{equation*} \mathbf{Z}_i = \beta ^T \mathbf{x}_i^T + \varepsilon_i \end{equation*}\] Donde \(\varepsilon_i\) es un término aleatorio de error. Así, para unas características dadas para el individuo \(i\) tendremos que el valor esperado del beneficio neto será: \[\begin{equation*} E\left[ {{ Z_i} \left| {{{\mathbf{x}}_i} } \right.} \right] = {\bar Z_i} = \beta ^T {\bf x_i^T} \end{equation*}\]

Recapitulando, las características del individuo \(i\) (\({\mathbf{x}}_i\)) afectan el beneficio neto (\({Z_i}\)) y éste a su vez explica si el individuo es cliente o no; es decir, \(y_i\). Ahora bien, noten que la distribución del beneficio neto, dadas unas características del individuo \(i\) (\({\mathbf{x}}_i\)), dependerá de la distribución del término de error \(\varepsilon_i\).

Por conveniencia, podemos emplear el hecho que \({Z_i} = \beta ^T {{\mathbf{x}}_i^T} + \varepsilon_i > 0\) implica que \(\varepsilon_i > - \beta ^T {{\mathbf{x}}_i^T} = {-Z_i}\) para reescribir la ecuación (3.3) de la siguiente manera: \[\begin{equation} y_i = \begin{cases} 1 & \text{ si} -Z_i<0 \\ 0 & \text{ si} -Z_i \geqslant 0 \end{cases} \tag{3.3} \end{equation}\]

En el panel a) de la Figura 3.2 se puede observar un esquema de un individuo con una relativa baja probabilidad de ser cliente, dadas sus características; mientras que en el panel b) se puede observar un individuo con una probabilidad relativamente alta. Es importante anotar que la probabilidad está expresada por el área bajo la curva de la función de distribución y dependerá de la forma de ésta. Finalmente, cabe anotar que la función que determina el área bajo la curva a la izquierda de cualquier valor determinado de una función de distribución se conoce como la función de distribución acumulativa. Es decir, \[\begin{equation*} F\left( {Z_i } \right) = P\left( {Z_i \le c} \right) = \int\limits_{ - \infty }^c {f\left( t \right)dt} \end{equation*}\]

Figura 3.2: Distribución del beneficio neto (de la variable latente)

Fuente: elaboración propia.

En otras palabras se tendrá que: \[\begin{equation*} P\left[ Y_i = 0 | \mathbf{x}_i \right] = F\left( - Z_i \right) = F\left( - \beta ^T \mathbf{x}_i^T \right) \end{equation*}\] \[\begin{equation*} P\left[ Y_i = 1 | \mathbf{x}_i \right] = 1 - F\left( - Z_i \right) = 1 - F\left( - \beta ^T \mathbf{x}_i^T \right) \end{equation*}\]

Precisamente esta función de probabilidad acumulativa para distribuciones simétricas como la normal presenta una forma de “S” como la mostrada en el panel c) de la Figura 3.1.

Por otro lado, lastimosamente \(Z_i\) es una variable que los investigadores no pueden observar directamente, si bien se puede realizar una inferencia sobre esta al observar una variable relacionada, como lo es en este caso la variable dummy \(y_i\). A este tipo de variables se les denomina variable latente. Es decir, una variable latente es una variable no observable directamente, pero para la cual se puede inferir su valor a partir de una variable relacionada.

Retornando a nuestro problema de clasificación, lo que se desea es encontrar los coeficientes \(\beta\) que en últimas refleja el impacto de cada una de las variables explicativas sobre la probabilidad de que \(y_i\) sea uno. Es decir, dada una muestra de tamaño \(n\) y sus correspondientes características (\(\mathbf{x}_i\)) se desean encontrar los \(\beta's\) tal que \(P\left[ Y_i = 1 | \mathbf{x}_i \right] = 1 - F\left( - Z_i \right) = 1 - F\left( - \beta ^T \mathbf{x}_i^T \right)\) si el individuo es cliente y \(P\left[ Y_i = 0 | \mathbf{x}_i \right] = F\left( - Z_i \right) = F\left( - \beta ^T \mathbf{x}_i^T \right)\) si el individuo no es cliente.

A la probabilidad de que la i-ésima observación fuera igual a lo realmente observado se le denomina verosimilitud (en inglés likelihood). Así, la verosimilitud para un individuo sea cliente \(P\left[ y_i = 1 | \mathbf{x}_i \right]\) y para los que no son cliente es \(P\left[ y_i = 0 | \mathbf{x}_i \right]\). La función que recoge la verosimilitud (probabilidad) de que ocurra toda la muestra se conoce como la función de verosimilitud, es decir: \[\begin{equation*} L(\beta )= P(y) = \prod_{\forall y_i = 1}P\left ( y_i = 1 \right )\prod_{\forall y_i = 0}P\left ( y_i = 0 \right ) \end{equation*}\] O lo que es equivalente a: \[\begin{equation*} L(\beta )= \prod_{\forall y_i = 1}1 - F\left ( -Z_i \right )\prod_{\forall y_i = 0}F\left ( -Z_i \right ) \end{equation*}\]

Ahora bien, para encontrar los coeficientes \(\beta\) de este tipo de problemas ya no tiene mucho sentido emplear el método de mínimos cuadrados estudiado hasta el momento. De hecho tiene más sentido tratar de encontrar el vector de coeficientes (\(\beta\)) tal que la función de verosimilitud sea maximizada. A este método se le denomina Método de Máxima Verosimilitud; el cual implica encontrar los coeficientes tal que el chance de observar la muestra con que se cuenta sea el máximo posible, bajo el supuesto que la información sigue una distribución dada por \(F\left( \bullet \right)\).

En otras palabras, los estimadores de máxima verosimilitud corresponden a los coeficientes \(\hat \beta ^{MV}\) tal que: \[\begin{equation*} \mathop{Max}\limits_\beta L(\beta )= \mathop{Max}\limits_\beta \left [ P(y) \right ] = \mathop{Max}\limits_\beta \left [ \prod_{\forall y_i = 1}P\left ( y_i = 1 \right )\prod_{\forall y_i = 0}P\left ( y_i = 0 \right )\right ] \end{equation*}\] En otras palabras: \[\begin{equation} \mathop{Max}\limits_\beta L(\beta )= \ \mathop{Max}\limits_\beta \left [\prod_{\forall y_i = 1}1 - F\left ( -Z_i \right )\prod_{\forall y_i = 0}F\left ( -Z_i \right )\right ] \tag{3.4} \end{equation}\]

En general, es mucho más fácil maximizar el logaritmo de la función de máxima verosimilitud (conocida en inglés con el nombre de log likelihood function) que la expresión (3.4). Es decir, en la práctica el problema que se resuelve es: \[\begin{equation} \mathop {Max}\limits_\beta \ln \left( {L\left( \beta \right)} \right) = \mathop {Max}\limits_\beta \left[ {\ln \left( {P\left( Y \right)} \right)} \right] \tag{3.5} \end{equation}\]

Dado que la función logarítmica es una transformación monotónica, el vector \(\beta\) que resuelva el problema (3.4) también solucionará el problema (3.5). Es importante resaltar que es difícil encontrar, y en algunos casos no existe, una fórmula que siempre que se aplique dé solución al problema de Máxima Verosimilitud,²⁶ por tanto el proceso de maximización se resuelve de manera numérica empleando computadores.

Los estimadores de máxima verosimilitud son consistentes y siguen una distribución aproximadamente igual a la normal en muestras grandes. Así mismo, a medida que la muestra crece estos estimadores serán eficientes. Este resultado hace que la inferencia sobre los coeficientes, tanto individual como conjunta, sea igual que lo estudiado para los estimadores MCO.

3.2 Detalles del modelo Logit

En especial, para el modelo Logit se supone que la función acumulativa de distribución proviene de una distribución logística²⁷. En este caso tendremos que: \[\begin{equation*} F\left( {{Z_i}} \right) = \frac{{{e^{ - {Z_i}}}}}{{1 + {e^{ - {Z_i}}}}} = \Lambda \left( { - {Z_i}} \right) \end{equation*}\] Entonces los estimadores de Máxima Verosimilitud implicarán resolver el siguiente problema \[\begin{equation*} \mathop {Max}\limits_\beta \left( {\ln \left[ {\prod\limits_{\forall i\,tal\,que\,{y_i} = 1} {\left( {1 - \Lambda \left( { - {Z_i}} \right)} \right)} \prod\limits_{\forall i\,tal\,que\,{y_i} = 0} {\left( {\Lambda \left( { - {Z_i}} \right)} \right)} } \right]} \right) \end{equation*}\] Para el modelo Logit los coeficientes \(\beta\) no tienen interpretación por sí solos. En este caso tenemos que: \[\begin{equation*} E\left[ {{{y_i}}\left| {{{{\mathbf{x}}_i}}} \right.} \right] = 1 \bullet \left( {1 - \Lambda \left( { {\bf - {Z_i}}} \right)} \right) + 0 \bullet \Lambda \left( {{\bf - {Z_i}}} \right) = 1 - \Lambda \left( { {\bf - {Z_i}}} \right) \end{equation*}\] Y, por tanto, \[\begin{equation*} \frac{{\partial E\left[ {{{\bf{y}}_{\bf{i}}}\left| {{{\bf{x}}_{\bf{i}}}} \right.} \right]}}{{\partial {{\bf{X}}_{\bf{j}}}}} = - \frac{{\partial \Lambda \left( { - {{\bf{Z}}_{\bf{i}}}} \right)}}{{\partial {{\bf{X}}_{\bf{j}}}}}{\beta _j} = \Lambda \left( {{{\bf{Z}}_{\bf{i}}}} \right)\left[ {1 - \Lambda \left( {{{\bf{Z}}_{\bf{i}}}} \right)} \right]{\beta _j} \end{equation*}\]

Noten que para el modelo Logit se tiene que el efecto marginal de \(X_j\) no es el mismo para todos los individuos. Si la muestra es relativamente grande, puede ser muy complicado analizar el efecto marginal de cada una de las variables explicativas para cada uno de los elementos de la muestra. En ese caso una práctica común es calcular todos los efectos marginales para la muestra y calcular el promedio de este. Es decir: \[\begin{equation*} \frac{{\sum\limits_{i = 1}^n {\Lambda \left( {{Z_i}} \right)\left[ {1 - \Lambda \left( {{Z_i}} \right)} \right]{\beta _j}} }}{n} \end{equation*}\]

Como se mencionó anteriormente, los computadores pueden encontrar fácilmente por medio de métodos numéricos el vector de coeficientes \({\beta ^{MV}}\) que resuelve este problema y su correspondiente matriz de varianzas y covarianzas.

3.3 Aplicación del modelo Logit en R

Para realizar un ejemplo práctico emplearemos una base de datos provista por Moro et al. (2014)²⁸. Los datos están relacionados con varias campañas de marketing directo de una institución bancaria portuguesa. Las campañas de marketing se basaron en llamadas telefónicas. A menudo, se requería más de un contacto con el mismo cliente para determinar si el producto (bank term deposit) sería adquirido (yes) o no.

La base de datos contiene información de 41.188 clientes para 20 variables explicativas y una variable dependiente. Las variables relacionadas con los datos del cliente son:

age: edad (numérico)
job: tipo de trabajo (categórica: “admin.”, “blue-collar”, “entrepreneur”, “housemaid”, “management”, “retired”, “self-employed”, “services”, “student”, “technician”, “unemployed”, “unknown”)
marital: estado civil (categórica: “divorced”, “married”, “single”, “unknown”; nota: “divorced” significa divorciado o viudo)
education: educación (categórica: “basic.4y”, “basic.6y”, “basic.9y”, “high.school”, “illiterate”, “professional.course”, “university.degree”, “unknown”)
default: incumplimiento: ¿tiene crédito en incumplimiento? (categórica: “no”, “yes”, “unknown”)
housing: vivienda. ¿tiene préstamo de vivienda? (categórica: “no”, “yes”, “unknown”)
loan: préstamo. ¿tiene préstamo personal? (categórica: “no”, “yes”, “unknown”)

Variables relacionadas con el último contacto de la campaña actual:

contact: contacto. Tipo de comunicación de contacto (categórica: “cellular”, “telephone”)
month: meses. Último mes del año de contacto (categórica: “jan”, “feb”, “mar”, …, “nov”, “dec”)
day_of_week: Día de la semana. Último día de contacto de la semana (categórica: “mon”, “tue”, “wed”, “thu”, “fri”)
duration: duración. Duración del último contacto, en segundos (numérico). Nota importante: este atributo afecta en gran medida la variable dependiente (por ejemplo, si duration=0, entonces y = “no”). Sin embargo, la duración no se conoce antes de realizar una llamada. Además, después del final de la llamada, obviamente se conoce y. Por lo tanto, esta variable de entrada solo debe incluirse con fines de referencia y debe descartarse si la intención es tener un modelo predictivo realista.

Otras variables relacionadas con las campañas de mercadeo:

campaign: campaña. número de contactos realizados durante esta campaña y para este cliente (numérica, incluye el último contacto)
pdays: número de días que pasaron después que el cliente fue contactado por última vez desde una campaña anterior (numérica; 999 significa que el cliente no fue contactado previamente)
previous: número de contactos realizados antes de esta campaña y para este cliente (numérica)
poutcome: resultado de la campaña de marketing anterior (categórica: “failure”, “nonexistent”, “success”)

Variables asociadas al contexto:

emp.var.rate: tasa de variación del empleo - indicador trimestral (numérica)
cons.price.idx: índice de precios al consumidor - indicador mensual (numérica)
cons.conf.idx: índice de confianza del consumidor - indicador mensual (numérica)
euribor3m: tasa de interés euribor a 3 meses - indicador diario (numérica)
nr.employed: el número de empleados que tenía el banco (numérica)

La variable que se quiere explicar es:

y: ¿ha suscrito el cliente un depósito a plazo? (binario: “yes”, “no”)

La pregunta de negocio que queremos responder en este caso es: ¿se puede construir un modelo que pueda predecir si un cliente adquirirá o no el producto bancario?

Empecemos por cargar los datos que se encuentran en el archivo bank-additional-full.csv²⁹

#Cargar los datos
datos_originales <- read.csv("./datos/bank-additional-full.csv", sep = ";")

Recuerden que la variable duration no es útil para hacer la estimación (Ver descripción de las variables arriba). Entonces quitemos esta variable de nuestra muestra empleando la función subset() de la base de R.

# Eliminar la variable duration
datos <- subset(datos_originales, select=-duration)

Por otro lado, para la variable pdays³⁰ se tiene que el 96.3% de los individuos no fueron contactados. Por eso, descartaremos esa variable del análisis.

# Eliminar la variable duration
datos <- subset(datos, select=-pdays)

Finalmente, la variable nr.employed³¹ es una variable con poca variabilidad³² por eso la sacaremos de nuestro análisis.

# Eliminar la variable nr.employed
datos <- subset(datos, select=-nr.employed)

Ahora asegurémonos que las variables están bien definidas y las que no lo están, las cambiaremos. Adicionalmente, asegurémonos que en la variable dependiente tendremos los “yes” y “no” como positivos (unos) y negativos (ceros), respectivamente. Esto lo podemos hacer con la función relevel() del paquete base de R. Con esta función solo necesitamos un primer argumento con la variable a transformar y un segundo argumento (ref) que especifica el valor de la variable a transformar que se empleará como el nivel de referencia (igual a 1). Es decir, en este caso:

# Chequear la clase de las variables
library(dplyr)
glimpse(datos)

## Rows: 41,188
## Columns: 18
## $ age            <int> 56, 57, 37, 40, 56, 45, 59, 41, 24, 25, 41, 25, 29, 57,…
## $ job            <chr> "housemaid", "services", "services", "admin.", "service…
## $ marital        <chr> "married", "married", "married", "married", "married", …
## $ education      <chr> "basic.4y", "high.school", "high.school", "basic.6y", "…
## $ default        <chr> "no", "unknown", "no", "no", "no", "unknown", "no", "un…
## $ housing        <chr> "no", "no", "yes", "no", "no", "no", "no", "no", "yes",…
## $ loan           <chr> "no", "no", "no", "no", "yes", "no", "no", "no", "no", …
## $ contact        <chr> "telephone", "telephone", "telephone", "telephone", "te…
## $ month          <chr> "may", "may", "may", "may", "may", "may", "may", "may",…
## $ day_of_week    <chr> "mon", "mon", "mon", "mon", "mon", "mon", "mon", "mon",…
## $ campaign       <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
## $ previous       <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ poutcome       <chr> "nonexistent", "nonexistent", "nonexistent", "nonexiste…
## $ emp.var.rate   <dbl> 1.1, 1.1, 1.1, 1.1, 1.1, 1.1, 1.1, 1.1, 1.1, 1.1, 1.1, …
## $ cons.price.idx <dbl> 93.994, 93.994, 93.994, 93.994, 93.994, 93.994, 93.994,…
## $ cons.conf.idx  <dbl> -36.4, -36.4, -36.4, -36.4, -36.4, -36.4, -36.4, -36.4,…
## $ euribor3m      <dbl> 4.857, 4.857, 4.857, 4.857, 4.857, 4.857, 4.857, 4.857,…
## $ y              <chr> "no", "no", "no", "no", "no", "no", "no", "no", "no", "…

# Crear la variable dependiente como factor
datos$y <- relevel(as.factor(datos$y), ref = "no")

Antes de continuar, no es una buena práctica emplear “.” en el nombre de las variables. Miremos el nombre de las variables con el siguiente código:

names(datos)

##  [1] "age"            "job"            "marital"        "education"     
##  [5] "default"        "housing"        "loan"           "contact"       
##  [9] "month"          "day_of_week"    "campaign"       "previous"      
## [13] "poutcome"       "emp.var.rate"   "cons.price.idx" "cons.conf.idx" 
## [17] "euribor3m"      "y"

Cambiemos los “.” por “_” en el nombre de las variables empleando la función clean_names() del paquete janitor. (Firke, 2023)

library(janitor)
datos <- clean_names(datos)
names(datos)

##  [1] "age"            "job"            "marital"        "education"     
##  [5] "default"        "housing"        "loan"           "contact"       
##  [9] "month"          "day_of_week"    "campaign"       "previous"      
## [13] "poutcome"       "emp_var_rate"   "cons_price_idx" "cons_conf_idx" 
## [17] "euribor3m"      "y"

Ahora inspeccionemos la proporción de clientes que adquirieron el producto. Esto lo podemos hacer fácilmente en R (R Core Team, 2023) de la siguiente manera:

table(datos$y)

## 
##    no   yes 
## 36548  4640

table(datos$y)/nrow(datos)*100

## 
##       no      yes 
## 88.73458 11.26542

En este caso tenemos una muestra relativamente balanceada entre los no y los yes³³. Es importante anotar que si la muestra tiene muy pocos valores de una de las clases de la variable dependiente se puede producir un problema denominado el sesgo por datos desbalanceados. Dicho sesgo se puede solucionar utilizando técnicas de muestreo para equilibrar las clases. Algunas de estas técnicas incluyen el submuestreo de la clase mayoritaria o el sobremuestreo de la clase minoritaria. Otra opción es utilizar algoritmos de clasificación que sean menos sensibles al desbalance de clases, como el Random Forest (Ver Capítulo 8) o el Support Vector Machine (Ver Capítulo 9). Además, es importante evaluar el desempeño del modelo utilizando métricas adecuadas para datos desbalanceados, como la precisión, la sensibilidad y la especificidad. Pero siempre será necesario analizar cómo las métricas se pueden ver afectadas por el desbalanceo de la muestra. Cómo solucionar ese problema se discutirá en parte en el Capítulo 10.

Como se anotó en el Capítulo 1, es importante tener una estrategia de validación cruzada. Por simplicidad, empleemos el método de retención (holdout method). Procedamos a crear la muestra de estimación y la de evaluación siguiendo la costumbre de retener el 20% para la evaluación del modelo. Dado que se trata de una muestra de corte trasversal no existe ningún problema en generar este tipo de muestra, primero seleccionemos de manera aleatoria qué observaciones harán parte de cada una de estas muestras.

Hay que recordar que, debido a la naturaleza aleatoria de la muestra que vamos a generar, es importante emplear una semilla para la generación de números aleatorios³⁴ para garantizar que la muestra generada sea la misma para ti y para nosotros. En R podemos emplear la función set.seed() de la base de R para fijar la semilla. Creemos una muestra aleatoria con los índices (número de observación) de las observaciones que harán parte de nuestra muestra de estimación (80% de las observaciones de la muestra original). Esto lo podemos hacer de la siguiente manera:

set.seed(123)
# filas que harán parte de la muestra de estimación
est_index <- sample(1:nrow(datos), 0.8 * nrow(datos))
# filas que harán parte de la muestra de evaluación
eval_index <- setdiff(1:nrow(datos), est_index)

Ahora extraigamos las correspondientes observaciones para armar las dos muestras.

# muestra de estimación
datos_est <- datos[est_index,]

# muestra de evaluación
datos_eval <- datos[eval_index,]

Antes de continuar, constatemos que las dos muestras siguen estando balanceadas.

table(datos_est$y)

## 
##    no   yes 
## 29185  3765

table(datos_est$y)/nrow(datos_est)*100

## 
##      no     yes 
## 88.5736 11.4264

table(datos_eval$y)

## 
##   no  yes 
## 7363  875

table(datos_eval$y)/nrow(datos_eval)*100

## 
##       no      yes 
## 89.37849 10.62151

3.3.1 Estimación del modelo

En este caso \(\mathbf{x}_i\) corresponde a las 19 variables explicativas que tenemos³⁵ y el objetivo nuestro es estimar un modelo Logit por medio del método de máxima verosimilitud. De esta manera, el modelo Logit para explicar la probabilidad de adquirir el producto está dado por: \[\begin{equation*} P\left( y_i = 1 | \mathbf{x}_i^T \right) = \Lambda \left( \beta ^T\mathbf{x}_i^T \right) \end{equation*}\] donde \(\Lambda \left( Z \right) = \frac{{{e^Z}}}{{1 + {e^Z}}}\); es decir, la función de densidad logística. Como se discutió, el vector de coeficientes \(\beta\) puede ser estimado por medio del método de máxima verosimilitud, que equivale a resolver el siguiente problema: \[\begin{equation*} \mathop {Max}\limits_{\hat \beta } P\left( Y| X \right) = \mathop {Max}\limits_{\hat \beta } \left[ {\prod\limits_{i = 1}^n {\Lambda \left( \beta ^T\mathbf{x}_i^{\mathbf{T}} \right)} } \right] \end{equation*}\]

Este problema es equivalente a resolver lo siguiente: \[\begin{equation*} \mathop {Max}\limits_{\hat \beta } l\left( {Y\left| X \right.} \right) = \mathop {Max}\limits_{\hat \beta } \left[ {\prod\limits_{i = 1}^n {\ln \left[ {\Lambda \left( {{\beta ^T}{\bf{x}}_{\bf{i}}^{\bf{T}}} \right)} \right]} } \right] \end{equation*}\] donde \(\ln \left[ \bullet \right]\) corresponde al logaritmo natural y \(l\left( {Y\left| X \right.} \right)\) es conocido como el logaritmo de la función de verosimilitud.

En R podemos emplear la función glm() del core de R. Esta función estima modelos generalizados lineales que son una generalización de los modelos de regresión lineal. Esta función tiene argumentos muy similares a lm(). Debemos expresar el modelo a estimar, los datos y en este caso tenemos el argumento family que permite determinar el tipo de modelo a estimar. Para estimar un modelo Logit necesitamos que family = “binomial”. Estimemos un modelo con todas las variables como explicativas.

modelo <- glm(y~., data = datos_est, family = "binomial")
summary(modelo)

## 
## Call:
## glm(formula = y ~ ., family = "binomial", data = datos_est)
## 
## Coefficients: (1 not defined because of singularities)
##                                Estimate Std. Error z value Pr(>|z|)    
## (Intercept)                  -1.427e+02  1.015e+01 -14.060  < 2e-16 ***
## age                           1.236e-03  2.355e-03   0.525 0.599736    
## jobblue-collar               -1.469e-01  7.651e-02  -1.920 0.054895 .  
## jobentrepreneur              -9.625e-03  1.169e-01  -0.082 0.934374    
## jobhousemaid                 -9.353e-02  1.447e-01  -0.646 0.518061    
## jobmanagement                -7.601e-03  8.295e-02  -0.092 0.926994    
## jobretired                    2.676e-01  1.046e-01   2.559 0.010505 *  
## jobself-employed             -4.614e-02  1.132e-01  -0.408 0.683527    
## jobservices                  -1.181e-01  8.395e-02  -1.407 0.159574    
## jobstudent                    2.744e-01  1.107e-01   2.478 0.013219 *  
## jobtechnician                 1.278e-02  6.935e-02   0.184 0.853773    
## jobunemployed                 5.209e-02  1.223e-01   0.426 0.670080    
## jobunknown                   -1.691e-01  2.309e-01  -0.732 0.464034    
## maritalmarried               -4.538e-02  6.522e-02  -0.696 0.486571    
## maritalsingle                 1.334e-02  7.466e-02   0.179 0.858153    
## maritalunknown                4.175e-01  3.942e-01   1.059 0.289585    
## educationbasic.6y             1.024e-01  1.162e-01   0.881 0.378173    
## educationbasic.9y            -1.063e-02  9.189e-02  -0.116 0.907896    
## educationhigh.school          2.885e-02  8.919e-02   0.323 0.746322    
## educationilliterate           1.105e+00  7.391e-01   1.495 0.134969    
## educationprofessional.course  3.504e-02  9.825e-02   0.357 0.721355    
## educationuniversity.degree    1.059e-01  8.929e-02   1.186 0.235484    
## educationunknown              1.364e-01  1.159e-01   1.177 0.239310    
## defaultunknown               -2.658e-01  6.388e-02  -4.161 3.17e-05 ***
## defaultyes                   -8.621e+00  1.136e+02  -0.076 0.939485    
## housingunknown               -3.343e-02  1.310e-01  -0.255 0.798505    
## housingyes                   -2.255e-02  4.003e-02  -0.563 0.573201    
## loanunknown                          NA         NA      NA       NA    
## loanyes                      -1.075e-02  5.504e-02  -0.195 0.845115    
## contacttelephone             -6.396e-01  7.083e-02  -9.031  < 2e-16 ***
## monthaug                      2.435e-01  1.072e-01   2.271 0.023148 *  
## monthdec                      1.849e-01  1.990e-01   0.929 0.352930    
## monthjul                      8.224e-02  9.162e-02   0.898 0.369410    
## monthjun                     -4.841e-01  1.023e-01  -4.733 2.21e-06 ***
## monthmar                      1.313e+00  1.194e-01  10.997  < 2e-16 ***
## monthmay                     -5.060e-01  7.361e-02  -6.873 6.29e-12 ***
## monthnov                     -5.920e-01  1.031e-01  -5.739 9.51e-09 ***
## monthoct                     -2.593e-01  1.239e-01  -2.092 0.036400 *  
## monthsep                     -9.049e-02  1.315e-01  -0.688 0.491233    
## day_of_weekmon               -2.205e-01  6.419e-02  -3.435 0.000593 ***
## day_of_weekthu                8.446e-02  6.155e-02   1.372 0.169968    
## day_of_weektue                1.253e-02  6.386e-02   0.196 0.844453    
## day_of_weekwed                1.646e-01  6.294e-02   2.614 0.008938 ** 
## campaign                     -5.211e-02  1.046e-02  -4.981 6.33e-07 ***
## previous                      1.159e-01  5.936e-02   1.953 0.050811 .  
## poutcomenonexistent           5.805e-01  9.601e-02   6.046 1.48e-09 ***
## poutcomesuccess               1.734e+00  8.806e-02  19.694  < 2e-16 ***
## emp_var_rate                 -1.230e+00  1.110e-01 -11.085  < 2e-16 ***
## cons_price_idx                1.493e+00  1.055e-01  14.154  < 2e-16 ***
## cons_conf_idx                 1.806e-02  5.547e-03   3.256 0.001128 ** 
## euribor3m                     3.722e-01  8.406e-02   4.428 9.52e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 23417  on 32949  degrees of freedom
## Residual deviance: 18396  on 32900  degrees of freedom
## AIC: 18496
## 
## Number of Fisher Scoring iterations: 10

Noten que hay unas variables no significativas. De hecho tenemos 17 posibles variables explicativas, esto implica (sin interacciones) \(1.31072\times 10^{5}\) posibles modelos. Empleemos una estrategia inteligente para encontrar un modelo candidato para ser el mejor modelo³⁶.

3.3.2 Selección automática de variables explicativas por medio de regresión paso a paso (Stepwise)

Ya conocemos la forma en que, el algoritmo Stepwise (en sus versiones adelante, atrás o ambos) puede ayudarnos a encontrar el mejor modelo en un ambiente de regresión múltiple (Ver Sección 3.5.4). Podemos aplicar el mismo algoritmo para el caso del modelo Logit. Para esto, podemos emplear la función step() del core de R. Esta función emplea el \(AIC\) o \(BIC\) para encontrar el mejor modelo de un objeto de la clase glm.

La función step() típicamente incluye los siguientes argumentos: step(object, scope, scale = 0, direction = c(“both”, “backward”, “forward”), trace = 1, keep = NULL, steps = 1000, k = 2)

donde:

object: un objeto de clase lm o gml que se empleará como el modelo inicial en el proceso de búsqueda.
scope: define el rango de modelos que serán examinados en la búsqueda. Debe ser una fórmula o una lista que contenga componentes superiores e inferiores.
direction: el tipo de búsqueda. Las opciones son “both”, “backward” o “forward”. El valor por defecto es direction = “both”. Si falta el argumento scope, la dirección predeterminada será “backward”.
steps: El número máximo de pasos a considerar en el algoritmo de búsqueda. El valor predeterminado es 1000.
k: Si k = log(n) se emplea el \(BIC\) como criterio de selección. El valor por defecto es k = 2 que corresponde al \(AIC\).

Empleemos esta función para encontrar el mejor modelo con el algoritmo forward.

# modelo sin variables explicativas
min_model <- glm(y~ 1, data = datos_est, family = "binomial")

# modelo con todas las potenciales variables
max_model <- glm(y~., data = datos_est, family = "binomial")

# usando forward stepwise para encontrar el mejor modelo
model_forward <- step(min_model, scope = list(lower = min_model, upper = max_model), 
                      direction = "forward")

El mejor modelo seleccionado es:

model_forward$formula

## y ~ euribor3m + month + poutcome + cons_price_idx + emp_var_rate + 
##     contact + day_of_week + campaign + job + default + cons_conf_idx + 
##     previous

formula_forward <- model_forward$formula
model_forward_sel <- glm(formula_forward, 
                         data = datos_est, 
                         family = "binomial")
summary(model_forward_sel)

## 
## Call:
## glm(formula = formula_forward, family = "binomial", data = datos_est)
## 
## Coefficients:
##                       Estimate Std. Error z value Pr(>|z|)    
## (Intercept)         -1.431e+02  1.014e+01 -14.107  < 2e-16 ***
## euribor3m            3.725e-01  8.404e-02   4.432 9.33e-06 ***
## monthaug             2.506e-01  1.070e-01   2.342 0.019157 *  
## monthdec             1.773e-01  1.986e-01   0.893 0.372063    
## monthjul             8.407e-02  9.138e-02   0.920 0.357590    
## monthjun            -4.845e-01  1.020e-01  -4.752 2.02e-06 ***
## monthmar             1.323e+00  1.192e-01  11.102  < 2e-16 ***
## monthmay            -5.115e-01  7.334e-02  -6.974 3.09e-12 ***
## monthnov            -5.933e-01  1.030e-01  -5.758 8.53e-09 ***
## monthoct            -2.657e-01  1.237e-01  -2.147 0.031807 *  
## monthsep            -9.273e-02  1.313e-01  -0.706 0.480107    
## poutcomenonexistent  5.840e-01  9.593e-02   6.088 1.15e-09 ***
## poutcomesuccess      1.736e+00  8.800e-02  19.729  < 2e-16 ***
## cons_price_idx       1.498e+00  1.054e-01  14.217  < 2e-16 ***
## emp_var_rate        -1.234e+00  1.109e-01 -11.122  < 2e-16 ***
## contacttelephone    -6.418e-01  7.081e-02  -9.063  < 2e-16 ***
## day_of_weekmon      -2.218e-01  6.413e-02  -3.459 0.000542 ***
## day_of_weekthu       8.578e-02  6.148e-02   1.395 0.162913    
## day_of_weektue       1.103e-02  6.378e-02   0.173 0.862648    
## day_of_weekwed       1.638e-01  6.289e-02   2.604 0.009221 ** 
## campaign            -5.162e-02  1.044e-02  -4.944 7.67e-07 ***
## jobblue-collar      -2.014e-01  6.288e-02  -3.203 0.001362 ** 
## jobentrepreneur     -2.064e-02  1.152e-01  -0.179 0.857848    
## jobhousemaid        -1.293e-01  1.380e-01  -0.937 0.348765    
## jobmanagement        1.238e-03  8.121e-02   0.015 0.987836    
## jobretired           2.513e-01  8.299e-02   3.028 0.002461 ** 
## jobself-employed    -4.327e-02  1.122e-01  -0.386 0.699776    
## jobservices         -1.561e-01  7.965e-02  -1.959 0.050062 .  
## jobstudent           2.669e-01  1.012e-01   2.637 0.008358 ** 
## jobtechnician       -7.333e-03  6.162e-02  -0.119 0.905269    
## jobunemployed        2.217e-02  1.207e-01   0.184 0.854298    
## jobunknown          -1.541e-01  2.276e-01  -0.677 0.498152    
## defaultunknown      -2.691e-01  6.297e-02  -4.274 1.92e-05 ***
## defaultyes          -8.655e+00  1.136e+02  -0.076 0.939252    
## cons_conf_idx        1.850e-02  5.529e-03   3.345 0.000822 ***
## previous             1.171e-01  5.929e-02   1.975 0.048278 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 23417  on 32949  degrees of freedom
## Residual deviance: 18406  on 32914  degrees of freedom
## AIC: 18478
## 
## Number of Fisher Scoring iterations: 10

Noten que las variables no significativas son parte de las variables dummy creadas en el proceso. Por ahora dejemos el modelo de esta manera.

Hagamos lo mismo para el algoritmo backward.

model_backward <- step(max_model, scope = list(lower = min_model, 
                                               upper = max_model), 
                                               direction = "backward")

El mejor modelo seleccionado es:

# inspeccionar la fórmula
model_backward$formula

## y ~ job + default + contact + month + day_of_week + campaign + 
##     previous + poutcome + emp_var_rate + cons_price_idx + cons_conf_idx + 
##     euribor3m

Noten que este modelo no es diferente al anterior.

Finalmente, empleemos el algoritmo both.

model_both <- step(min_model, scope = list(lower = min_model, 
                                           upper = max_model), 
                                           direction = "both")

El mejor modelo seleccionado es:

# inspeccionar la fórmula
model_both$formula

## y ~ euribor3m + month + poutcome + cons_price_idx + emp_var_rate + 
##     contact + day_of_week + campaign + job + default + cons_conf_idx + 
##     previous

Este modelo es igual al obtenido por los dos algoritmos anteriores. Ahora regresemos al modelo seleccionado:

summary(model_forward_sel)

## 
## Call:
## glm(formula = formula_forward, family = "binomial", data = datos_est)
## 
## Coefficients:
##                       Estimate Std. Error z value Pr(>|z|)    
## (Intercept)         -1.431e+02  1.014e+01 -14.107  < 2e-16 ***
## euribor3m            3.725e-01  8.404e-02   4.432 9.33e-06 ***
## monthaug             2.506e-01  1.070e-01   2.342 0.019157 *  
## monthdec             1.773e-01  1.986e-01   0.893 0.372063    
## monthjul             8.407e-02  9.138e-02   0.920 0.357590    
## monthjun            -4.845e-01  1.020e-01  -4.752 2.02e-06 ***
## monthmar             1.323e+00  1.192e-01  11.102  < 2e-16 ***
## monthmay            -5.115e-01  7.334e-02  -6.974 3.09e-12 ***
## monthnov            -5.933e-01  1.030e-01  -5.758 8.53e-09 ***
## monthoct            -2.657e-01  1.237e-01  -2.147 0.031807 *  
## monthsep            -9.273e-02  1.313e-01  -0.706 0.480107    
## poutcomenonexistent  5.840e-01  9.593e-02   6.088 1.15e-09 ***
## poutcomesuccess      1.736e+00  8.800e-02  19.729  < 2e-16 ***
## cons_price_idx       1.498e+00  1.054e-01  14.217  < 2e-16 ***
## emp_var_rate        -1.234e+00  1.109e-01 -11.122  < 2e-16 ***
## contacttelephone    -6.418e-01  7.081e-02  -9.063  < 2e-16 ***
## day_of_weekmon      -2.218e-01  6.413e-02  -3.459 0.000542 ***
## day_of_weekthu       8.578e-02  6.148e-02   1.395 0.162913    
## day_of_weektue       1.103e-02  6.378e-02   0.173 0.862648    
## day_of_weekwed       1.638e-01  6.289e-02   2.604 0.009221 ** 
## campaign            -5.162e-02  1.044e-02  -4.944 7.67e-07 ***
## jobblue-collar      -2.014e-01  6.288e-02  -3.203 0.001362 ** 
## jobentrepreneur     -2.064e-02  1.152e-01  -0.179 0.857848    
## jobhousemaid        -1.293e-01  1.380e-01  -0.937 0.348765    
## jobmanagement        1.238e-03  8.121e-02   0.015 0.987836    
## jobretired           2.513e-01  8.299e-02   3.028 0.002461 ** 
## jobself-employed    -4.327e-02  1.122e-01  -0.386 0.699776    
## jobservices         -1.561e-01  7.965e-02  -1.959 0.050062 .  
## jobstudent           2.669e-01  1.012e-01   2.637 0.008358 ** 
## jobtechnician       -7.333e-03  6.162e-02  -0.119 0.905269    
## jobunemployed        2.217e-02  1.207e-01   0.184 0.854298    
## jobunknown          -1.541e-01  2.276e-01  -0.677 0.498152    
## defaultunknown      -2.691e-01  6.297e-02  -4.274 1.92e-05 ***
## defaultyes          -8.655e+00  1.136e+02  -0.076 0.939252    
## cons_conf_idx        1.850e-02  5.529e-03   3.345 0.000822 ***
## previous             1.171e-01  5.929e-02   1.975 0.048278 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 23417  on 32949  degrees of freedom
## Residual deviance: 18406  on 32914  degrees of freedom
## AIC: 18478
## 
## Number of Fisher Scoring iterations: 10

Ahora intentemos crear variables dummy para los factores y evitar que algunas de las categorías no sean significativas. Podemos emplear la función dummy_cols() del paquete fastDummies (Kaplan, 2023). En el Capítulo 5 de Alonso (2024) se puede encontrar una descripción detallada de cómo funciona esta función.

library(fastDummies)
# Crear Dummies de la variable job
      dummies_job <- dummy_cols(datos$job, remove_first_dummy = TRUE, 
                                 remove_selected_columns = TRUE, omit_colname_prefix = TRUE) 
      # limpiar los nombres de las variables
      dummies_job <- clean_names(dummies_job)
      # simplificar los nombres
      names(dummies_job) <- c("j_blue_collar", "j_entrepreneur",  "j_housemaid", 
                              "j_management", "j_retired", "j_self_employed",
                              "j_services",  "j_student", "j_technician",  
                              "j_unemployed",  "j_unknown")
      

# Crear Dummies de la variable marital
      dummies_marital <- dummy_cols(datos$marital, remove_first_dummy = TRUE, 
                                 remove_selected_columns = TRUE) 
      
      # limpiar los nombres de las variables
      dummies_marital <- clean_names(dummies_marital)
      
      # simplificar los nombres
      names(dummies_marital) <- c("m_married", "m_single",  "m_unknown")

# Crear Dummies de la variable education
      dummies_education <- dummy_cols(datos$education, remove_first_dummy = TRUE, 
                                 remove_selected_columns = TRUE) 
      
      # limpiar los nombres de las variables
      dummies_education <- clean_names(dummies_education)
      
      # simplificar los nombres
      names(dummies_education) <- c("e_basic_6y", "e_basic_9y", "e_high_school",
                                    "e_illiterate" , "e_professional_course", 
                                    "e_university_degree", "e_unknown")

      
# Crear Dummies de la variable default
      dummies_default <- dummy_cols(datos$default, remove_first_dummy = TRUE, 
                                 remove_selected_columns = TRUE) 
      
      # limpiar los nombres de las variables
      dummies_default <- clean_names(dummies_default)    
      
      # simplificar los nombres
      names(dummies_default) <- c("def_unknown", "def_yes")     
      
# Crear Dummies de la variable housing
      dummies_housing <- dummy_cols(datos$housing, remove_first_dummy = TRUE, 
                                 remove_selected_columns = TRUE) 
      
      # limpiar los nombres de las variables
      dummies_housing <- clean_names(dummies_housing) 
      
      # simplificar los nombres
      names(dummies_housing) <- c("h_unknown", "h_yes")     
       
# Crear Dummies de la variable loan
      dummies_loan <- dummy_cols(datos$loan, remove_first_dummy = TRUE, 
                                 remove_selected_columns = TRUE) 
      
      # limpiar los nombres de las variables
      dummies_loan <- clean_names(dummies_loan)     
      
      # simplificar los nombres
      names(dummies_loan) <- c("l_unknown", "l_yes")     
 
      
# Crear Dummies de la variable contact
      dummies_contact <- dummy_cols(datos$contact, remove_first_dummy = TRUE, 
                                 remove_selected_columns = TRUE) 
      
      # limpiar los nombres de las variables
      dummies_contact <- clean_names(dummies_contact)    
      
      # simplificar los nombres
      names(dummies_contact) <- c("c_telephone")     
 
      
# Crear Dummies de la variable months
      dummies_month <- dummy_cols(datos$month, remove_first_dummy = TRUE, 
                                 remove_selected_columns = TRUE)
      # limpiar los nombres de las variables
      dummies_month <- clean_names(dummies_month)
            
      # simplificar los nombres
      names(dummies_month) <- c("mon_aug", "mon_dec", "mon_jul", "mon_jun", 
                                "mon_mar", "mon_may", "mon_nov", "mon_oct", 
                                "mon_sep") 

# Crear Dummies de la variable dummies_dayWeek
    dummies_dayWeek <- dummy_cols(datos$day_of_week, remove_first_dummy = TRUE, 
                               remove_selected_columns = TRUE)
    # limpiar los nombres de las variables
    dummies_dayWeek <- clean_names(dummies_dayWeek)
          
    # simplificar los nombres
    names(dummies_dayWeek) <- c("d_mon", "d_thu", "d_tue", "d_wed")

Ahora creemos de nuevo los correspondientes data.frames incluyendo las variables dummy creadas.

datos_dummies <- subset(datos, select=-c (job, marital, education, 
                                                     default, housing, loan, 
                                                     contact, month, day_of_week))
                       
datos_dummies <- cbind(clean_names(datos_dummies), dummies_job, dummies_marital, 
                       dummies_education, dummies_default, dummies_housing, 
                       dummies_loan, dummies_contact, dummies_month, 
                       dummies_dayWeek )

# Crear la variable dependiente como factor
datos_dummies$y <- relevel(as.factor(datos_dummies$y), ref = "no")

# muestra de estimación
datos_dummies_est <- datos_dummies[est_index,]

# muestra de evaluación
datos_dummies_eval <- datos_dummies[eval_index,]

Y seleccionemos de nuevo el mejor modelo con esta nueva base de datos y con el algoritmo forward.

# modelo sin variables explicativas
min_model_dummies <- glm(y ~ 1, data = datos_dummies_est, family = "binomial")

# modelo con todas las potenciales variables
max_model_dummies <- glm(y ~ ., data = datos_dummies_est, family = "binomial")

# usando forward stepwise para encontrar el mejor modelo
model_forward_dummies <- step(min_model_dummies, 
                              scope = list(lower = min_model_dummies, 
                                           upper = max_model_dummies), 
                              direction = "forward")

El mejor modelo seleccionado es:

summary(model_forward_dummies)

## 
## Call:
## glm(formula = y ~ euribor3m + poutcome + mon_may + mon_mar + 
##     cons_price_idx + cons_conf_idx + c_telephone + emp_var_rate + 
##     d_mon + mon_nov + mon_jun + campaign + def_unknown + j_blue_collar + 
##     mon_aug + j_retired + j_student + mon_oct + d_wed + e_university_degree + 
##     previous + d_thu + j_services, family = "binomial", data = datos_dummies_est)
## 
## Coefficients:
##                       Estimate Std. Error z value Pr(>|z|)    
## (Intercept)         -1.455e+02  9.891e+00 -14.706  < 2e-16 ***
## euribor3m            4.037e-01  8.090e-02   4.990 6.04e-07 ***
## poutcomenonexistent  5.792e-01  9.581e-02   6.045 1.49e-09 ***
## poutcomesuccess      1.737e+00  8.788e-02  19.770  < 2e-16 ***
## mon_may             -5.328e-01  5.978e-02  -8.913  < 2e-16 ***
## mon_mar              1.306e+00  1.123e-01  11.630  < 2e-16 ***
## cons_price_idx       1.522e+00  1.026e-01  14.834  < 2e-16 ***
## cons_conf_idx        1.786e-02  4.885e-03   3.656 0.000256 ***
## c_telephone         -6.623e-01  6.681e-02  -9.914  < 2e-16 ***
## emp_var_rate        -1.263e+00  1.085e-01 -11.640  < 2e-16 ***
## d_mon               -2.264e-01  5.529e-02  -4.096 4.21e-05 ***
## mon_nov             -6.423e-01  8.352e-02  -7.690 1.47e-14 ***
## mon_jun             -5.295e-01  8.539e-02  -6.200 5.63e-10 ***
## campaign            -5.077e-02  1.039e-02  -4.885 1.04e-06 ***
## def_unknown         -2.698e-01  6.283e-02  -4.293 1.76e-05 ***
## j_blue_collar       -1.562e-01  5.962e-02  -2.621 0.008771 ** 
## mon_aug              2.171e-01  8.489e-02   2.557 0.010544 *  
## j_retired            2.888e-01  7.974e-02   3.622 0.000293 ***
## j_student            3.068e-01  9.874e-02   3.107 0.001887 ** 
## mon_oct             -2.911e-01  1.064e-01  -2.736 0.006223 ** 
## d_wed                1.591e-01  5.373e-02   2.960 0.003074 ** 
## e_university_degree  7.210e-02  4.616e-02   1.562 0.118323    
## previous             1.143e-01  5.919e-02   1.932 0.053374 .  
## d_thu                7.974e-02  5.235e-02   1.523 0.127649    
## j_services          -1.150e-01  7.686e-02  -1.496 0.134663    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 23417  on 32949  degrees of freedom
## Residual deviance: 18408  on 32925  degrees of freedom
## AIC: 18458
## 
## Number of Fisher Scoring iterations: 6

Noten que hay una variable no significativa: nr_employed. Eliminémosla.

Veamos este resultado.

summary(model_forward_sel_dummies)

## 
## Call:
## glm(formula = model_forward_dummies$formula, family = "binomial", 
##     data = datos_dummies_est)
## 
## Coefficients:
##                       Estimate Std. Error z value Pr(>|z|)    
## (Intercept)         -1.455e+02  9.891e+00 -14.706  < 2e-16 ***
## euribor3m            4.037e-01  8.090e-02   4.990 6.04e-07 ***
## poutcomenonexistent  5.792e-01  9.581e-02   6.045 1.49e-09 ***
## poutcomesuccess      1.737e+00  8.788e-02  19.770  < 2e-16 ***
## mon_may             -5.328e-01  5.978e-02  -8.913  < 2e-16 ***
## mon_mar              1.306e+00  1.123e-01  11.630  < 2e-16 ***
## cons_price_idx       1.522e+00  1.026e-01  14.834  < 2e-16 ***
## cons_conf_idx        1.786e-02  4.885e-03   3.656 0.000256 ***
## c_telephone         -6.623e-01  6.681e-02  -9.914  < 2e-16 ***
## emp_var_rate        -1.263e+00  1.085e-01 -11.640  < 2e-16 ***
## d_mon               -2.264e-01  5.529e-02  -4.096 4.21e-05 ***
## mon_nov             -6.423e-01  8.352e-02  -7.690 1.47e-14 ***
## mon_jun             -5.295e-01  8.539e-02  -6.200 5.63e-10 ***
## campaign            -5.077e-02  1.039e-02  -4.885 1.04e-06 ***
## def_unknown         -2.698e-01  6.283e-02  -4.293 1.76e-05 ***
## j_blue_collar       -1.562e-01  5.962e-02  -2.621 0.008771 ** 
## mon_aug              2.171e-01  8.489e-02   2.557 0.010544 *  
## j_retired            2.888e-01  7.974e-02   3.622 0.000293 ***
## j_student            3.068e-01  9.874e-02   3.107 0.001887 ** 
## mon_oct             -2.911e-01  1.064e-01  -2.736 0.006223 ** 
## d_wed                1.591e-01  5.373e-02   2.960 0.003074 ** 
## e_university_degree  7.210e-02  4.616e-02   1.562 0.118323    
## previous             1.143e-01  5.919e-02   1.932 0.053374 .  
## d_thu                7.974e-02  5.235e-02   1.523 0.127649    
## j_services          -1.150e-01  7.686e-02  -1.496 0.134663    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 23417  on 32949  degrees of freedom
## Residual deviance: 18408  on 32925  degrees of freedom
## AIC: 18458
## 
## Number of Fisher Scoring iterations: 6

Hagamos lo mismo para el algoritmo backward.

El mejor modelo es:

summary(model_backward_dummies)

## 
## Call:
## glm(formula = y ~ campaign + previous + poutcome + emp_var_rate + 
##     cons_price_idx + cons_conf_idx + euribor3m + j_blue_collar + 
##     j_retired + j_services + j_student + e_university_degree + 
##     def_unknown + c_telephone + mon_aug + mon_jun + mon_mar + 
##     mon_may + mon_nov + mon_oct + d_mon + d_thu + d_wed, family = "binomial", 
##     data = datos_dummies_est)
## 
## Coefficients:
##                       Estimate Std. Error z value Pr(>|z|)    
## (Intercept)         -1.455e+02  9.891e+00 -14.706  < 2e-16 ***
## campaign            -5.077e-02  1.039e-02  -4.885 1.04e-06 ***
## previous             1.143e-01  5.919e-02   1.932 0.053374 .  
## poutcomenonexistent  5.792e-01  9.581e-02   6.045 1.49e-09 ***
## poutcomesuccess      1.737e+00  8.788e-02  19.770  < 2e-16 ***
## emp_var_rate        -1.263e+00  1.085e-01 -11.640  < 2e-16 ***
## cons_price_idx       1.522e+00  1.026e-01  14.834  < 2e-16 ***
## cons_conf_idx        1.786e-02  4.885e-03   3.656 0.000256 ***
## euribor3m            4.037e-01  8.090e-02   4.990 6.04e-07 ***
## j_blue_collar       -1.562e-01  5.962e-02  -2.621 0.008771 ** 
## j_retired            2.888e-01  7.974e-02   3.622 0.000293 ***
## j_services          -1.150e-01  7.686e-02  -1.496 0.134663    
## j_student            3.068e-01  9.874e-02   3.107 0.001887 ** 
## e_university_degree  7.210e-02  4.616e-02   1.562 0.118323    
## def_unknown         -2.698e-01  6.283e-02  -4.293 1.76e-05 ***
## c_telephone         -6.623e-01  6.681e-02  -9.914  < 2e-16 ***
## mon_aug              2.171e-01  8.489e-02   2.557 0.010544 *  
## mon_jun             -5.295e-01  8.539e-02  -6.200 5.63e-10 ***
## mon_mar              1.306e+00  1.123e-01  11.630  < 2e-16 ***
## mon_may             -5.328e-01  5.978e-02  -8.913  < 2e-16 ***
## mon_nov             -6.423e-01  8.352e-02  -7.690 1.47e-14 ***
## mon_oct             -2.911e-01  1.064e-01  -2.736 0.006223 ** 
## d_mon               -2.264e-01  5.529e-02  -4.096 4.21e-05 ***
## d_thu                7.974e-02  5.235e-02   1.523 0.127649    
## d_wed                1.591e-01  5.373e-02   2.960 0.003074 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 23417  on 32949  degrees of freedom
## Residual deviance: 18408  on 32925  degrees of freedom
## AIC: 18458
## 
## Number of Fisher Scoring iterations: 6

Noten que este modelo es exactamente igual al obtenido anteriormente sin la variable no significativa.

Finalmente, empleemos el algoritmo both.

model_backward_dummies <- step(min_model_dummies, 
                           scope = list(lower = min_model_dummies, 
                          upper = max_model_dummies), 
                          direction = "both")

Puedes constatar que este modelo es igual al obtenido por los métodos forward y backward.

De esta manera tenemos 2 modelos para comparar. Por simplicidad llamémoslos modelo1 y modelo2.

modelo1 <- model_forward_sel
modelo2 <- model_forward_sel_dummies

Los resultados de estos dos modelos se presentan en el Cuadro 3.1.

Cuadro 3.1: Modelos Logit estimados
	Modelo 1	Modelo 2
(Intercept)	-143.05^***	-145.46^***
	(10.14)	(9.89)
euribor3m	0.37^***	0.40^***
	(0.08)	(0.08)
monthaug	0.25^*
	(0.11)
monthdec	0.18
	(0.20)
monthjul	0.08
	(0.09)
monthjun	-0.48^***
	(0.10)
monthmar	1.32^***
	(0.12)
monthmay	-0.51^***
	(0.07)
monthnov	-0.59^***
	(0.10)
monthoct	-0.27^*
	(0.12)
monthsep	-0.09
	(0.13)
poutcomenonexistent	0.58^***	0.58^***
	(0.10)	(0.10)
poutcomesuccess	1.74^***	1.74^***
	(0.09)	(0.09)
cons_price_idx	1.50^***	1.52^***
	(0.11)	(0.10)
emp_var_rate	-1.23^***	-1.26^***
	(0.11)	(0.11)
contacttelephone	-0.64^***
	(0.07)
day_of_weekmon	-0.22^***
	(0.06)
day_of_weekthu	0.09
	(0.06)
day_of_weektue	0.01
	(0.06)
day_of_weekwed	0.16^**
	(0.06)
campaign	-0.05^***	-0.05^***
	(0.01)	(0.01)
jobblue-collar	-0.20^**
	(0.06)
jobentrepreneur	-0.02
	(0.12)
jobhousemaid	-0.13
	(0.14)
jobmanagement	0.00
	(0.08)
jobretired	0.25^**
	(0.08)
jobself-employed	-0.04
	(0.11)
jobservices	-0.16
	(0.08)
jobstudent	0.27^**
	(0.10)
jobtechnician	-0.01
	(0.06)
jobunemployed	0.02
	(0.12)
jobunknown	-0.15
	(0.23)
defaultunknown	-0.27^***
	(0.06)
defaultyes	-8.65
	(113.56)
cons_conf_idx	0.02^***	0.02^***
	(0.01)	(0.00)
previous	0.12^*	0.11
	(0.06)	(0.06)
mon_may		-0.53^***
		(0.06)
mon_mar		1.31^***
		(0.11)
c_telephone		-0.66^***
		(0.07)
d_mon		-0.23^***
		(0.06)
mon_nov		-0.64^***
		(0.08)
mon_jun		-0.53^***
		(0.09)
def_unknown		-0.27^***
		(0.06)
j_blue_collar		-0.16^**
		(0.06)
mon_aug		0.22^*
		(0.08)
j_retired		0.29^***
		(0.08)
j_student		0.31^**
		(0.10)
mon_oct		-0.29^**
		(0.11)
d_wed		0.16^**
		(0.05)
e_university_degree		0.07
		(0.05)
d_thu		0.08
		(0.05)
j_services		-0.11
		(0.08)
AIC	18477.92	18458.31
BIC	18780.41	18668.38
Log Likelihood	-9202.96	-9204.15
Deviance	18405.92	18408.31
Num. obs.	32950	32950
^*p < 0.001; ^p < 0.01; ^*p < 0.05

Para terminar, guarda el espacio de trabajo para ser empleado en los siguientes capítulos.

3.4 Comentarios finales

En esta sección hemos discutido sobre uno de los modelos más usados para la tarea de clasificación. Hemos estudiado cómo generar modelos candidatos a ser los mejores modelos empleando estrategias automáticas de selección de variables. En el siguiente capítulo veremos cómo evaluar e interpretar los resultados de modelos Logit. En los próximos capítulos estudiaremos otros modelos estadísticos, así como también métodos de aprendizaje de máquinas.

El modelo Logit, así como los otros modelos que estudiaremos, hace parte de la caja de herramientas de los científicos de datos para realizar la tarea de clasificación. A priori, es imposible saber si emplear el modelo Logit será mejor que los otros y por eso es común que se empleen diferentes aproximaciones y se comparen.

Las aplicaciones de estos métodos de clasificación son muchas en el mundo de los negocios y definitivamente estos modelos son necesarios en la caja de herramientas de un científico de datos.

3.5 Anexos

3.5.1 Demostración de la presencia de Heteroscedasticidad en un Modelo de Probabilidad Lineal

El Modelo de Probabilidad Lineal (MPL) corresponde a un modelo lineal cuya variable dependiente es una dummy. Supongamos que: \[\begin{equation*} P\left[ {{\bf{y}} = 1} \right] = F\left( {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right) \end{equation*}\] \[\begin{equation*} P\left[ {{\bf{y}} = 0} \right] = 1 - F\left( {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right) \end{equation*}\]

Donde, \({{\bf{X}}_{\bf{i}}} = {\left[ {\begin{array}{*{20}{c}} 1 & {{{\bf{X}}_{{\bf{2,i}}}}} & {{{\bf{X}}_{{\bf{3,i}}}}} & \cdots & {{{\bf{X}}_{{\bf{k,i}}}}} \end{array}} \right]_{1 \times k}}\) corresponde a un vector fila con todas las características del individuo \(i\), y \({\beta ^T} = \left[ {\begin{array}{*{20}{c}} {{\beta _1}} & {{\beta _2}} & {{\beta _3}} & \cdots & {{\beta _k}} \end{array}} \right]\). Por tanto, el valor esperado de la variable dependiente será: \[\begin{equation*} E\left[ {{{\bf{y}}_{\bf{i}}}\left| {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right.} \right] = 1 \bullet F\left( {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right) + 0 \bullet \left( {1 - F\left( {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right)} \right) \end{equation*}\] \[\begin{equation*} E\left[ {{{\bf{y}}_{\bf{i}}}\left| {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right.} \right] = F\left( {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right) \end{equation*}\] El MPL implica suponer que \[\begin{equation*} F\left( {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right) = {\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}} = {\beta _1} + {\beta _2}{X_{2,i}} + {\beta _3}{X_{3,i}} + ... + {\beta _k}{X_{k,i}} \end{equation*}\] \[\begin{equation*} F\left( {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right) = {\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}} \end{equation*}\] Así, el modelo que describe el comportamiento de la variable dummy será \[\begin{equation*} {{\bf{y}}_{\bf{i}}} = E\left[ {{{\bf{y}}_{\bf{i}}}\left| {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right.} \right] + {\varepsilon_i} \end{equation*}\] \[\begin{equation*} {{\bf{y}}_{\bf{i}}} = F\left( {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right) + {\varepsilon_i} \end{equation*}\] \[\begin{equation*} {Y_i} = {\beta _1} + {\beta _2}{X_{2,i}} + {\beta _3}{X_{3,i}} + ... + {\beta _k}{X_{k,i}} + {\varepsilon_i} \end{equation*}\] Este modelo lo podemos escribir de forma más compacta de la siguiente manera: \[\begin{equation*} {{\bf{y}}_{\bf{i}}} = {\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}} + {\varepsilon_i} \end{equation*}\]

Supongamos que los errores tienen media cero y no están relacionados. Es decir, \(E\left[ {{\varepsilon_i}} \right] = 0\) y \(E\left[ {{\varepsilon_i},{\varepsilon _j}} \right] = 0 \:\: \forall \:\: i \ne j\). Además, \[\begin{equation*} Y_i = \begin{cases} 1 & \text{ con prob. }F \\ 0 & \text{ con prob. } 1 - F \end{cases} \end{equation*}\]

Por simplicidad escribiremos \(F = F\left( {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right) = {\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}\). Como \(E\left[ {{\varepsilon_i}} \right] = 0\), entonces \(Var\left[ {{\varepsilon_i}} \right] = E\left[ {\varepsilon_i^2} \right] - {\left[ {E\left[ {{\varepsilon_i}} \right]} \right]^2} = E\left[ {\varepsilon_i^2} \right] - 0 = E\left[ {\varepsilon_i^2} \right]\). Así, debemos determinar a qué es igual el valor esperado del error al cuadrado para determinar si éste es constante o no, para saber si es homoscedástico o heteroscedástico.

Noten que, \[\begin{equation*} {{\bf{y}}_{\bf{i}}} = {\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}} + {\varepsilon_i} = \begin{cases} 0 & \text{ con prob. } 1- F \\ 1 & \text{ con prob. } F \end{cases} \end{equation*}\]

Esto implica que el término de error tomará únicamente dos posibles valores dado un vector de características \({\bf{X}}_{\bf{i}}^{\bf{T}}\). Es decir, \[\begin{equation*} \varepsilon_i = \begin{cases} - \beta^T{\bf{X}}_{\bf{i}}^{\bf{T}} & \text{ con prob. } 1- F \\ 1- \beta^T{\bf{X}}_{\bf{i}}^{\bf{T}} & \text{ con prob. } F \end{cases} \end{equation*}\]

Dado que deseamos encontrar la varianza del error y esta corresponde al valor esperado del cuadrado del error (\(Var\left[ {{\varepsilon_i}} \right] = E\left[ {\varepsilon_i^2} \right]\)), entonces tenemos que tener la expresión del cuadrado del error. Es decir, \[\begin{equation*} \varepsilon_i^2 = \begin{cases} \left [ - {\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}} \right ]^2 & \text{ con prob. } 1- F \\ \left [ 1- {\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}} \right ]^2 & \text{ con prob. } F \end{cases} \end{equation*}\] O lo que es lo mismo, \[\begin{equation*} \varepsilon_i^2 = \begin{cases} {\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}} & \text{ con prob. } 1- F \\ 1 - 2{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}} + {\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}} & \text{ con prob. } F \end{cases} \end{equation*}\] Como se trata de una variable discreta, el valor esperado del error al cuadrado corresponderá a: \[\begin{equation*} E\left[ {\varepsilon_i^2} \right] = \left[ {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right]\left[ {1 - F} \right] + \left[ {1 - 2{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}} + {\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right]F \end{equation*}\] \[\begin{equation*} E\left[ {\varepsilon_i^2} \right] = \left[ {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right] - \left[ {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right]F + F - 2\left[ {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right]F + \left[ {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right]F \end{equation*}\] \[\begin{equation*} E\left[ {\varepsilon_i^2} \right] = \left[ {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right] + F - 2\left[ {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right]F \end{equation*}\] Como \(F = {\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}\), tenemos que: \[\begin{equation*} E\left[ {\varepsilon_i^2} \right] = \left[ {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right] + F - 2\left[ {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right]{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}} \end{equation*}\] \[\begin{equation*} E\left[ {\varepsilon_i^2} \right] = F - \left[ {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right] = {\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}} - \left[ {{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}{\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right] \end{equation*}\] \[\begin{equation*} E\left[ {\varepsilon_i^2} \right] = {\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}\left[ {1 - {\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right] \end{equation*}\] Es decir, \[\begin{equation*} Var\left[ {{\varepsilon_i}} \right] = E\left[ {\varepsilon_i^2} \right] = {\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}\left[ {1 - {\beta ^T}{\bf{X}}_{\bf{i}}^{\bf{T}}} \right] \end{equation*}\] \[\begin{equation*} Var\left[ {{\varepsilon_i}} \right] = E\left[ {{{\bf{y}}_{\bf{i}}}\left| {{{\bf{X}}_{\bf{i}}}} \right.} \right]\left[ {1 - E\left[ {{{\bf{y}}_{\bf{i}}}\left| {{{\bf{X}}_{\bf{i}}}} \right.} \right]} \right] \end{equation*}\]

Esto implica que la varianza del error en un modelo de probabilidad lineal depende de cada observación. En otras palabras, por construcción, la varianza del término de error en un modelo de probabilidad lineal no será constante. Por tanto, siempre que la variable dependiente sea una variable dicotómica, un modelo lineal presentará el problema de heteroscedasticidad.

3.5.2 El Modelo Probit

Como se discutió anteriormente, cuando se cuenta con variables dicotómicas como variables dependientes, la probabilidad de observar un valor de uno o cero para una observación depende de la función de distribución que se asuma y más específicamente de su respectiva función de probabilidad acumulativa.

Una función acumulativa que tiene una forma de “S” como la sugerida en el panel c) de la Figura 3.1 es la correspondiente a la distribución normal (ver Figura 3.3). En este caso si suponemos que la función de distribución acumulativa corresponde a una distribución estándar normal tendremos un modelo de elección binario denominado modelo Probit, lo cual implica que: \[\begin{equation} F\left( {{Z_i}} \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{ - {Z_i}} {{e^{ - \frac{{{t^2}}}{2}}}dt} = \Phi \left( { - {Z_i}} \right) \tag{3.6} \end{equation}\]

Entonces los estimadores de Máxima Verosimilitud implicarán resolver el siguiente problema

\[\begin{equation*} \mathop{Max}\limits_\beta \left( \ln \left[ \prod_{\forall y_i = 1}\left ( 1 - \frac{1}{\sqrt {2\pi } }\int_{-\infty }^{-Z_i} e^{-\frac{t^2}{2}dt}\right ) \prod_{\forall y_i = 0} \left ( \frac{1}{\sqrt {2\pi } } \int_{-\infty }^{-Z_i} e^{-\frac{t^2}{2}dt} \right )\right] \right) \end{equation*}\] Esto es equivalente al siguiente problema: \[\begin{equation} \mathop{Max}\limits_\beta \left ( \ln \left [ \prod_{\forall y_i = 1}\left ( 1-\Phi\left ( -Z_i \right ) \right ) \prod_{\forall y_i = 0}\left ( \Phi\left ( -Z_i \right ) \right ) \right ] \right ) \tag{3.7} \end{equation}\]

Figura 3.3: Función de distribución estándar normal (\(f(x)\)) y su correspondiente distribución acumulativa (\(F(x)\))

Fuente: elaboración propia.

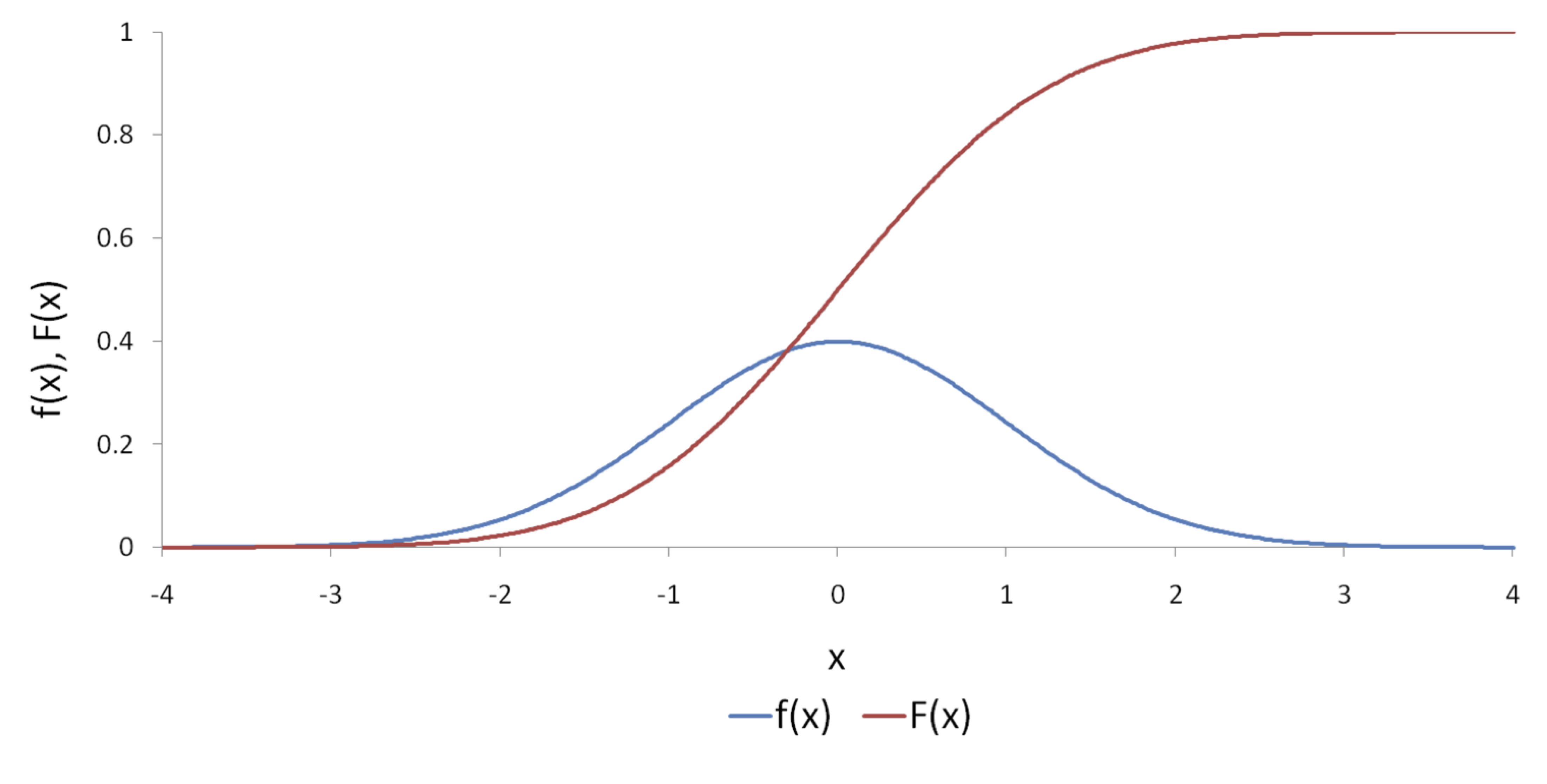
Figura 3.4: Función de distribución acumulativa normal y logística

Fuente: elaboración propia.

Un aspecto importante para resaltar en la estimación de un modelo Probit es que los coeficientes \(\beta\) no tienen interpretación por si solos. Recuerde que una práctica común para interpretar los coeficientes de un modelo es encontrar la derivada del valor esperado de la variable dependiente con respecto a las variables explicativas. En este caso tenemos que: \[\begin{equation*} E\left[ {{{y_i}}\left| {{{{\mathbf{x}}_i}}} \right.} \right] = 1 \bullet \left( {1 - \Phi \left( { {\bf- {Z_i}}} \right)} \right) + 0 \bullet \Phi \left( { {\bf - {Z_i}}} \right) = 1 - \Phi \left( { {\bf - {Z_i}}} \right) \end{equation*}\] Y, por tanto, \[\begin{equation*} \frac{{\partial E\left[ {{{{y}}_{\bf{i}}}\left| {{{{\mathbf{x}}_i}_{\bf{i}}}} \right.} \right]}}{{\partial {{\bf{X}}_{\bf{j}}}}} = - \frac{{\partial \Phi \left( { - {{\bf{Z}}_{\bf{i}}}} \right)}}{{\partial {{\bf{X}}_{\bf{j}}}}}{\beta _j} = \frac{1}{{\sqrt {2\pi } }}{e^{ - \frac{{{\bf{Z}}_{\bf{i}}^{\bf{2}}}}{2}}}{\beta _j} = \phi \left( {{{\bf{Z}}_{\bf{i}}}} \right){\beta _j} \end{equation*}\]

Esto implica que el efecto de un aumento en una unidad en la variable \({X_j}\) provocará un cambio de \(\phi \left( {{Z_i}} \right){\beta _j}\) en la probabilidad de que \({y_i} = 1\). En otras palabras, el efecto marginal de \({X_j}\) no es el mismo para todos los individuos.

Si la muestra es relativamente grande, puede ser muy complicado analizar el efecto marginal de cada una de las variables explicativas para cada uno de los elementos de la muestra. En ese caso una práctica común es calcular todos los efectos marginales para la muestra y calcular el promedio de este. Es decir: \[\begin{equation*} \frac{{\sum\limits_{i = 1}^n {\phi \left( {{Z_i}} \right){\beta _j}} }}{n} \end{equation*}\]

3.5.3 Comentarios sobre los modelos Probit y Logit

La primera diferencia evidente entre emplear un modelo Probit o Logit es el supuesto sobre la distribución empleada. El primero supone una distribución normal mientras que el segundo implica una distribución logística. De hecho la forma de ambas distribuciones acumulativas de probabilidad es muy parecida (Ver Figura 3.4). Esta forma funcional tan parecida hace que exista una relación entre los coeficientes estimados con cada uno de estos modelos para una misma muestra, en especial se tiene que \({\hat \beta _{{\rm{Probit}}}} \approx 0.625{\hat \beta _{{\rm{Logit}}}}\).

Así mismo, los efectos marginales calculados por cada uno de los métodos son relativamente iguales. Por otro lado, no existe ningún método estadístico que permita decidir entre los dos modelos, pues éstos no son comparables.

Finalmente, es importante anotar que el \(LRI\) (Ver siguiente capítulo) no es comparable entre modelos Logit y Probit, pero sí permite comparar modelos Logit entre sí o modelos Probit entre sí.

3.5.4 Selección Automática de Modelos

En la práctica es común que el científico de datos típicamente se encuentre con problemas en los que se conoce claramente la variable que se quiere explicar (variable dependiente) y un conjunto grande de posibles variables explicativas.

En general, si hay \(k-1\) variables independientes potenciales (además del intercepto) que pueden explicar a la variable dependiente, entonces hay \(2^{\left( {k - 1} \right)}\) subconjuntos de variables explicativas posibles para explicar los cambios en la variable dependiente. En la práctica desconocemos cuál de esos modelos es el correcto. Y por tanto tendríamos que probar todos los posibles modelos para encontrar el correcto. Ahora bien, cuando se cuenta con una teoría este problema no existe. Pero en la mayoría de los casos no contamos con teoría que nos apoye en el proceso. Entonces, por ejemplo, si tenemos 10 (\(\left(k-1\right) = 10\)) posibles variables explicativas entonces los posibles modelos serán \({2^{\left( {k - 1} \right)}} = {2^{\left( 10 \right)}} =\) \(1024\). Si se tienen 20 variables candidatas, el número de posibles subconjuntos es de \(1.048576\times 10^{6}\) (más de un millón de posibles modelos). Si son 25 posibles variables, entonces son \(3.3554432\times 10^{7}\). Es decir, aproximadamente 33 millones y medio de posibles modelos.

Así, si se cuenta con muchas variables no es viable calcular todos los posibles modelos. No obstante, si las variables son pocas podría ser viable estimar todos los posibles modelo. Es decir, si no tenemos teoría que soporte el modelaje y tenemos muchas variables, entonces tendremos muchos potenciales modelos a evaluar “manualmente”.

Aquí presentamos diferentes algoritmos para encontrar el mejor modelo de regresión que se ajuste a unos datos determinados cuando se cuenta con un conjunto relativamente grande de posibles variables explicativas.

La idea de la construcción de modelos por pasos es arribar a un modelo de regresión a partir de un conjunto de posibles variables explicativas basados en un criterio que permita adicionar variables (stepwise forward regression) o quitar variables (stepwise backwards regression).

Por ejemplo, supongamos que empleamos un criterio como el valor p de la prueba de significancia individual de cada variable en el modelo. En el primer caso (stepwise forward regression) se parte de un modelo sin variables. Se empieza adicionando al modelo la variable que tenga el mayor valor p. De forma gradual se incluye la siguiente variable que tenga el valor p más grande, se sigue de esta manera hasta que ya no quede ninguna variable para ingresar que sea significativa³⁷.

En el segundo caso (stepwise backwards regression), se parte del modelo con todas las variables y se empieza a eliminar variables que tenga el valor p más bajo. El proceso se repite hasta que no se puedan eliminar variables³⁸. Es fácil imaginarse cómo funcionarán ambos métodos si se emplean criterios como el \(R^2\) ajustado o criterios de información como AIC o BIC. La Figura 3.5 muestra de manera esquemática estas dos aproximaciones.

Figura 3.5: Representación de las estrategias stepwise forward y stepwise backwards

Fuente: elaboración propia.

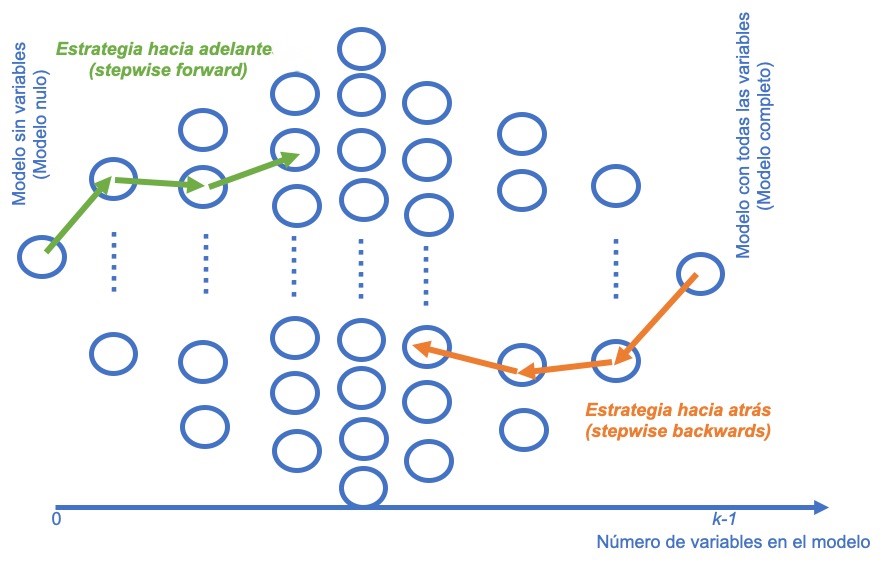
También podemos crear un modelo de regresión a partir de un conjunto de posibles variables explicativas ingresando y eliminando predictores, a este algoritmo se le denomina both.

Referencias

Alonso, J. C. (2024). Introducción al modelo clásico de regresión para científico de datos en r. Universidad Icesi. https://doi.org/XXXX

Batista, G. E., Prati, R. C., & Monard, M. C. (2004). A study of the behavior of several methods for balancing machine learning training data. ACM SIGKDD Explorations Newsletter, 6(1), 20–29.

Chawla, N. V., Bowyer, K. W., Hall, L. O., & Kegelmeyer, W. P. (2002). SMOTE: Synthetic minority over-sampling technique. Journal of Artificial Intelligence Research, 16, 321–357.

Firke, S. (2023). Janitor: Simple tools for examining and cleaning dirty data. https://CRAN.R-project.org/package=janitor

Garcı́a, S., Fernández, A., Luengo, J., & Herrera, F. (2010). Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Information Sciences, 180(10), 2044–2064.

He, H., & Garcia, E. A. (2009). Learning from imbalanced data. IEEE Transactions on Knowledge and Data Engineering, 21(9), 1263–1284.

Kaplan, J. (2023). fastDummies: Fast creation of dummy (binary) columns and rows from categorical variables. https://CRAN.R-project.org/package=fastDummies

Moro, S., Cortez, P., & Rita, P. (2014). A data-driven approach to predict the success of bank telemarketing. Decision Support Systems, 62, 22–31.

R Core Team. (2023). R: A language and environment for statistical computing. R Foundation for Statistical Computing. https://www.R-project.org/

Weiss, G. M., & Provost, F. (2003). Learning when training data are costly: The effect of class distribution on tree induction. Journal of Artificial Intelligence Research, 19, 315–354.

Para una descripción detallada del modelo de regresión clásico ver Alonso (2024).↩︎
Como por ejemplo las unidades demandadas de carros; que si bien no es una variable continua, se supone como tal.↩︎
Para una introducción a las variables dummy y su uso, consultar el Capítulo 5 de Alonso (2024).↩︎
En el apéndice 3.5.1 se presenta una prueba de esta afirmación.↩︎
Es decir, corresponde a la fila \(i\) de la matriz \(\mathbf{x}_i\).↩︎
Es importante anotar que para emplear el método de MCP será necesario emplear como variable ponderadora \(\omega _i^2 = E\left[ {{\bf y_i}\left| {{{\mathbf{x}}_i}} \right.} \right]\left( {1 - E\left[ {{\bf y_i}\left| {{{\mathbf{x}}_i}} \right.} \right]} \right)\). Naturalmente, en el caso del MPL se tiene que \(E\left[ {{y_i}\left| {{{\mathbf{x}}_i}} \right.} \right] = {\beta ^T}{\mathbf{x}}_i^T\). Dado que el vector \(\beta\) no es conocido, es imposible calcular \({\omega _i}\). Esto hace necesario estimar esta variable ponderadora en un primer paso. Así, emplear el método de MCP implicará un primer paso para estimar el modelo original por MCO para obtener \(\hat \beta _{OLS}\). Con estos coeficientes estimados se puede encontrar la variable ponderadora \({W_i} = \sqrt {{{\hat y}_i}\left( {1 - {{\hat y}_i}} \right)}\), donde \({\hat y_i} = {\left( {\hat \beta _{OLS}} \right)^T} {\mathbf{x}}_i^T\). El segundo paso será transformar los datos dividiéndolos por \({W_i}\). El tercer paso implica estimar el modelo por MCO con las variables transformadas.↩︎
También podría emplearse el modelo Probit que es muy similar pero no es tan empleado por los científicos de datos. Los resultados del modelo Probit son muy similares a los del modelo Logit. ↩︎
Recordemos que en el caso de los estimadores MCO, sí existe una fórmula \({({X^T}X)^{ - 1}}{X^T}Y\) que garantiza que al aplicarla la suma de los residuos al cuadrado será mínima. Esa fórmula se denomina estimador.↩︎
Esta forma de distribución es relativamente parecida a la distribución normal que emplea el modelo Probit. Este modelo se presenta en la Sección 3.5.2.↩︎
La base de datos fue descargada del siguiente enlace: https://archive.ics.uci.edu/ml/datasets/Bank+Marketing.↩︎
Los datos se pueden descargar de la página web del libro: http://www.icesi.edu.co/editorial/intro-clasificacion/. ↩︎
Esta variable se define como el número de días que pasaron después de que el cliente fue contactado por última vez desde una campaña anterior. Esta variable fue codificada de tal manera que 999 significa que el cliente no fue contactado previamente. ↩︎
El número de empleado del banco.↩︎
La desviación estándar de esta variable es de 72.3 con una media de 5167, lo que implica un coeficiente de variación de 0.014.↩︎
Esta afirmación es muy discutible. No existe un consenso sobre que umbral debería emplearse para determinar cuándo una muestra se considera desbalanceada, pues puede depender del problema específico y del dominio de aplicación. Sin embargo, algunos autores consideran que una muestra está desbalanceada cuando una clase representa menos del 20% de las observaciones totales (Ver por ejemplo Chawla et al. (2002), Weiss & Provost (2003) y Garcı́a et al. (2010)). Sin embargo, otros autores argumentan que el umbral debería ser 10% (Ver por ejemplo Batista et al. (2004), He & Garcia (2009) y Weiss & Provost (2003)). Por ahora daoptaremos arbitrariamente el umbral del 10%.↩︎
Los generadores de números aleatorios son empleados por el software (como R o cualquier otro) para simular la aleatoriedad que es imposible generar en un computador digital. Es importante tener en cuenta que, en realidad, los números generados por un computador no son verdaderamente aleatorios, ya que se generan utilizando algoritmos deterministas. Estos algoritmos utilizan una “semilla” inicial para producir una secuencia de números aparentemente aleatorios. La calidad de un generador de números aleatorios se evalúa en función de su capacidad para producir secuencias que se asemejen a una secuencia de números verdaderamente aleatorios en términos de distribución y aleatoriedad percibida. Al fijar la semilla, se garantiza que dichos algoritmos siempre generan los mismos números aleatorios.↩︎
Recuerden que la variable duration no es útil para hacer la estimación.↩︎
Para una discusión detallada de los algoritmos de selección automática de variables en el contexto de la regresión múltiple ver Alonso (2024). La filosofía de estos algoritmos es similar al caso del modelo Logit, de tal manera que ese texto puede ser de gran utilidad para aclarar lo que estamos haciendo en este contexto. ↩︎
Noten que esta aproximación tiene un problema práctico difícil de resolver. Se emplean múltiples pruebas individuales que acumulan el error tipo I. No existe almuerzo gratis, este es el costo de emplear esta aproximación.↩︎
Noten que esta aproximación también tiene el problema mencionado para la aproximación forward. No existe almuerzo gratis, este es el costo de emplear esta aproximación.↩︎