13 MATRIZ INSUMO-PRODUCTO
Objetivos del capítulo
Al finalizar este capítulo, el lector estará en capacidad de:
- Entender la estructura y la utilidad de las matrices insumo-producto.
- Distinguir una matriz insumo-producto de una matriz de utilización y de una matriz de oferta.
- Encontrar las relaciones básicas entre valor bruto de la producción, valor agregado, consumo intermedio y demanda final en una matriz insumo-producto.
- Calcular los efectos de cambios en las demandas finales sobre los valores brutos de producción.
- Calcular descomposiciones del producto final en sus valores agregados.
Prerrequisitos: Capítulo 12 (Sistema de cuentas nacionales del DANE: tratamiento de la producción).
Nivel de matemáticas requerido: avanzado.
En el Capítulo 12 se presentó el sistema de descripción de la producción utilizado en el Sistema de Cuentas Nacionales, para lo cual se partió de las cuentas de producción y de bienes y servicios que, organizadas en forma matricial, dan origen a la matriz de insumo-producto. La utilidad de dicha matriz no es solamente la descripción de las transacciones intersectoriales relacionadas con la producción. Con base en esta descripción y algunos supuestos tecnológicos, la matriz insumo-producto puede servir también como herramienta de programación y análisis económico a fin de determinar los niveles de producción que deben alcanzar los diferentes sectores para satisfacer las demandas de consumo o inversión de los diferentes productos; puede utilizarse para estudiar la composición del valor agregado de los productos y efectuar análisis de precios, calcular requerimiento de importaciones, etc. A éstas aplicaciones de la matriz insumo-producto se dedican éste y el siguiente capítulo. Con fines expositivos se utilizará inicialmente una matriz simplificada que difiere en algunos detalles de construcción de la matriz de utilización elaborada por el DANE. Como se observará al final del capítulo siguiente, la matriz del Sistema de Cuentas Nacionales no podría ser utilizada directamente en ejercicios matemáticos de programación, debido a las peculiaridades de su construcción. Sin embargo, el DANE hace los ajustes necesarios y calcula los coeficientes y multiplicadores necesarios para ese propósito.
13.1 Construcción de una matriz insumo-producto simplificada
Sin pérdida alguna de generalidad, para fines expositivos puede trabajarse con una matriz en la que intervienen sólo tres ramas y tres productos y en la que los únicos componentes del valor agregado son los salarios y las ganancias. La inclusión de los impuestos indirectos netos de subsidios y los gastos de depreciación no suponen complicación alguna. Inicialmente se considerará una economía sin transacciones con el exterior (el tratamiento de las exportaciones e importaciones será objeto de estudio del siguiente capítulo). Adicionalmente, se supondrá que existe perfecta correspondencia entre las ramas de producción y los productos y que ninguna rama obtiene productos diferentes a los que le son característicos, es decir, no obtiene producciones secundarias. El tratamiento de las producciones secundarias introduce algunas dificultades, como se discutirá en el capítulo siguiente.
Hechas estas simplificaciones, puede presentarse matricialmente la información proveniente de las cuentas de producción de las ramas y de las cuentas de bienes y servicios (o productos) del Sistema de Cuentas Nacionales. Considérese el Ejemplo 13.1. En sentido vertical, las cuentas de cada rama j expresan una igualdad entre el valor bruto de la producción VBP y los costos incurridos para generarlo, es decir: las compras intermedias (de insumos) a las otras industrias i, \(\sum_i CI_{ij}\) , los pagos de salarios \(S_j\) y las ganancias \(G_j\), que según nuestros supuestos componen la totalidad del valor agregado. Así, cada columna puede ser representada mediante la ecuación
\[V B P_j=\sum_i C I_{i j}+S_j+G_j\]
o, de forma más breve,
\[V B P_j=C I_j+V A_j\]
Ejemplo 13.1
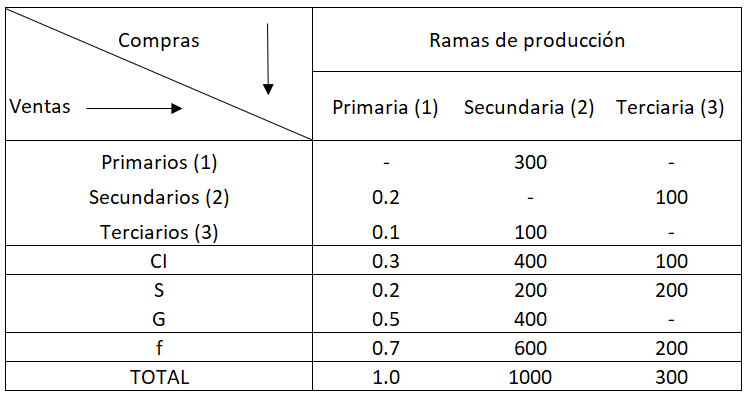
Esquema 13.1 Una matriz sencilla de insumo-producto
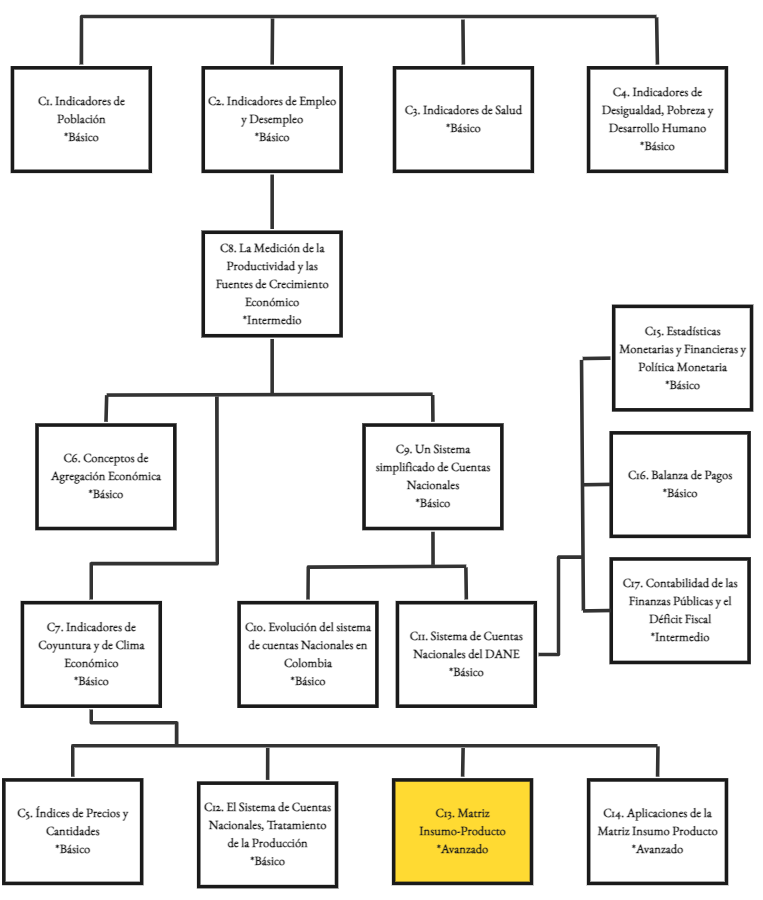
En sentido vertical están las compras que hacen los sectores. Así, el sector primario (rama 1) adquirió insumos industriales por $300, pagó salarios por $100 y obtuvo ganancias por $100, para un valor bruto de la producción de $500. En sentido horizontal están las ventas. Por ejemplo, el sector terciario, o de servicios (3) vendió $100 al sector secundario (para un total de ventas intermedias de $100), y $100 a los consumidores (para un total de ventas de producto final de $100). Nótese que los totales de la columna y la fila de un sector son iguales ($500 en el caso del sector primario), puesto que son dos formas alternativas de calcular el valor bruto de producción del sector.
En sentido horizontal se discriminan los usos dados a cada producción i, los cuales comprenden las ventas intermedias a los otros sectores \(\sum_j CI_{ij}\) , y los usos finales, que en nuestro caso son sólo consumo final \(C_i\) e inversión \(I_i\),
\[O_i=\sum_j C I_{i j}+C_i+I_i\]
donde \(O_i\) es oferta total del producto i. Como no estamos considerando transacciones exteriores ni producciones secundarias, la oferta del producto i equivale a la producción bruta de la rama correspondiente:
\[O_i=V B P_j \text { para } i=j\]
Si se expresa el total de ventas intermedias del sector i a otros sectores como \(V_I\) (lo que es lo mismo que \(\sum_j CI_{ij}\) ), cada fila de la matriz puede expresarse con la igualdad:
\[V B P_i=V I_i+C_i+I_i\]
Así, en el Ejemplo 13.1, el producto del sector primario se destina (como se observa en la fila 1) a consumo intermedio en el sector secundario ($200), consumo final ($200) e inversión ($100). Los usos totales del producto primario que se registran en la última casilla de la fila ($500) son iguales al producto del sector primario como total de la columna correspondiente. De esta manera, para cada columna y fila correspondiente se cumple que
\[C I_j+V A_j=V I_i+C_i+I_i \quad \text { para } \quad i=j\]
Agregando todas las ecuaciones de todos los productos se tiene que
\[\sum_i C I_j+\sum_i V A_j=\sum_i V I_i+\sum_i C I_i+\sum_i I_i\]
Ambos lados de esta ecuación corresponden en el esquema a los totales de todos los valores brutos de producción. Así, la totalidad de compras intermedias entre todos los sectores, \(\sum_j CI_{j}\) es $700, y la suma de valores agregados \(\sum_j VA_{j}\) es $600 para un total de valores brutos de producción de $1,300, lo que a su vez es igual a la totalidad de las ventas intermedias \(\sum_i VI_{i}\) (que son los mismos $700 de las compras intermedias), más la totalidad de los consumos finales \(\sum_i C_{i}\) por $500, más la inversión \(\sum_i I_{i}\) por valor de $100.
Como el conjunto de las ventas intermedias para toda la economía es idéntico a la totalidad de las compras intermedias, la ecuación anterior puede simplificarse a
\[\sum_i V A_j=\sum_i C_i+\sum_i I_i\]
ecuación que expresa sencillamente la igualdad entre el agregado del producto o el ingreso y sus usos finales, esto es, la expresión macroeconómica básica para una economía cerrada:
\[Y=C+I\]
En el ejemplo este valor es de $600, o sea, la suma de los valores agregados, que a su vez corresponden al consumo y la inversión.
13.2 La metodología básica para fines analíticos
13.2.1 Supuestos tecnológicos
El uso de la matriz insumo-producto para fines analíticos depende de la adopción de algunas hipótesis. En el Capítulo 12 se observó que la unidad de clasificación para la descripción de la producción debe ser el establecimiento y no el agente económico o la firma. Se considera que el establecimiento es la unidad de producción más homogénea en cuanto a empleo de recursos y producción. Esta hipótesis de homogeneidad exige que los establecimientos clasificados dentro de cada rama de la producción produzcan un solo producto con la misma estructura de insumos. Para su estricto cumplimiento esta hipótesis requiere que todos los establecimientos dentro de una rama utilicen insumos idénticos y en las mismas proporciones y obtengan también productos idénticos. Como las matrices insumo-producto se elaboran en valores monetarios y no en unidades físicas, el requisito de homogeneidad debe extenderse también a los precios: insumos iguales o productos iguales deben tener precios iguales de valoración para todos los productores. En la práctica, la validez del requisito de homogeneidad depende del número de los sectores y de la precisión con que se definen los productos y sus valoraciones.
La segunda hipótesis que se requiere para aplicar la matriz insumo-producto como herramienta analítica es la existencia de proporcionalidad entre la cantidad de producto de cada sector y las cantidades de insumos y de factores de producción utilizados. El requisito de proporcionalidad implica funciones lineales de producción tales que las necesidades de todos y cada uno de los insumos y factores de producción requeridos en la producción de cada rama varíen proporcionalmente con el volumen de producción. Esto implica que el uso de los insumos y los factores productivos no depende de sus precios relativos, lo cual es un supuesto poco realista y que contradice la lógica de la microeconomía, pues es de esperarse que cualquier recurso que se vuelve más costoso en términos relativos tienda a ser sustituido en alguna medida por otros recursos más baratos. Sin embargo, es preciso mantener este supuesto en un libro introductorio como éste, pues el uso de funciones de producción más realistas, que tengan en cuenta la influencia de los precios relativos, representa complicaciones matemáticas muy importantes. El punto que debe tenerse presente en lo sucesivo es que el supuesto de proporcionalidad sólo tiene sentido siempre que no haya cambios importantes en los precios relativos de los insumos o de los factores productivos.
Como éstas hipótesis dejan en claro, los datos de la matriz son útiles para fines analíticos si reflejan las necesidades tecnológicas de los sectores. Por esta razón, es importante distinguir entre la compra y la utilización de inventarios de materias primas. Para propósitos analíticos interesa registrar en la matriz sólo los usos de insumos, en los cuales se basan los supuestos tecnológicos. Por consiguiente, la acumulación o des-acumulación de inventarios en materias primas debe aparecer como un uso final y no como un uso intermedio del producto.
A lo largo de estos dos capítulos supondremos que se cumplen estas hipótesis tecnológicas y de construcción de la matriz insumo-producto. Al referirnos al final del capítulo siguiente a las modificaciones que deben hacerse a la matriz de utilización del SCN para fines analíticos, señalaremos algunas complicaciones que resultan de violar estos supuestos y cómo debe procederse para obviarlas.
13.2.2 Cálculo de los valores brutos de producción a partir de las demandas finales
Uno de los problemas que puede resolverse a partir de la información que proporciona la matriz insumo-producto es calcular el valor bruto de la producción de cada rama que se requiere para satisfacer un conjunto de necesidades de demanda final de bienes y servicios.
Considérese nuevamente el Ejemplo 13.1. Se necesita una producción bruta total de $1,300 ($500 de la agricultura, $600 de la industria, $200 de servicios) para conseguir un producto final de $600, compuesto así: $300 de bienes primarios, $200 de manufacturas y $100 de servicios. La diferencia entre ambos totales corresponde a las compras intermedias, que son $700 para toda la economía.
Por tanto, podría plantearse la siguiente pregunta: ¿cómo debe modificarse el valor bruto de la producción de cada sector si se desea elevar el consumo de bienes industriales en $100? En principio puede decirse que el VBP industrial deberá también elevarse en $100 para satisfacer la mayor demanda final. Ello significa un aumento del 16.7% sobre el actual VBP industrial, que es de $600. En consecuencia, todas y cada una de las necesidades de insumos del sector industrial tendrían que incrementarse en un 16.7%, como también el valor agregado industrial, debido al supuesto de proporcionalidad enunciado. Ahora bien, como el sector industrial ha aumentado sus compras a los demás sectores, éstos tendrán que elevar también su producto. Así, el sector primario tendrá que elevar su VBP de $500 a $533.3, siendo estos $33.3 lo que ahora el sector secundario va a comprarle de más. Este aumento del VBP agrícola equivale a un 6.6%, porcentaje en el cual deben aumentar sus compras a los otros sectores. Las compras intermedias del sector primario al sector industrial pasarán de $300 a $320 y el valor agregado agrícola de $200 a $213.3. En este punto, sin embargo, el problema se complica, pues al demandar el sector agrícola $20 más del sector industrial, tendríamos nuevamente que modificar el VBP industrial (que habíamos calculado en $700); y con esta modificación aparecerá una nueva demanda de bienes agrícolas por parte del sector industrial y así sucesivamente. Igual cosa sucedería entre el sector industrial y el de servicios y entre éste y el agrícola.
Es posible desarrollar este método de aproximaciones sucesivas, haciendo ajustes en todos los sectores en forma iterativa. Los resultados de las dos primeras iteraciones aparecen en el Ejemplo 13.2, donde las cifras encima de la diagonal en cada casilla resultan de la primera iteración y las de debajo de la segunda.
Ejemplo 13.2
Esquema 13.2 Método iterativo de cálculo del VBP
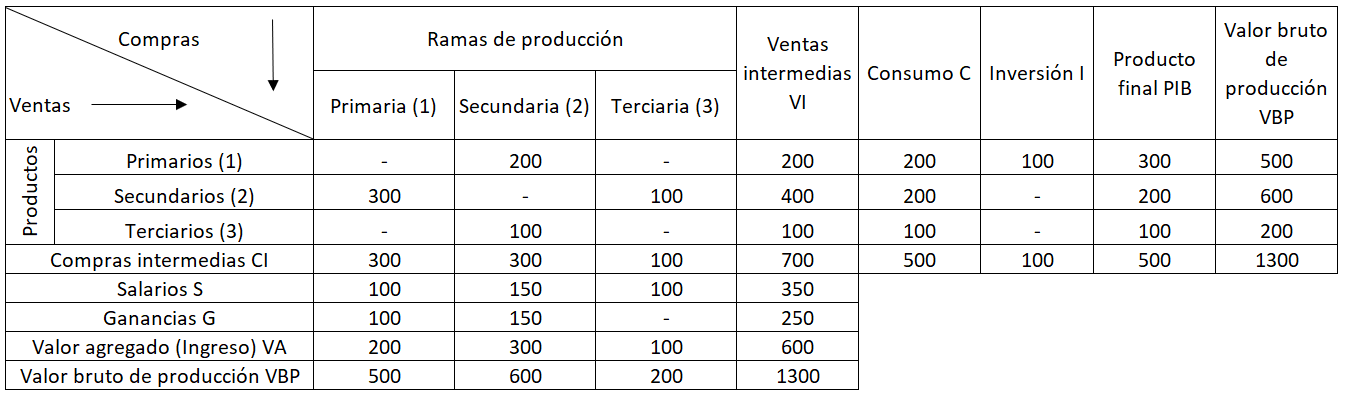
Este ejemplo presenta las dos primeras rondas de re-cálculo de la matriz insumo-producto del Ejemplo 13.1 si la demanda de consumo final (C) del sector secundario fuera 300, en vez de 200, y por lo tanto su valor bruto de producción fuera 700 en vez de 600. En el texto se explican los cálculos paso por paso.
En cada iteración serían menores las correcciones que habría que introducir a cada una de las cifras, de modo que a la quinta o sexta iteración ya estaríamos bastante próximos al resultado final. Entonces el VBP de cada rama tendría que satisfacer tanto las necesidades de demanda final de las que partimos, como las necesidades de insumos requeridos por los otros dos sectores, esto es:
\[V B P_j=C_i+I_i+\sum_j C I_{i j}\]
Como desde un principio hemos supuesto que las necesidades de cada tipo de insumos para cada rama son una proporción constante de su producción, las compras intermedias del insumo i por parte de la industria j pueden expresarse como
\[C I_{i j}=a_{i j} V B P_j\]
donde \(a_{ij}\) es el coeficiente técnico que indica cuáles son las necesidades del insumo por peso de producción bruta del sector j. Si el sector agrícola requiere $300 de insumo industriales para producir un VBP de $500, dicho coeficiente es 0.6. Todos los coeficientes técnicos se calculan dividiendo el valor de las compras intermedias de cada rama por el respectivo VBP de esa rama. Los resultados pueden presentarse en una matriz, que se denomina “matriz de coeficientes técnicos”, tal como la que se presenta en el Ejemplo 13.3, obtenido a partir del Ejemplo 13.1.
Ejemplo 13.3
Esquema 13.3 Matriz de coeficientes técnicos
| Primario (1) | Secundario (2) | Terciario (3) | |
|---|---|---|---|
| Primario (1) | 0.00 | 0.33 | 0.00 |
| Secundario (2) | 0.60 | 0.00 | 0.50 |
| Terciario (3) | 0.00 | 0.17 | 0.00 |
Este ejemplo presenta los coeficientes técnicos, que son simplemente el coeficiente entre las compras de insumos intermedios y el valor bruto de producción del sector que hace la compra, calculados a partir de la matriz insumo-producto del Ejemplo 13.1.
De acuerdo con lo anterior, las ventas intermedias de cada artículo pueden calcularse a partir de estos coeficientes técnicos multiplicados por el VBP de cada sector. Según nuestros datos, las ventas intermedias de bienes primarios deberán ser iguales al 33% del VBP industrial; las de bienes industriales serán el 60% del VBP primario más el 50% del VBP terciario, y las ventas intermedias del sector terciario el 17% del VBP industrial. Entonces, de manera general, las ventas intermedias totales de cualquier sector i son
\[V I_i=\sum_j C I_{i j}=\sum_j a_{i j} V B P_j\]
Como el VBP de cada sector es
\[V B P_i=C_i+I_i+V I_i\]
se tiene entonces que
\[{\huge{\checkmark}}V B P_i=C_i+I_i+\sum_j a_{i j} V B P_j\]
Con esta expresión, los VBP de los tres sectores serán, respectivamente:
\[\begin{aligned} &V B P_1=200+100+\left(0.33 V B P_2\right) \\ &V B P_2=300+\left(0.6 V B P_1+0.5 V B P_3\right) \\ &V B P_3=100+\left(0.17 V B P_2\right) \end{aligned}\]
O, de manera simbólica
\[\begin{aligned} &V B P_1=C_1+I_1+\quad \quad \quad \quad \quad a_{12} V B P_2+ a_{13} V B P_3\\ &V B P_2=C_2+I_2+ a_{21} V B P_1+\quad \quad \quad \quad \quad a_{23} V B P_3\\ &V B P_3=C_3+I_3+ a_{31} V B P_1+ a_{32} V B P_2 \end{aligned}\]
donde los espacios en blanco corresponden a los coeficientes técnicos de cada rama sobre sus propios productos, los cuales son cero.
El sistema anterior consta de tres incógnitas y tres ecuaciones y puede resolverse sin mayor dificultad, como se ve en el Ejemplo 13.4.
Ejemplo 13.4
Queremos calcular los valores brutos de producción utilizando las igualdades entre producción y usos de la producción de cada sector que acabamos de presentar. Para nuestro ejemplo, sustituyendo \(VBP_3\) en la ecuación de \(VBP_2\)
\[V B P_2=300+0.6 V B P_1+0.5\left(100+0.17 V B P_2\right)\]
de donde se deduce que:
\[V B P_2=\frac{350+0.6 V B P_1}{0.915}\]
y reemplazando esto en la ecuación de \(V B P_1\)
\[V B P_1=200+100+0.33 \frac{350+0.6 V B P_1}{0.915}\]
Por consiguiente:
\[\begin{aligned} &V B P_1=543.9 \\ &V B P_2=739.2 \\ &V B P_3=225.7 \end{aligned}\]
También es posible utilizar expresiones matriciales para representar el sistema anterior de ecuaciones:
\[{\huge{\checkmark}}[V B P]_{3 \times 1}=[D]_{3 \times 1}+[A]_{3 \times 3}[V B P]_{3 \times 1}\]
donde \([V B P]\) es el vector columna de los \(V B P_i,[D]\) el vector columna de las demandas finales \(C_i\) e \(I_i\) tomadas conjuntamente y \([A]\) la matriz cuadrada de los coeficientes técnicos \(a_{i j}\), cuyo tamaño en nuestro caso es \(3 \times 3\), como lo señala el subíndice.
Mediante algunas transformaciones (en las cuales [I] es la matriz identidad), se puede despejar el vector \([V B P]\), que es la incógnita del problema:
\[\begin{gathered} {\left[{I]_{3 \times 3}}[V B P]_{3 \times 1}-[A]_{3 \times 3}[V B P]_{3 \times 1}=[D]_{3 \times 1}\right.} \\ {[I-A]_{3 \times 3}[V B P]_{3 \times 1}=[D]_{3 \times 1}} \\ {[V B P]_{3 \times 1}=[I-A]_{3 \times 3}^{-1}[D]_{3 \times 1}} \end{gathered}\]
La matriz \([I-A]\), cuya inversa aparece premultiplicando el vector columna de demanda final \([D]\), se conoce también con el nombre de matriz de Leontief o matriz de requerimientos totales. Fue Wassily Leontief quien inició la construcción de matrices insumo-producto y su empleo para fines de estimación y programación económica
Si se regresa a los datos numéricos del ejemplo, las matrices de la última expresión pueden escribirse como
\[[V B P]_{3 \times 1}=\left[\begin{array}{ccc} 1 & -0.33 & 0 \\ -0.6 & 1 & -0.5 \\ 0 & -0.17 & 1 \end{array}\right]^{-1}\left[\begin{array}{c} 300 \\ 300 \\ 100 \end{array}\right]\]
Calculando la inversa mediante \([I-A]^{-1}=\frac{1}{\operatorname{Det}[I-A]} \operatorname{Adj}[I-A]\)
donde Det es determinante y \(A d j\) adjunta, o sea, transpuesta de cofactores, se tiene que
\[\begin{aligned} {[I-A]^{-1}=\frac{1}{.0717}\left[\begin{array}{ccc} .915 & .330 & .165 \\ .600 & 1.000 & .500 \\ 102 & .170 & .802 \end{array}\right]} \\ =\left[\begin{array}{ccc} 1.276 & 0.460 & 0.230 \\ 0.837 & 1.395 & 0.697 \\ 0.142 & 0.237 & 1.119 \end{array}\right] \end{aligned}\]
de donde los valores de producto buscados son:
\[\left[\begin{array}{l} 543.8 \\ 739.3 \\ 225.7 \end{array}\right]=\left[\begin{array}{lll} 1.276 & 0.460 & 0.230 \\ 0.837 & 1.395 & 0.697 \\ 0.142 & 0.237 & 1.119 \end{array}\right]\left[\begin{array}{l} 300 \\ 300 \\ 100 \end{array}\right]\]
Obsérvese que hemos llegado a los mismos resultados del Ejemplo 13.4, pero ahora mediante un método matricial. La última ecuación representa numéricamente que el valor del producto de cada sector es igual a la sumatoria de los coeficientes de la fila correspondiente, multiplicados por los valores de demanda final, esto es
\[V B P_i=\sum_i r_{i j} D_{i=j}\]
En consecuencia, cada uno de los elementos \(r_{ij}\) de la matriz de Leontief es un coeficiente que indica la cantidad de producto \(VBP_i\) del sector i que se requiere para producir $1 de producto final (\(D_j\)) del sector j. Así, el elemento r23, ubicado en la fila 2 y la columna 3 de la matriz de Leontief, indica el valor de producto del sector 2 requerido para obtener $1 de producto final del sector 3. En nuestro ejemplo, se necesita $0.697 de producto del sector industrial para conseguir $1 de producto final del sector terciario.
Es importante señalar que estos coeficientes \(r_{ij}\) comprenden no sólo los insumos directamente requeridos en la producción de cada bien, sino aquéllos que resultan de las demandas indirectas provenientes de otros sectores, que a su vez aportan insumos para la producción de dicho bien. Como puede verse, cada uno de los coeficientes de la matriz de Leontief es mayor que el correspondiente coeficiente técnico de la matriz original, [A]. Por eso a la matriz de Leontief se la denomina también matriz de requerimientos totales.
Recuadro 13.1 Encadenamientos hacia atrás y hacia adelante
Un resultado muy interesante que se deriva de la matriz de coeficientes técnicos y de la matriz de Leontief son los denominados encadenamientos hacia atrás y hacia adelante de una actividad económica. Los encadenamientos hacia atrás reflejan la importancia relativa de la demanda intermedia, directa e indirecta, del sector j, respecto de la demanda intermedia directa e indirecta de la economía en su conjunto. El encadenamiento directo hacia atrás se mide calculando la suma de los coeficientes de la columna respectiva en la matriz de coeficientes técnicos. El encadenamiento total (que captura los efectos directos e indirectos) se mide realizando la misma operación pero en la matriz de Leontief. Por su parte, los encadenamientos hacia adelante reflejan los estímulos que el sector i proporciona al resto de la economía cuando produce y ofrece un bien que puede emplearse como insumo. De manera análoga, el encadenamiento directo hacia adelante se mide calculando la suma de los coeficientes de la fila respectiva en la matriz de coeficientes técnicos, y el encadenamiento total hacia adelante se mide haciendo la misma operación pero en la matriz de Leontief.
También se puede observar que cada peso de producto final (en cualquier sector) exige en total más de un peso de producción por parte de todos los sectores. Esto no debe extrañar, ya que al sumar entre sí los VBP de los diversos sectores necesarios para producir el producto final, se están contabilizando doblemente algunas compras intermedias que están incluidas en tales VBP. Se puede regresar a los datos originales de la matriz insumo-producto y observar que no hay nada de particular en que la suma de los VBP sea mayor a la suma de los productos finales de toda la economía.
Antes de avanzar en la descripción de las aplicaciones e implicaciones del modelo de programación económica propuesto por Leontief, es importante resaltar un último punto. Nótese que el modelo supone que los niveles de producción de los sectores están completamente determinados por la demanda; ello implica, en otras palabras, que existen excesos de capacidad de producción (o de capacidad instalada) en todos los sectores productivos y oferta laboral disponible para ser utilizada a los salarios existentes, de forma que la producción siempre puede aumentar o disminuir para igualar la demanda sin cambios en los precios.
13.2.3 Descomposición de los productos finales en sus valores agregados
Si del total del valor bruto de la producción se descuentan las compras intermedias, se obtiene el valor del producto final de la economía, que a su vez es igual a la suma de los valores agregados. La matriz insumo-producto permite demostrar que esta igualdad entre el valor agregado rige también para cada producto tomado por separado y no sólo para el total.
Para mostrarlo es preciso calcular primero los coeficientes de valor agregado de cada rama de la producción, los cuales indican qué porcentaje del valor bruto de la producción de cada sector corresponde al valor agregado directamente por el mismo sector. Puesto que el valor agregado se compone de salarios y ganancias, el coeficiente de valor agregado total \(f_j\) de un sector j cualquiera será la suma de sus coeficientes de salarios \(s_j\) y de ganancias \(g_j\) del sector, como se puede ver en el Ejemplo 13.5. En general,
\[ s_j=\frac{S_j}{V B P_j} \]
\[{\huge{\checkmark}}g_j=\frac{G_j}{V B P_j} \] \[f_j=\frac{V A_j}{V B P_j}=s_j+g_j\]
Ejemplo 13.5
Queremos calcular la matriz de coeficientes técnicos y de valor agregado, partiendo de los datos del Ejemplo 13.1. Ya habíamos calculado los coeficientes técnicos en el Ejemplo 13.3. Por su parte, los coeficientes de valor agregado total, incluidos salarios y ganancias, son 0.4, 0.5 y 0.5 para las tres ramas, respectivamente. De acuerdo con estos coeficientes, por cada peso de producto bruto del sector agrícola, por ejemplo, se generan $0.40 de valor agregado directo en dicho sector.
Esquema 13.4 Matriz de coeficientes técnicos y de valor agregado
| Primario | Secundario | Terciario | |
|---|---|---|---|
| Primario (1) | 0.00 | 0.33 | 0.00 |
| Secundario (2) | 0.60 | 0.00 | 0.50 |
| Terciario (3) | 0.00 | 0.17 | 0.00 |
| \(\sum_j a_{ij}\) | 0.60 | 0.50 | 0.50 |
| s | 0.20 | 0.25 | 0.50 |
| g | 0.20 | 0.25 | 0.00 |
| f | 0.40 | 0.50 | 0.50 |
| Total | 1.00 | 1.00 | 1.00 |
Por lo tanto, si los requerimientos de producto bruto necesarios para satisfacer una demanda de producción final se multiplican por estos coeficientes, se tienen como resultado los componentes de valor agregado, libres de duplicaciones, de cada sector en esa producción final. Según los datos de la tercera columna de la matriz \([I – A]^{-1}\) calculada antes, que indican los requerimientos de producción bruta de cada sector por peso de demanda final del sector terciario, para obtener $100 de producción final de ese sector se precisan $23.0 de producción bruta del sector primario, $69.7 del secundario y $111.9 del mismo sector terciario. Si cada uno de estos valores se multiplica por su respectivo coeficiente de valor agregado \(f_j\) y se suman entre sí estos valores, se tiene que
\[\begin{gathered} V A=0.4 \times 23.0+0.5 \times 69.7+0.5 \times 111.9 \\ =100 \end{gathered}\]
con lo cual se muestra que, en efecto, para generar \(\$ 100\) de producto final de sector terciario se requiere en total \(\$ 100\) de valor agregado para toda la economía. Este resultado puede expresarse simbólicamente:
\[V A=\sum_j f_j V B P_j\]
Como ya lo mostramos, la producción bruta que cada sector \(j\) debe generar para satisfacer la demanda final de un sector cualquier \(i\) se calcula como
\[{\huge{\checkmark}}V B P_j=r_{i j} D_i\]
donde \(r_{i j}\) es el término correspondiente en la matriz de Leontief. De modo que si se remplaza en la ecuación anterior, se deduce que
\[V A=\sum_j f_i r_{i j} D_i\]
Pero, según hemos expuesto, el valor agregado es igual a la demanda final; por lo tanto,
\[1=\sum_j f_j r_{i j}\]
Esta expresión rige para todos los sectores y puede escribirse matricialmente como
\[{\huge{\checkmark}}\left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right]=\left[\begin{array}{lll} r_{11} & r_{21} & r_{31} \\ r_{12} & r_{22} & r_{32} \\ r_{13} & r_{23} & r_{33} \end{array}\right]\left[\begin{array}{l} f_1 \\ f_2 \\ f_3 \end{array}\right]\]
La matriz cuadrada que aparece con esta expresión es la transpuesta de \([I-A]^{-1}\), así que en forma abreviada:
\[{\huge{\checkmark}}[1]_{3 \times 1}=\left[(I-A)^{-1}\right]_{3 \times 3}^T[F]_{3 \times 1}\]
El vector columna de unos es igual a la transpuesta de la matriz de Leontief multiplicada por el vector columna de los coeficientes de valor agregado \([F]\). Se aprecia, entonces, que el valor del producto final de cualquier sector puede descomponerse en su totalidad en los valores agregados por los diversos sectores que contribuyen a su producción en forma directa o indirecta. Según veremos en el capítulo siguiente, esta propiedad es de utilidad para análisis de descomposición del ingreso y de precios.
Conceptos clave
| Diferentes matrices |
| Matriz de oferta |
| Matriz de utilización |
| Matriz insumo-producto |
| Matriz de Leontief o matriz de requerimientos totales |
| Matriz transpuesta |
| Métodos de análisis que utilizan la matriz insumo-producto |
| Programación y análisis económico |
| Modelo insumo-producto |
| Agregados económicos que aparecen en la matriz insumo-producto |
| Valor bruto de la producción |
| Salarios |
| Ganancias |
| Valor agregado |
| Consumo intermedio |
| Ventas intermedias |
| Consumo final |
| Inversión |
| Demanda final |
| Oferta total |
| Oferta final |
| Usos finales |
| Conceptos para usar la matriz insumo-producto con fines analíticos |
| Hipótesis de homogeneidad |
| Requisitos de proporcionalidad |
| Coeficiente(s) técnico(s) |
| Coeficientes de valor agregado |
| Descomposición del producto |
| Encadenamientos hacia adelante |
| Encadenamientos hacia atrás |
| Excesos de capacidad |
Preguntas y ejercicios
Pregunta 13.1
Obtenga la matriz insumo-producto completa para la economía de tres sectores que se describe enseguida.
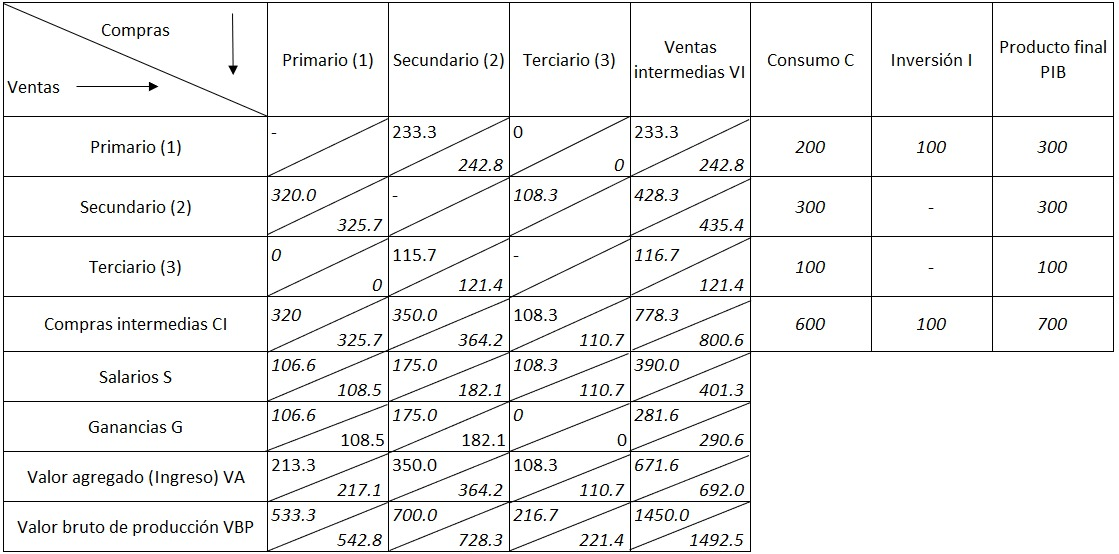
En el año de actividad observado, el sector primario obtuvo una producción bruta de $500, de la cual vendió solamente $400, así: $200 al sector industrial y $200 a los consumidores, ingresos con los cuales cubrió totalmente sus costos antes de ganancias. El sector industrial efectuó compras intermedias por un total de $300 y vendió la totalidad de su producción por un valor bruto de $600, obteniendo ganancias por $150. Dichas ventas se distribuyeron así: $300 a la agricultura, $100 al sector terciario y el resto a los consumidores. Por su parte, el sector terciario obtuvo una producción total por un valor de $200, en la que no hizo ganancia alguna. Por último, el consumo total de bienes finales durante el período analizado fue de $500.
Pregunta 13.2
Obtenga la matriz insumo-producto completa para la economía de tres sectores que se describe enseguida.
En el año de actividad observado, el sector primario adquirió insumos industriales por $100 y pagó servicios por $50. El producto se destinó en su totalidad a la venta, así: $300 al sector industrial y $200 a los consumidores. Una vez cubiertos los costos, los agricultores obtuvieron ganancias por $150. El sector secundario compró, además, servicios por $100, pagó salarios por $200 y obtuvo una producción por valor de $1,000, de los cuales pudo vender $100 a los agricultores, $100 a los productores de servicios y $600 a los consumidores. En cuanto al sector terciario, produjo y vendió servicios por $300 a precios de costo, sin obtener pérdida ni ganancia alguna.
Pregunta 13.3
Obtenga la matriz de coeficientes técnicos y de valor agregado para la matriz insumo-producto del ejercicio anterior.
Pregunta 13.4
Obtenga la matriz de Leontief a partir del punto anterior.
Pregunta 13.5
Con los resultados de los Ejercicios 13.3 y 13.4 calcule los encadenamientos hacia delante y hacia atrás de cada sector. Explique.
Pregunta 13.6
Calcule los requerimientos de valor bruto de la producción de cada uno de los sectores para satisfacer una demanda de bienes finales de $300 del sector primario, $1,000 del sector secundario y $200 del terciario.
Pregunta 13.7
A partir de los resultados del punto anterior demuestre que el valor agregado total es idéntico al valor de los productos finales. Muestre que esto es válido también para cada sector individual.
Pregunta 13.8
Con los resultados de los Ejercicios 13.3 y 13.4 compruebe que \([I]=[I-AT]^{-1} [F]\). Explique por qué tiene que ser así.
Pregunta 13.9
Calcule cómo se distribuye el valor bruto de la producción de cada uno de los tres sectores entre las demandas finales de los tres productos.
Pregunta 13.10
Calcule ahora el destino de los valores brutos distinguiendo en cada demanda final entre consumo e inversión de acuerdo con los datos del Ejercicio 13.2.
Soluciones a ejercicios seleccionados
Las respuestas a todos los ejercicios se pueden ver en los archivos Excel disponibles en el portal del libro.
Respuesta 13.1

Respuesta 13.2
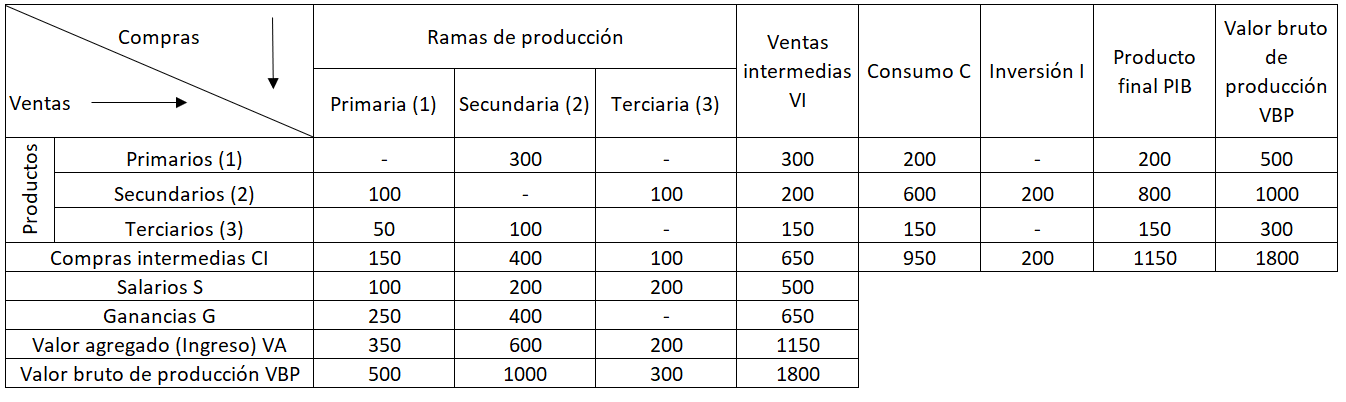
Respuesta 13.3
Respuesta 13.4
Sea \(A\) la matriz de coeficientes técnicos e \(I\) la matriz identidad; entonces
\[[I-A]=\left[\begin{array}{ccc} 1 & -0.3 & 0 \\ -0.2 & 1 & -0.33 \\ -0.1 & -0.1 & 1 \end{array}\right]\]
y su inversa, o sea la matriz de Leontief, o matriz de requerimientos totales será:
\[[I-A]^{-1}=\left[\begin{array}{lll} 1.078 & 0.334 & 0.110 \\ 0.260 & 1.115 & 0.368 \\ 0.134 & 0.145 & 1.048 \end{array}\right]\]
Puede comprobarse que los valores de la inversa son todos positivos y de mayores valores absolutos que los de la matriz original de coeficientes técnicos.
Respuesta 13.6
El vector de producción bruta se calcula como
\[{[V B P]=[I-A]^{-1}[D]}\] \[=\left[\begin{array}{ccc} 1.078 & 0.334 & 0.110 \\ 0.260 & 1.115 & 0.368 \\ 0.134 & 0.145 & 1.048 \end{array}\right]\left[\begin{array}{c} 300 \\ 1,000 \\ 200 \end{array}\right]=\left[\begin{array}{c} 679.9 \\ 1,266.2 \\ 394.6 \end{array}\right]\]
Respuesta 13.7
A nivel agregado el resultado puede obtenerse ajustando los valores brutos de producción arriba obtenidos por los coeficientes de valor agregado respectivos. Matricialmente:
\[\begin{gathered} V A=[V B P]^{\prime}[F] \\ =\left[\begin{array}{lll} 679.9 & 1,266.2 & 394.6 \end{array}\right]\left[\begin{array}{l} 0.70 \\ 0.60 \\ 0.67 \end{array}\right] \\ =1,500 \end{gathered}\]
Los valores agregados totales equivalen al total de demanda final. Lo anterior es válido también para cada sector. Los coeficientes de la matriz de Leontief obtenidos atrás dicen que para obtener un peso de producto final del sector agrícola se requieren \(\$ 1.078\) de producto bruto del mismo sector, \(\$ 0.260\) del sector secundario y \(\$ 0.134\) del terciario. Por lo tanto, para \(\$ 300\) de demanda final se requieren \(\$ 323.4\), \(\$ 77.9\) y \(\$ 40.1\), respectivamente. Aplicando a cada uno de estos valores los respectivos coeficientes de valor agregado y sumando entre sí se tiene que
\[300=0.7 \times 323.4+0.6 \times 78+78+0.67 \times 40.2\]
Respuesta 13.9
Cada elemento \(r_{i j}\) de la matriz \([I-A]^{-1}\) indica la producción bruta del sector \(i\) requerida para satisfacer un peso de demanda final del sector \(j\). Luego, multiplicando cada elemento \(r_{i j}\) por su correspondiente demanda final del sector \(j\) se tendría la descomposición buscada. Matricialmente puede operarse definiendo una matriz cuadrada \([I D]\), cuyos elementos en la diagonal son las demandas finales y los demás elementos son cero. Multiplicando la matriz \([I-A]^{-1}\) por esa nueva matriz \([I D]\) se tiene
\[\left[\begin{array}{ccc} 1.078 & 0.334 & 0.110 \\ 0.260 & 1.115 & 0.368 \\ 0.134 & 0.145 & 1.048 \end{array}\right]\left[\begin{array}{ccc} 300 & 0 & 0 \\ 0 & 1,000 & 0 \\ 0 & 0 & 200 \end{array}\right]=\left[\begin{array}{ccc} 323.4 & 334 & 21.4 \\ 78.0 & 1,115 & 73.6 \\ 40.2 & 145 & 209.6 \end{array}\right]\]
donde cada fila distribuye el valor bruto de la producción de cada sector según su demanda final. Así, la producción bruta total del sector primario (primera fila) tiene los siguientes destinos:
|
$323.4 |
|
$334.0 |
|
$21.4 |
| TOTAL VBP | $678.8 |
NOTA: Véase la bibliografía sobre matrices insumo-producto al final del capítulo siguiente.