1 INDICADORES DE POBLACIÓN
Objetivos del capítulo
Al finalizar este capítulo, el lector estará en capacidad de:
- Entender los principales indicadores que se usan para describir la estructura de la población, su tamaño y su crecimiento.
- Entender la relación entre tasa de crecimiento de la población, tasa de natalidad, tasa bruta de mortalidad y tasa de migración.
- Entender el concepto de tasa específica de mortalidad.
- Comprender el concepto de expectativa de vida y cómo se calcula.
- Saber interpretar una pirámide de población.
- Entender los conceptos de transición demográfica y oportunidad demográfica.
- Tener nociones básicas de cómo se hace una proyección demográfica.
Prerrequisitos: ninguno.
Nivel de matemáticas requerido: básico.
La gente es la base de cualquier economía. La demografía influye en la economía y es influida por ésta a través de numerosos canales. El tamaño de la población en relación con otros recursos incide en cuánto y qué produce una economía. La composición por edades de la población influye en cómo se distribuyen los recursos entre diferentes usos, qué tanto se ahorra y qué tanto pueden aprovecharse las nuevas oportunidades de inversión. Para el crecimiento económico importa no solo el ritmo al que crece la población sino también la composición por edades. A su vez, el crecimiento económico es un determinante central del proceso demográfico.
Por consiguiente, es conveniente empezar este libro de medición económica con una introducción a los indicadores de población. Los demógrafos estudian la composición y el comportamiento de los agregados numéricos de la población. Para ello han diseñado métodos de recolección, selección e interpretación de información, con base en los cuales, tanto directamente como por inferencia, estiman diversos indicadores que permiten describir las características estructurales y el comportamiento de los agregados de población. Este capítulo no intenta abordar todos estos temas. Se limita más bien a introducir los indicadores demográficos más básicos, y a señalar su capacidad descriptiva y sus interrelaciones lógicas. En gran medida se circunscribe al lenguaje básico utilizado por los demógrafos, sin entrar en el estudio de los métodos de recolección, selección, interpretación y corrección de información. El objetivo central de este capítulo es utilizar los indicadores demográficos para describir la dinámica y estructura de la población y para entender cómo se hacen proyecciones demográficas.
1.1 Conceptos demográficos agregados
1.1.1 Tasa de crecimiento de la población y tasa de crecimiento vegetativo
Los cambios en el tamaño de cualquier población son el resultado de tres fenómenos que ocurren a través del tiempo: los nacimientos, las defunciones y la migración. Por tanto, para analizar el comportamiento de la población se puede partir de que ésta, en un momento dado, \(P_1\), es igual a la población en un momento inicial, \(P_0\), más los nacimientos, N, menos las defunciones, D, y más el efecto neto de la inmigración, IN, y la emigración, EM, ocurridos entre esas dos fechas,
\[P_1=P_0 + N - D + (IN-EM)\]
Esta expresión también puede escribirse así:
\[(P_1 - P_0)= (N - D) + (IN-EM)\]
De esta forma se destaca el hecho de que el aumento o disminución de la población resulta de su expansión vegetativa, representada por el primer paréntesis de la derecha, y de los fenómenos migratorios, resumidos en el segundo paréntesis. Si las fechas de comparación utilizadas como períodos 0 y 1 corresponden a dos años sucesivos, la ecuación anterior puede expresarse en términos de tasas anuales. Para ello, todos los términos de la ecuación se dividen por la población inicial (o por la población en una fecha intermedia entre los dos momentos) y se multiplican, para facilitar la computación, por 1,000 (u otra constante),
\[\frac{(P_1 - P_0)}{P_0} \times 1,000= \frac{(N - D)}{P_0}\times1,000 + \frac{(IN-EM)}{P_0}\times1,000\]
Por tanto, la tasa de crecimiento de la población, TCP, es igual a la tasa de crecimiento vegetativo, TCV, más la tasa neta de migración, TNM (todas expresadas en términos anuales por cada 1,000 habitantes),
\[{\huge{\checkmark}} TCP= TCV + TNM\]
Ejemplo 1.1 – Cómo usar la formula TCP = TCV + TNM
Suponga que cuenta con la siguiente información:
La población al 31 de diciembre del año 0, \(P_0\) = 7,850,000
Los nacimientos durante el año 1, N = 250,000
Las defunciones durante el año 1, D = 150,000
El efecto neto de inmigración durante el año 1 es de (IN-EM) = -20,000 personas
La emigración es EM = 70,000
Primero se obtiene la población para el 31 de diciembre del año 1, y para ello basta con reemplazar los valores que se tienen:
\[P_1= 7,850,000 + 250,000 - 150,000 - 20,000\]
\[P_1= 7,930,000\]
Para obtener la inmigración (IN):
\[(IN-EM)= -20,000\]
\[IN= EM -20,000\]
\[IN= 70,000 - 20,000 = 50,000\]
Vale la pena aclarar que no era necesario obtener el número de inmigrantes, puesto que ya se tenía el efecto neto de migración. Ahora, utilizando la fórmula de las tasas, se tiene que:
\[\frac{(P_1 - P_0)}{P_0}\times1000= \frac{(N - D)}{P_0}\times1000 + \frac{(IN-EM)}{P_0}\times1000\]
\[\frac{7,930,000-7,850,000}{7,850,000}\times1,000=\frac{250,000-150,000}{7,850,000}\times1,000+\]
\[\frac{50,000-70,000}{7,850,000}\times1,000\]
\[10.2=12.7-2.5\]
El término a la izquierda de la equivalencia corresponde a la tasa de crecimiento poblacional. En este caso hipotético la tasa de crecimiento poblacional fue de 10.2 personas por cada 1,000 individuos, explicada por una tasa de crecimiento vegetativo de 12.7 personas por cada 1,000 habitantes menos una tasa neta de migración de 2.5 personas por cada 1,000 habitantes.
Vale la pena introducir aquí dos conceptos muy sencillos de uso común en economía: saldos y flujos. Un saldo (acervo, o stock, como a menudo se dice con esa tendencia de los economistas a utilizar expresiones prestadas del inglés) es cualquier variable que se mide en un momento del tiempo; mientras que un flujo es una variable que se mide durante un período, es decir entre dos momentos del tiempo. (¿Cuáles de las variables anteriores son saldos y cuáles flujos?).
1.1.2 Tasas brutas de natalidad y mortalidad
Puesto que el incremento vegetativo de la población es la diferencia entre los nacimientos y las defunciones, también puede establecerse que
\[\frac{(P_1 - P_0)}{P_0}\times1,000= \frac{N}{P_0}\times1,000 - \frac{D}{P_0}\times1,000 + \frac{(IN-EM)}{P_0}\times1,000\]
o de forma más abreviada,
\[TCP= TBN - TBM + TNM\]
Así, la tasa de crecimiento de la población, TCP, equivale a la diferencia entre la tasa bruta de natalidad, TBN, y la tasa bruta de mortalidad, TBM, más la tasa neta de migración, TNM, expresadas todas por cada 1,000 habitantes y por año.
1.1.3 La transición demográfica
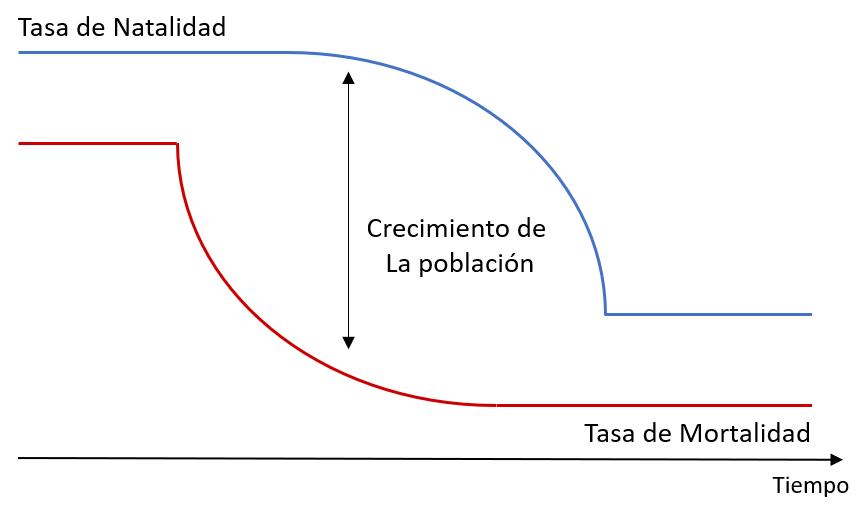
La población mundial creció en el siglo XX a una tasa mayor que en ningún otro período. Este crecimiento fue el resultado del proceso de transición demográfica que afectó a casi todos los países y que, en muchos casos, aún no ha concluido. Se entiende por transición demográfica el proceso de cambio demográfico desde una situación de altas tasas de natalidad y mortalidad a otra de bajas tasas de natalidad y mortalidad. Típicamente, ese proceso comienza con una caída de la tasa de mortalidad (generalmente como resultado de mejores condiciones sanitarias), que después de un tiempo viene seguido de una reducción de las tasas de natalidad. El desfase entre estos dos procesos significa que la tasa de crecimiento de la población aumenta primero, y luego se reduce gradualmente a medida que se avanza en el proceso de transición demográfica (Gráfico 1.1). El estado de la transición y la velocidad con la que ha ocurrido, determina el tamaño relativo de cada generación.
Gráfico 1.1 Transición demográfica
Gráfico 1.1: Transición demográfica
Para Colombia (Gráfico 1.2) la TBN pasó de 46.11 en 1960 a 14.65 en 2019, y la TBM pasó de 11.67 en 1960 a 5.63 en 2019 (este gráfico puede verse de manera interactiva en la versión HTML del libro).
Fuente: Banco Mundial
1.2 Conceptos demográficos por grupos de edad
1.2.1 Índices específicos de mortalidad
Una vez se ha descompuesto el crecimiento de la población en sus tres fuentes de cambio –mortalidad, natalidad y migración–, cada uno de dichos fenómenos puede descomponerse, a su vez, según su incidencia entre los grupos que conforman la población. Dado que se trata de fenómenos determinados que afectan con distinta intensidad a los diferentes grupos de población clasificados según edades y sexo, es útil distinguir las tasas específicas de ocurrencia de tales fenómenos para cada uno de los grupos de población. En el caso de la mortalidad, todos los grupos de edad y sexo están expuestos a esa contingencia, de suerte que la tasa bruta de mortalidad es un resultado de las tasas específicas de mortalidad de estos grupos. Una tasa específica de mortalidad indica el número de muertes durante un año por cada 1,000 habitantes dentro de una cierta franja de edades. La tasa bruta de mortalidad puede verse así como el promedio ponderado de esas tasas específicas, donde la ponderación es el tamaño relativo de la población de cada uno de esos grupos,
\[{\huge{\checkmark}}TBM=\sum_i{TEM_i \frac{P_i}{P}}\]
donde \(TEM_{i}\) son las tasas específicas de mortalidad, siendo \(i\) una franja de edades, como 0-4 años, 5-9 años, etcétera, y \(P_i\) las poblaciones existentes dentro de las mismas franjas que, al ser divididas por la población total, \(P\), quedan convertidas en coeficientes de ponderación (por supuesto, si se sumaran todos los coeficientes de ponderación, el total sería 1).
Es común especificar las tasas de mortalidad de cada franja de edades según sexo, ya que, por razones naturales y de comportamiento, existen diferencias sistemáticas entre las tasas de mortalidad masculina y femenina en cada rango de edad (las segundas son usualmente menores).
Cabe señalar que las tasas específicas de mortalidad son indicativas de las condiciones de salud y nutrición y que sus cambios son sintomáticos de transformaciones económicas, sociales y culturales de la población. Por eso son útiles como indicadores de calidad de la salud y de nivel de vida, según veremos en el Capítulos 3 y 4.
Ejemplo 1.3 – Cálculo de la tasa bruta de mortalidad
Se cuenta con la siguiente información de defunciones totales por grupos de edad en Colombia para el 2021:
Defunciones totales por grupos de edad en Colombia (2021)
| Grupo | Defunciones no fetales | Población |
|---|---|---|
| De 0 a 4 años | 8,147 | 3,922,169 |
| De 5 a 9 años | 835 | 3,957,795 |
| De 10 a 14 años | 1,223 | 3,973,505 |
| De 15 a 19 años | 3,699 | 4,102,336 |
| De 20 a 24 años | 6,690 | 4,312,904 |
| De 25 a 29 años | 7,509 | 4,288,150 |
| De 30 a 34 años | 7,633 | 3,954,276 |
| De 35 a 39 años | 8,609 | 3,661,744 |
| De 40 a 44 años | 10,394 | 3,320,634 |
| De 45 a 49 años | 12,096 | 2,941,686 |
| De 50 a 54 años | 16,612 | 2,848,466 |
| De 55 a 59 años | 23,111 | 2,657,919 |
| De 60 a 64 años | 30,076 | 2,229,425 |
| De 65 a 69 años | 34,115 | 1,723,800 |
| De 70 a 74 años | 37,897 | 1,257,119 |
| De 75 a 79 años | 38,664 | 847,828 |
| De 80 y más | 115,765 | 1,049,742 |
| Total | 363,075 | 51,049,498 |
El primer paso para calcular la tasa bruta de mortalidad es obtener las tasas específicas de mortalidad. Para eso, se divide el número de defunciones en un rango de edad por el número total de personas en ese mismo rango de edad y ese valor se multiplica por 1,000 para obtener la \(TEM_i\). Luego se multiplican las tasas de mortalidad específicas por el ponderador \(\frac{P_i}{P}\):
Cálculo de la tasa bruta de mortalidad
| Grupo de edad | \(Defunciones/P_{i}\) | \(TEM_{i}\) | \(P_{i}/P\) | \(TEM_{i}\times(P_{i}/P)\) |
|---|---|---|---|---|
| De 0 a 4 años | =(8,147/3,922,169) | 2.08 | 0.08 | 0.16 |
| De 5 a 9 años | =(835/3,957,795) | 0.21 | 0.08 | 0.02 |
| De 10 a 14 años | =(1,223/3,973,505) | 0.31 | 0.08 | 0.02 |
| De 15 a 19 años | =(3,699/4,102,336) | 0.90 | 0.08 | 0.07 |
| De 20 a 24 años | =(6,690/4,312,904) | 1.55 | 0.08 | 0.13 |
| De 25 a 29 años | =(7,509/4,288,150) | 1.75 | 0.08 | 0.15 |
| De 30 a 34 años | =(7,633/3,954,276) | 1.93 | 0.08 | 0.15 |
| De 35 a 39 años | =(8,609/3,661,744) | 2.35 | 0.07 | 0.17 |
| De 40 a 44 años | =(10,394/3,320,634) | 3.13 | 0.07 | 0.20 |
| De 45 a 49 años | =(12,096/2,941,686) | 4.11 | 0.06 | 0.24 |
| De 50 a 54 años | =(16,612/2,848,466) | 5.83 | 0.06 | 0.33 |
| De 55 a 59 años | =(23,111/2,657,919) | 8.70 | 0.05 | 0.45 |
| De 60 a 64 años | =(30,076/2,229,425) | 13.49 | 0.04 | 0.59 |
| De 65 a 69 años | =(34,115/1,723,800) | 19.79 | 0.03 | 0.67 |
| De 70 a 74 años | =(37,897/1,257,119) | 30.15 | 0.02 | 0.74 |
| De 75 a 79 años | =(38,664/847,828) | 45.60 | 0.02 | 0.76 |
| De 80 y más | =(115,765/1,049,742) | 110.28 | 0.02 | 2.27 |
| Total | =(363,075/51,049,498) | 7.11 | 1.00 | 7.11 |
La tasa bruta de mortalidad se obtiene al sumar las multiplicaciones de las tasas específicas de mortalidad (la última columna del cuadro anterior). En este caso:
\[TBM=\sum_i{TEM_i \frac{P_i}{P}}=7.11\]
Otra alternativa para obtener la Tasa Bruta de Mortalidad consiste en dividir el número total de defunciones por la población total del país y multiplicarlo por 1,000, es decir:
prettyNum(info_ejemplo_1.3$Población, big.mark = “,”, scientific = FALSE)
\[TBM=\frac{363,075}{51,049,498}\times1,000=7.11\]
1.2.2 Expectativa de vida
A partir de un conjunto de tasas específicas de mortalidad se puede determinar la esperanza o expectativa de vida \(e^o_x\) , es decir, el promedio matemático de años adicionales que una persona o un grupo demográfico homogéneo podría aspirar a vivir a partir de una edad dada x, en caso de prevalecer las condiciones de mortalidad existentes. La expectativa de vida al nacer es la más utilizada, y se define como:
\[{\huge{\checkmark}} e^o_0=\sum_i{\frac{L_i}{I_0}}\]
donde \(L_i\) son los años de vida aportados por los sobrevivientes al comienzo de cada período y \(I_0\) es el número de individuos que conforman la cohorte inicial de recién nacidos. Por consiguiente, para calcular una expectativa de vida simplemente se necesita establecer cuántos años de vida aportan cada año quienes comienzan vivos ese año. Luego se agregan todos los años de vida aportados y se divide el total por el tamaño de la cohorte inicial.
En la práctica los demógrafos trabajan también con rangos diferentes a un año, pero por el momento se puede ignorar esta complicación. Supóngase entonces que se conocen las tasas específicas de mortalidad para rangos de edad de un año y que se desea calcular la expectativa de vida de una cohorte de mil recién nacidos (donde, nuevamente, 1,000 es un número arbitrario escogido para facilitar los cálculos). Durante el primer año esta cohorte enfrentará un riesgo de mortalidad, dado por la tasa específica de mortalidad entre 0 y 1 años, \(TEM_{0-1}\), de suerte que se producirá un número de muertes durante el primer año igual a \(TEM_{0-1}\) (puesto que esta tasa viene dada por cada mil individuos). Al concluir el primer año, el conjunto de los individuos vivos en el período 0 (es decir, la cohorte de los 1,000 recién nacidos) habrá aportado el siguiente número de personas-años de vida:
\[L_0=(TEM_{0-1}\times0.3)+(1,000-TEM_{0-1})\]
donde el primer paréntesis representa el número de personas-años aportados por quienes mueren durante su primer año de vida, y el segundo el que aportan los sobrevivientes. Por ejemplo, si la tasa de mortalidad infantil \(TEM_{0-1}\) fuera 25 por cada mil, los años de vida aportados durante el primer año por la cohorte inicial de mil nacidos vivos serían 982.5 años.
\[L_0=(25\times0.3)+(1,000-25)=7.5+975=982.5\]
Obsérvese que, de acuerdo con esta expresión, la edad promedio de vida alcanzada por quienes mueren en el primer año es de 0.3 años, debido a que las muertes tienden a concentrarse en los meses iniciales de vida en vez de distribuirse homogéneamente a lo largo de todos los meses, caso en el cual el promedio sería de 0.5.
A fin de simplificar la notación para el cálculo sucesivo de las personas-años de vida, puede expresarse el número de sobrevivientes al final de los años \(i\) de vida, \(I_i\), como el producto del número de individuos sobrevivientes al final de los años \(i-1\) de vida, \(I_{i-1}\), y la probabilidad de que sobrevivan durante el año (probabilidad que es igual a 1 menos la respectiva tasa específica de mortalidad para esa edad):
\[I_i=I_{i-1}\times (1-\frac{TEM_{((i-1)-i)}}{1,000})\]
Con la \(TEM_{0-1}\) de 25 que hemos supuesto, esto significa que \(I_1\) es 975.
\[I_1=1,000\times(1-\frac{25}{1,000})=1,000\times(1-0.025)=975\]
Según esta notación, la ecuación que representa el número de personas-años de vida en el primer año, presentada arriba, puede escribirse también como:
\[L_0=(I_0-I_1 )\times0.3+I_1\]
\[L_0=(1,000-975)\times0.3+975=982.5\]
Puede comprobarse nuevamente que con la tasa de mortalidad infantil supuesta (25 por mil), el número de años de vida aportados por la cohorte en ese primer año es 982.5. Al año siguiente, el conjunto de individuos de la cohorte aportará un número de personas-años de vida equivalente a
\[L_1=(I_1-I_2)\times 0.4 + I_2\]
donde el primer sumando representa los años aportados por quienes mueren a lo largo del año y el segundo el número de años aportados por quienes sobreviven. Nótese nuevamente que la constante 0.4 implica que las muertes de los niños en su segundo año de vida también tienden a concentrarse en los primeros meses del año, aunque menos que en el caso anterior. En los años sucesivos, puede suponerse que las muertes se distribuyen a lo largo del año, y por tanto:
\[L_{i-1}=(I_{i-1}-I_i )\times0.5+I_i , \: i \geq 3\]
\[=0.5I_{i-1}+0.5I_i\]
\[=\frac{(I_{i-1}+I_i)}{2}\]
Por consiguiente, a partir del tercer año, los años de vida aportados son un promedio simple del número de personas que comienzan y el número de personas que sobreviven al final de cada período. Este proceso puede continuarse hasta cuando no queden sobrevivientes (o terminarse arbitrariamente fijando una edad límite de vida). Agregando finalmente todos los L y dividiendo por el número inicial de personas de la cohorte, se obtiene entonces la expectativa de vida al nacer, como se había definido:
\[{\huge{\checkmark}}e^o_0=\sum_i{\frac{L_i}{I_0}}\]
Como puede observarse, el cálculo de una expectativa de vida es un proceso iterativo que permite obtener, a partir de tasas específicas de mortalidad y un tamaño arbitrario de una cohorte inicial, los siguientes valores para cada rango sucesivo de edad:
- Número de sobrevivientes al principio de cada intervalo.
- Número de muertes durante cada intervalo de edad.
- Número de personas-año de vida aportados por quienes viven y mueren dentro de cada intervalo de edad.
- Número de personas-año de vida aportados por quienes sobreviven cada intervalo de edad.
Los demógrafos recopilan toda esta información en “tablas de vida”, normalmente utilizando rangos de un año solamente para el primer o dos primeros años de vida, y a partir de ahí rangos mayores, usualmente de cinco años. El mismo método utilizado para calcular la expectativa de vida al nacer puede servir para obtener expectativas de vida para otras edades, entendiéndose por ellas el número de años esperados que restan por vivir a una cohorte de individuos de una cierta edad, en caso de que prevalezcan las condiciones de mortalidad existentes en el momento para los diferentes rangos de edad.
Ejemplo 1.4 - Cálculo de la expectativa de vida
La forma de cálculo de la expectativa de vida es un proceso iterativo que se puede programar fácilmente en una hoja de cálculo como se muestra en este cuadro:
| Grupo de edad | \(TEM\times1,000\) | \(I_i\) | \((I_0-I_1)\times F\) | \(L_i\) |
|---|---|---|---|---|
| De 0 a 1 | 25 | \(1,000 *(1-(\frac{25}{1,000})) = 975\) | \((1,000-975)*0.3 = 7.5\) | \(975+7.5 = 982.5\) |
| De 1 a 2 | 15 | \(975*(1-(\frac{15}{1,000})) = 960.4\) | \((975-960.4)*0.4=5.9\) | \(960+5.9 = 966.2\) |
| De 2 a 3 | 7 | \(960.4*(1-(\frac{7}{1,000})) = 953.7\) | \((960.4-953.7)*0.5=3.4\) | \(953.7+3.4 = 957.0\) |
| De 3 a 4 | 4 | \(953.7*(1-(\frac{4}{1,000}))=949.8\) | \((953.7-949.8)*0.5=1.9\) | \(949.8 + 1.9= 951.7\) |
| De 4 a 5 | 4 | \(949.8*(1-(\frac{4}{1,000}))=946.0\) | \((949.8-946)*0.5=1.9\) | \(946 + 1.9 = 947.9\) |
Extendiendo las filas del cuadro hasta una cierta edad, la expectativa de vida hasta esa edad se calcula sumando todos los valores de la columna \(L_i\) y dividiendo dicha suma entre el número de personas inicial, así:
\[EV=\frac{(982.5+966.2+957.0+951.7+947.9)}{1,000}=4.8\]
En este caso, como la tabla sólo llega hasta los cinco años, el valor de 4.8 años puede interpretarse como el número de años esperados por vivir en los primeros cinco años de vida para una cohorte de individuos recién nacidos en caso de que prevalezcan las condiciones de mortalidad existentes en el momento para los diferentes rangos de edad. Si se extienden las filas del cuadro hasta que ya no quede ningún sobreviviente, el resultado será la expectativa de vida total de esa cohorte.
1.2.3 Índices de fecundidad específicos por edades y tasa de fecundidad general
Como se ha visto, la tasa bruta de mortalidad es el resultado de un conjunto de tasas específicas de mortalidad por grupos de edad. De igual forma, la tasa bruta de natalidad puede verse como el resultado de un conjunto de tasas específicas de fecundidad para los diferentes grupos de edad femeninos o masculinos de la población. Por razones prácticas de obtención de información, las tasas de fecundidad más corrientemente utilizadas son las femeninas, que se calculan para las mujeres en edad de procrear, entre los 15 y 49 años. De esta forma una tasa específica de fecundidad, para el grupo de mujeres dentro del rango de edad i, \(TEF_i\) , se define como el número de hijos nacidos en un año de cada 1,000 mujeres en ese rango de edad:
\[TEF_i=\frac{N_i}{P_{fi}} \times1,000\]
A partir del conjunto de \(TEF\) puede obtenerse la tasa bruta de natalidad según la siguiente expresión:
\[TBN=\sum_iTEF_i \frac{ P_{fi}}{P} \]
Obsérvese que los factores de ponderación de cada una de las \(TEF\) son las proporciones entre el número de mujeres en el rango de edad respectivo y la población total, femenina y masculina. Esto es así porque la TBN se define como una proporción entre nacimientos totales y población total, lo cual es equivalente a la expresión anterior, como puede deducirse remplazando la definición de \(TEF\):
\[TBN=\sum_i\frac{N_i}{P_{fi}} \times1,000\frac{P_{fi}}{P}\]
\[=\sum_i\frac{N_i}{P}\times1,000\]
Sin embargo, con base en las \(TFE\) puede obtenerse también una medida de fecundidad referida solamente al grupo de las mujeres en edad procreativa. Se trata de la tasa de fecundidad general, \(TFG\), que se define como el número de nacimientos por cada 1,000 mujeres entre los 15 y 49 años:
\[TFG=\frac{N}{P_{f 15-49}} \times1,000\]
La \(TFG\) puede también expresarse a partir de las tasas específicas de fecundidad, ponderadas en este caso por la participación de cada grupo de edad en el número total de mujeres en edad de procrear,
\[{\huge{\checkmark}}TFG=\sum_iTEF_i\frac{P_{fi}}{P_{f 15-49}}\]
Por consiguiente, la tasa de fecundidad general puede variar, no sólo debido a cambios en los patrones de fecundidad de cada grupo de edad sino, también, por los cambios en la distribución por edades de las mujeres en edad procreativa.
Ejemplo 1.5 - Cálculo de la tasa de fecundidad general
Se cuenta con información de Colombia para 2021 de los nacimientos y la población de mujeres por grupos de edad y se quiere calcular la tasa de fecundidad general (\(TFG\)).
El primer paso consiste en calcular las tasas de fecundidad específicas para cada grupo poblacional de mujeres (\(TEF_i\)) utilizando la siguiente fórmula,
\[TEF_i=\frac{N_i}{P_{fi}} \times1,000 \]
| Grupo edad madre | Nacimientos | Población de mujeres | \(Nacimientos/P_{fi}*1000\) | \(TEF_i\) | \(P_{fi}/P_{f15-49}\) | \(TEF_i * (P_{fi}/P_{f15-49})\) |
|---|---|---|---|---|---|---|
| De 15 a 19 años | 107,741 | 2,016,401 | \(=(\frac{107,741}{2,016,401})* 1,000\) | 53.43 | 0.15 | 8.00 |
| De 20 a 24 años | 175,376 | 2,139,671 | \(=(\frac{175,376}{2,139,671})* 1,000\) | 81.96 | 0.16 | 13.02 |
| De 25 a 29 años | 154,019 | 2,152,858 | \(=(\frac{154,019}{2,152,858})* 1,000\) | 71.54 | 0.16 | 11.43 |
| De 30 a 34 años | 103,612 | 2,007,982 | \(=(\frac{103,612}{2,007,982})* 1,000\) | 51.60 | 0.15 | 7.69 |
| De 35 a 39 años | 54,963 | 1,879,454 | \(=(\frac{54,963}{1,879,454})* 1,000\) | 29.24 | 0.14 | 4.08 |
| De 40 a 44 años | 14,798 | 1,725,658 | \(=(\frac{14,798}{1,725,658})* 1,000\) | 8.58 | 0.13 | 1.10 |
| De 45 a 49 años | 1,029 | 1,550,158 | \(=(\frac{1,029}{1,550,158})* 1,000\) | 0.66 | 0.12 | 0.08 |
A partir del cuadro anterior puede ahora aplicarse la fórmula de la \(TFG\) que ya conocemos,
\[TFG=\sum_iTEF_i \frac{P_{fi}}{P_{(f15-49)}}=45.4\]
Este resultado significa que, en Colombia, por cada mil mujeres en edad procreativa nacen al año 45.4 bebés.
1.2.4 Tasa de fecundidad total
Si se prescinde de las ponderaciones y se suman las diferentes tasas específicas de fecundidad, se obtiene una medida demográfica independiente de la distribución de la población por edades que se conoce con el nombre de tasa de fecundidad total, \(TFT\), de carácter muy diferente a la anterior tasa de fecundidad general.
Recuérdese que la \(TFG\) indica el número de nacimientos que se producen en un año por cada 1,000 mujeres en edad de procrear. La tasa de fecundidad total, al ser un agregado de tasas de fecundidad específicas no ponderadas, no se refiere a toda una población, sino a un representante típico de ésta. En efecto, la \(TFT\) indica el número de hijos que al final de su vida procreativa tendría una mujer que, al pasar por cada franja de edad, tuviera el número de hijos correspondiente al promedio de todas las mujeres ubicadas dentro de dicha franja. Con esta medida ideal se obtiene una imagen del conjunto de las tasas de fecundidad específica de un país, región o estrato y de sus posibles tendencias, haciendo caso omiso de la distribución de la población por edades. Usualmente las \(TEF\) vienen dadas para rangos de edades de cinco años, tales como 15-19, 20-24, etc. Para obtener la \(TFT\) en este caso, cada \(TEF\) debe ser multiplicada por cinco y dividida por 1,000, puesto que las \(TEF\) expresan el número de hijos que cada año tendrán cada mil mujeres en el respectivo rango de edad.
Ejemplo 1.6 - Cálculo de la tasa de fecundidad total
Tomando las tasas de fecundidad específicas del ejemplo anterior, se puede obtener fácilmente las tasas de fecundidad total al multiplicar por cinco la sumatoria de todas y dividir por 1,000. Así, con datos de Colombia en 2021
\[ TFT= \frac{5\times( 53.43+81.96+71.54+51.6+29.24+8.58+0.66 )}{1,000}\]
\[=1.49\]
En este ejemplo, 1.49 sería el número de hijos que al final de su vida procreativa tendría una mujer, que, al pasar por cada franja de edad, tuviera el número de hijos correspondiente al promedio de todas las mujeres ubicadas dentro de dicha franja.
1.2.5 Tasa bruta de reproducción y tasa neta de reproducción
Como acabamos de ver, la tasa de fecundidad total indica el número total de hijos que una mujer tendría al final de su vida procreativa, en caso de ajustarse a los patrones de fecundidad existentes en un momento para cada franja de edades. De ese total de hijos, varones y mujeres, sólo éstas reemplazarán a la madre en la actividad procreativa. Por consiguiente, si se suma el número promedio de hijas por mujer de todas las franjas de edades entre 15 y 49 años, se obtiene un indicador del potencial de fecundidad futura. Este indicador se conoce con el nombre de tasa bruta de reproducción, \(TBR\).
La \(TBR\) mide el número total de hijas que una mujer tendría durante toda su vida procreativa, dadas ciertas condiciones de fecundidad; pero no dice exactamente por cuántas mujeres será remplazada cada mujer al final de su vida procreativa porque no tiene en cuenta su posibilidad de muerte, como sí lo hace la tasa neta de reproducción, \(TNR\). La \(TNR\) es una medida del número de hijas que tendría una cohorte de niñas recién nacidas que afrontara las tasas de mortalidad y de fecundidad específicas para cada rango de edad hasta alcanzar el final de su vida procreativa. Algunas de estas niñas morirán antes de la edad de reproducción, otras durante su vida procreativa y otras vivirán aún más. Una \(TNR\) de uno (1) indica que la población se está reemplazando exactamente a sí misma. Sin embargo, cuando la \(TNR\) llega a ese punto no se alcanza automáticamente una población estacionaria, ya que las mayores tasas de fecundidad del pasado seguramente habrán ocasionado una gran concentración de mujeres en edad reproductiva, de forma que durante muchas décadas los nacimientos seguirán superando las defunciones.
Ejemplo 1.7 – Cálculo de la tasa bruta de reproducción
Suponga que por cada 1000 nacimientos, 497 son mujeres, y que la \(TFT\) es de tres hijos por mujer a lo largo de su vida procreativa. Por tanto la tasa bruta de reproducción es:
\[TBR=3.0\times\frac{497}{1,000}=1.49\]
Es decir que el número de hijas por mujer a lo largo de su vida procreativa es de 1.5 aproximadamente.
1.2.6 Las pirámides de población, la razón de dependencia y la ventana de oportunidad o bono demográfica
Como hemos visto, la composición por edades y sexo de la población tiene una gran incidencia sobre el crecimiento demográfico (aparte de ser resultado de los patrones de crecimiento demográfico del pasado). Además, la distribución de la población por grupos de edad influye sobre muchos fenómenos económicos, tales como la estructura de las necesidades de consumo, los requerimientos de diferentes tipos de gasto social o las posibilidades de ahorro de una comunidad, entre otros.
La composición de la población por edades y sexo puede describirse mediante una serie de porcentajes correspondientes a los diferentes grupos o, como es más usual, mediante pirámides de población, en las cuales se representa gráficamente el tamaño de cada grupo por edad y sexo. En el Gráfico 1.3 se presentan pirámides de población dinámicas entre 1950 y 2100 para Colombia, Nigeria y Japón (este gráfico puede verse de manera interactiva en la versión HTML del libro). Puede observarse que estos países han tenido y tendrán ritmos muy distintos de aumento de su población, resultado de cambios muy diferentes en la composición de la población por edades a través del tiempo. La transición demográfica está más avanzada en Japón que en Colombia, y mucho menos en Nigeria que en Colombia.
Fuente: Banco Mundial
Fuente: Banco Mundial
Fuente: Banco Mundial
Existe, además, un indicador simplificado, denominado razón de dependencia, que relaciona la población en edades económicamente improductivas con el resto de la población. En forma convencional se considera que los individuos menores de 15 años y los mayores de 65 no tienen capacidad de desempeñar actividades productivas1. Por consiguiente, la razón de dependencia (en porcentaje), \(RD\), se define como
\[{\huge{\checkmark}}RD=\frac{P_{<15}+P_{\geq65}}{P_{\geq15-<65}} \times100\]
La razón de dependencia es una medida resumida de la estructura de edades de la población, que sirve como indicador de la carga económica que tienen en promedio quienes están en edad productiva, y que puede reflejar las limitaciones de recursos humanos productivos que afronta una población. Sin embargo, la razón de dependencia no debe tomarse como un indicador de empleo o desempleo, los cuales analizaremos en el capítulo siguiente. Mientras que éstos hacen referencia a qué tanto se utilizan efectivamente las capacidades productivas disponibles de una población, la razón de dependencia compara hipotéticamente las poblaciones con y sin capacidad de tener una actividad productiva, aunque entre los últimos se incluyan quienes no trabajan por cualquier razón.
Ejemplo 1.8 - Razón de dependencia
Para calcular la razón de dependencia de Colombia para el año 2021, se cuenta con la información de la población por grupos de edad:
Población colombiana por grupos de edad (2021)
| Grupos de edad | Población |
|---|---|
| De 0 a 4 años | 3,922,169 |
| De 5 a 9 años | 3,957,795 |
| De 10 a 14 años | 3,973,505 |
| De 15 a 19 años | 4,102,336 |
| De 20 a 24 años | 4,312,904 |
| De 25 a 29 años | 4,288,150 |
| De 30 a 34 años | 3,954,276 |
| De 35 a 39 años | 3,661,744 |
| De 40 a 44 años | 3,320,634 |
| De 45 a 49 años | 2,941,686 |
| De 50 a 54 años | 2,848,466 |
| De 55 a 59 años | 2,657,919 |
| De 60 a 64 años | 2,229,425 |
| De 65 a 69 años | 1,723,800 |
| De 70 a 74 años | 1,257,119 |
| De 75 a 79 años | 847,828 |
| De 80 y más | 1,049,742 |
| 51,049,498 |
Teniendo en cuenta la fórmula, se hacen los siguientes cálculos:
\[P_{<15}= N_{0-4}+\dotsc+N_{10-14}= 11,853,469\]
\[P_{\geq65}=N_{65-69}+\dotsc+N_{80 y más}= 4,878,489\]
\[P_{\geq15-<65}=N_{15-19}+\dotsc+N_{60-64}= 34,317,540\]
\[RD=\frac{P_{<15}+P_{\geq65}}{P_{\geq15-<65}} \times100\]
\[RD=\frac{(11,853,469+4,878,489)}{34,317,540}\times 100 = 48.76\]
En conclusión, según la razón de dependencia, por cada 100 colombianos en edad productiva hay 49 que no están en edad productiva.
Cuando la razón de dependencia es baja, es más fácil para la población productiva hacerse cargo de los grupos de edad que no son productivos. Esto da origen al concepto de ventana de oportunidad demográfica, o bono demográfico, que la Oficina de Población de las Naciones Unidas define como el período durante la transición demográfica en el que la proporción de niños y jóvenes menores de 15 años cae por debajo del 30% y la proporción de personas de 65 años o más está aún por debajo del 15%.
En el Gráfico 1.4 se muestra que en Colombia, la ventana de oportunidad demográfica se extiende entre 2006 y 2034 (este gráfico puede verse de manera interactiva en la versión HTML del libro). De datos semejantes, que provienen de las Naciones Unidas, puede deducirse que en Nigeria la ventana de oportunidad demográfica sólo empezará hacia 2070 y se extenderá más allá del año 2100. En cambio, en Japón ocurrió entre 1961 y 1996.
El Gráfico 1.4 muestra la estructura de la población proyectada para 2014 y 2020 (este gráfico puede verse de manera interactiva en la versión HTML del libro). Puesto que las dos pirámides tienen formas distintas, está implícito que el proceso de transición demográfica aún no había concluido. A medida que avanza la transición, tiende a equilibrarse la estructura entre todos los grupos. En los años proyectados, los grupos de mayor edad ganarán importancia relativa frente a los demás. Es el momento de explicar cómo hacen los demógrafos sus proyecciones demográficas.
Fuente: Naciones Unidas
1.3 Proyecciones demográficas
Los indicadores demográficos descritos en la sección anterior pueden utilizarse para proyectar el tamaño y la composición de la población. Las proyecciones demográficas se basan necesariamente en indicadores conocidos cuyo comportamiento futuro es incierto, y por tanto tienen siempre un carácter hipotético, o sea, basado en supuestos. Sin embargo, la escogencia de los supuestos determina la relevancia de la proyección, dado el conocimiento que se tiene en el momento de las características y tendencias demográficas de una población.
Los demógrafos utilizan dos métodos de proyecciones que difieren en cuanto a sus características y resultados: los métodos de modelos matemáticos y los métodos de componentes. Mediante los primeros, la población se proyecta acudiendo a funciones matemáticas que se ajustan al comportamiento observado y a ciertas teorías sobre el crecimiento de la población. El método matemático más sencillo es el geométrico a partir de una función del tipo:
\[{\huge{\checkmark}}P_t=P_0(1+r)^t \]
donde \(P_t\) es la población proyectada para el período \(t\), \(P_0\) la población inicial en el período 0 y \(r\) la tasa de crecimiento por unidad de tiempo, \(t\). En este método, r se toma como un supuesto y puede ser igual a su valor observado en un período anterior.
Un método matemático similar que tiene en cuenta el crecimiento continuo (a diferencia del anterior que sólo admite un crecimiento periódico), es el basado en una función de crecimiento exponencial continuo del tipo:
\[{\huge{\checkmark}}P_t=P_0 e^{gt} \]
donde \(e\) es la base de los números naturales y \(g\) la tasa de crecimiento continuo o instantáneo, que se toma como un supuesto, al igual que la tasa de crecimiento \(r\), del método geométrico2. De igual forma, pueden utilizarse funciones más complicadas, que supuestamente corresponden a los comportamientos observados o teóricamente esperados de crecimiento de la población.
Ejemplo 1.9 – Proyecciones de población
Suponga que el 31 de diciembre de 2019 la población de Colombia fue de 49,395,678 personas. Suponga también que la tasa de crecimiento de la población es de 1.8% anual. Usando el método geométrico la población el mismo día de 2025 sería igual a:
\[P_t=49,395,678\times(1+0.018)^6=54,976,314\]
Y usando el método exponencial
\[P_t=49,395,678\times e^{(0.018\times6)} = 55,029,144\]
Cómo se puede observar la tasa de crecimiento exponencial estima un número mayor de personas. Esto se debe a que en el método geométrico, la población aumenta por adición de una cantidad constante mientras que en el método exponencial, la población aumenta por multiplicación de una cantidad constante llamada razón.
Los métodos de modelos matemáticos poseen la virtud de ser sencillos, pero tienen la desventaja de tomar como un supuesto el patrón de comportamiento agregado de la población, en vez de deducirlo del comportamiento de los diferentes grupos de edad y sexo de la población. Por la misma razón, no permiten detectar los cambios de composición de la población ni el origen de tales cambios. De ahí la difusión y utilidad del método alternativo de proyección por componentes. En esencia, en este método se toma independientemente cada grupo de población por edad y sexo y se le aplican las correspondientes tasas específicas de mortalidad, fecundidad y migración a las que se ajustará su comportamiento futuro, a fin de deducir el número de sobrevivientes, nacimientos y adiciones o sustracciones netas por migración y establecer así su tamaño en el período proyectado.
Si la población existente se encuentra clasificada por sexos y grupos de edad, el número de sobrevivientes dentro de una cierta cantidad de años en cada uno de estos componentes puede calcularse a partir de sus correspondientes tasas específicas de mortalidad, \(TEM\). Si las franjas de edades en que se encuentra clasificada la población son de cinco años (como en el Gráfico 1.3), al cabo de los cinco años a partir del período base todas estas franjas se desplazarán hacia el nivel siguiente. La suma de todos estos sobrevivientes a los cinco años, adicionada a las migraciones netas en cada grupo de edad y sexo, constituirá la población mayor de cinco años en el quinto año de la proyección. La franja siguiente, la de los menores de cinco años en el quinto año, estará constituida por los niños sobrevivientes de los nacimientos que se produzcan en ese lapso más las migraciones netas en ese rango de edad. Para determinar dichos nacimientos puede acudirse a la información sobre el número y distribución de las mujeres en edad de procrear y sobre sus patrones de fecundidad, mortalidad y migración, expresados en las correspondientes tasas específicas de fecundidad, mortalidad y migración neta. Dichos datos permiten determinar los nacimientos en cada uno de los cinco años de la proyección. Sin embargo, no todas las personas que nacen en ese período sobrevivirán en el año 5, pues deberán enfrentar el riesgo de la mortalidad. En consecuencia, cada una de las cohortes de niños nacidos cada año deberá, además, ajustarse según sus respectivas tasas específicas de mortalidad, hasta alcanzar el quinto año de la proyección. De esta manera pueden obtenerse el total de población y sus componentes según edad y sexo en el año 5 y pueden también efectuarse proyecciones sucesivas para períodos mayores.
En los métodos más sencillos de proyección por componentes se toma como información exógena las tasas específicas de fecundidad \(TEF\), de mortalidad \(TEM\), y las tasas específicas de migración neta, \(TEMN\), por edades y sexo y se parte de información censal de cada uno de los grupos de edad y sexo. La tasa de crecimiento de la población o de sus componentes y la distribución de la población por edades en el futuro no son tomadas como datos sino que, por el contrario, aparecen como resultado de la proyección obtenida a partir de las tasas de fecundidad y de mortalidad específicas supuestas. Dichas tasas específicas pueden suponerse iguales a las existentes al hacer la proyección, caso en el cual se parte de la hipótesis de que prevalecerán los patrones de comportamiento demográfico por edades. Sin embargo, las proyecciones pueden suponer cambios futuros en las tasas específicas de fecundidad y mortalidad, según el criterio del investigador y teniendo en cuenta su desenvolvimiento pasado, la experiencia en otros lugares, las actitudes observadas entre las personas, etcétera.
Por último, se debe señalar que los métodos de proyección matemática no son incompatibles con los métodos por componentes. En efecto, ambos pueden combinarse para facilitar la elaboración de una proyección. Esto se lleva a cabo cuando se desea mover la fecha de base de la población inicial de una proyección (por ejemplo, centrar a mitad de año los datos de un censo efectuado en otra fecha del mismo año), o cuando se quiere calcular la población en un momento diferente al que se utilizó para la proyección (por ejemplo, al final de un año, cuando la proyección tomó como fecha de referencia la mitad del año). En estos casos, una simple interpolación mediante una función lineal o exponencial puede ser de gran utilidad para una proyección por componentes.
1.3.1 Censos de población
Los censos son una herramienta estadística esencial porque permiten hacer inventarios exhaustivos de recursos. Los censos de población son particularmente importantes porque registran, de manera universal y en un momento exacto del tiempo, las características demográficas, sociales, y económicas de todos los miembros de la población. En Colombia el organismo encargado del desarrollo y coordinación técnica del censo de población es el DANE.
El primer censo de población en Colombia se llevó a cabo en 1905. A partir de 1951, conjuntamente con los censos de población se han realizado censos de vivienda. Se han hecho censos de población y vivienda en 1951, 1964, 1973, 1985, 2005 y 2018. Aunque los censos han investigado variables laborales, no lo han hecho con los mismos criterios de otras fuentes más frecuentes de información, como son las encuestas de hogares (véase el Capítulo 2.). Algunos censos han recibido fuertes críticas por razones metodológicas. Fue el caso del censo de 1993, por dos razones principales: los mapas cartográficos no estaban suficientemente actualizados y por tanto se debió hacer un ajuste por cobertura del 12%; por otra parte, no se establecieron los controles necesarios para garantizar la calidad de la información y por ende el DANE requirió de dos años adicionales de labores para producir datos definitivos. El censo poblacional de 2005 enfrentó menos problemas metodológicos, gracias a que hizo uso de importantes innovaciones técnicas, como el computador de mano (Dispositivo Móvil de Captura, DMC) sobre el cual se cargó el formulario electrónico. El censo más reciente fue el de 2018, cuyos resultados completos se publicaron en 2019. El censo indagó sobre características de la población como sexo, edad, pertenencia étnica, nivel cultural, situación económica; y sus respectivas condiciones de vida, como la conformación de los hogares, jefatura de hogar, tipos de vivienda, y el acceso a servicios públicos. La información recopilada se presenta en tres módulos:
¿Cuántos somos?: Presenta la distribución de la población por sexo, grupos de edad (estructura de la población) y el porcentaje de personas (proporción) que tienen dificultades para realizar actividades cotidianas, así como las que saben leer y escribir, las que asisten a alguna institución educativa en los departamentos y municipios de la región, nivel educativo alcanzado, fecundidad por grupos de edad, promedio de hijos por mujer. También se presenta información de migración interdepartamental en el último año, características de los extranjeros residentes en Colombia (sexo, edad, ocupación, nivel educativo), inmigración internacional en los últimos 5 años y el último año.
¿Dónde estamos?: Presenta la distribución por ubicación geográfica de la población, los hogares y las viviendas en el territorio nacional (cabeceras municipales, rural disperso, centros poblados), así como el lugar de nacimiento de los residentes en los departamentos y municipios de la región. También se presentan los indicadores demográficos por departamento, la tasa de alfabetismo por departamento, el porcentaje (proporción) de migración interna por departamento.
¿Cómo vivimos?: Presenta el total de hogares y viviendas, su uso (residencial o mixto), su distribución por tipo (casa, apartamento, cuarto, étnica), el acceso a servicios públicos, de dónde obtienen el agua los hogares para preparar los alimentos; además, el porcentaje de personas (proporción) por hogar en los departamentos y municipios de la región, los tipos de hogar (unipersonal, nuclear, monoparental, extensos), y porcentaje de mujeres y hombres que son jefes de hogar.
Conceptos clave
| Conceptos demográficos |
| Tasa de crecimiento de la población, \(\textit{TCP}\) |
| Tasa de crecimiento vegetativo, \(\textit{TCV}\) |
| Tasa bruta de natalidad, \(\textit{TBN}\) |
| Tasa bruta de mortalidad, \(\textit{TBM}\) |
| Tasa neta de migración, \(\textit{TNM}\) |
| Transición demográfica |
| Tasas específicas de mortalidad, \(\textit{TEM}\) |
| Esperanza o expectativa de vida |
| Tasa específica de fecundidad, \(\textit{TEF}\) |
| Tasa de fecundidad general, \(\textit{TFG}\) |
| Tasa de fecundidad total, \(\textit{TFT}\) |
| Tasa bruta de reproducción, \(\textit{TBR}\) |
| Tasa neta de reproducción, \(\textit{TNR}\) |
| Pirámide de población |
| Razón de dependencia |
| Ventana de oportunidad demográfica |
| Proyecciones demográficas |
| Modelos matemáticos |
|
|
| Métodos de componentes |
Preguntas y ejercicios
Pregunta 1.1
¿A qué se deben los cambios en la tasa bruta de mortalidad cuando han permanecido inalteradas las tasas específicas de mortalidad?
Pregunta 1.2
A partir de los datos del siguiente cuadro calcule la tasa bruta de mortalidad en Colombia en 2021
| Grupo | Hombres (1) | Mujeres (2) | \(TEM_{Hombres} (3)\) | \(TEM_{Mujeres} (4)\) | \(TEF_i\) (5) |
|---|---|---|---|---|---|
| De 0 a 4 años | 2,003,850 | 1,918,319 | 2.12 | 2.04 | NA |
| De 5 a 9 años | 2,021,769 | 1,936,026 | 0.22 | 0.20 | NA |
| De 10 a 14 años | 2,028,355 | 1,945,150 | 0.32 | 0.30 | NA |
| De 15 a 19 años | 2,085,935 | 2,016,401 | 0.92 | 0.88 | 53.43 |
| De 20 a 24 años | 2,173,233 | 2,139,671 | 1.56 | 1.54 | 81.96 |
| De 25 a 29 años | 2,135,292 | 2,152,858 | 1.75 | 1.76 | 71.54 |
| De 30 a 34 años | 1,946,294 | 2,007,982 | 1.90 | 1.96 | 51.60 |
| De 35 a 39 años | 1,782,290 | 1,879,454 | 2.29 | 2.42 | 29.24 |
| De 40 a 44 años | 1,594,976 | 1,725,658 | 3.01 | 3.26 | 8.58 |
| De 45 a 49 años | 1,391,528 | 1,550,158 | 3.90 | 4.34 | 0.66 |
| De 50 a 54 años | 1,330,374 | 1,518,092 | 5.47 | 6.24 | NA |
| De 55 a 59 años | 1,228,721 | 1,429,198 | 8.09 | 9.40 | NA |
| De 60 a 64 años | 1,021,639 | 1,207,786 | 12.45 | 14.72 | NA |
| De 65 a 69 años | 783,132 | 940,668 | 18.14 | 21.78 | NA |
| De 70 a 74 años | 564,288 | 692,831 | 27.35 | 33.58 | NA |
| De 75 a 79 años | 374,091 | 473,737 | 40.80 | 51.67 | NA |
| De 80 y más | 446,464 | 603,278 | 95.94 | 129.65 | NA |
Pregunta 1.3
Con base en una cohorte de 1,000 hombres de 50 años de edad y las TEM del cuadro anterior, calcule su expectativa de vida restante (suponga que quienes llegan a los 95 años de edad mueren en promedio a los 97.5 años de vida).
Pregunta 1.4
¿Corresponde la expectativa de vida al nacer a la edad promedio de las defunciones de una población en un momento dado?
Pregunta 1.5
¿Existe expectativa de vida para las personas que superan la edad promedio de una población?
Pregunta 1.6
¿Es correcto afirmar que si la expectativa de quienes tienen hoy 20 años es vivir otros 50 años, dentro de 10 años será vivir los 40 restantes?
Pregunta 1.7
Utilizando la información del ejercicio 1.2 calcule ahora la tasa bruta de natalidad, la tasa de fecundidad general y la tasa de fecundidad total.
Pregunta 1.8
Suponiendo que por cada 1,000 nacimientos 497 son mujeres, calcule ahora la tasa bruta de reproducción.
Pregunta 1.9
Con base en una cohorte de 1,000 mujeres recién nacidas y las tasas específicas de mortalidad hasta que lleguen a la edad de 50 años, calcule la tasa neta de reproducción.
Pregunta 1.10
Calcule la población masculina entre 40 y 44 años 10 años más adelante (suponga que no hay movimientos migratorios).
Pregunta 1.11
Calcule la población masculina entre 0 y 4 años tres años más adelante (suponga que no hay mortalidad entre mujeres en edad procreativa pero sí entre los recién nacidos cada año, y que de cada 1,000 nacimientos 503 son varones). ¿Qué crítica le haría usted a este método de proyección? (aparte de estos supuestos mencionados).
Pregunta 1.12
Resuelva nuevamente el ejercicio anterior teniendo en cuenta la mortalidad entre las mujeres.
Pregunta 1.13
Utilice la respuesta del punto anterior para calcular la población masculina entre 5 y 9 años varios años más adelante.
Pregunta 1.14
Calcule la tasa de crecimiento geométrico y la tasa de crecimiento exponencial de la población con base en estos datos y explique por qué no son iguales:
Población total en 2020: 50,000,000
Población total en 2030: 60,000,000
Pregunta 1.15
¿Por qué razones pueden ser preferibles los métodos de proyección por componente a los métodos matemáticos?
Soluciones a ejercicios
Las respuestas a todos los ejercicios se pueden ver en los archivos Excel disponibles en el portal del libro.
Respuesta 1.1
A cambios en la distribución de la población por edades.
Respuesta 1.2
La sumatoria del producto de las columnas (1) y (3) más la sumatoria del producto de las columnas (2) y (4) dividido por el total de la población de ambos sexos (puesto que las TEM están expresadas por cada mil personas, la TBM se refiere también a muertes por cada mil personas de la población total):
\[TBM=\frac{150,068,194 + 221,711,895}{24,912,231 + 26,137,267}= 7.28\]
Respuesta 1.4
No. El promedio de defunciones es afectado por la distribución por edades; no así la expectativa de vida.
Respuesta 1.7
La TBN se obtiene por la sumatoria del producto de las columnas (2) y (5) dividido por el total de la población de ambos sexos:
\[TBN=\frac{611,529}{24,940+26,137}=11.97\]
- Los datos están dados en miles.
La TFG compara los mismos nacimientos en un año con el total de mujeres entre los 15 y los 49 años (por mil).
\[TFG=\frac{611,529}{2,016+2,140+2,153+2,008+1,879+1,726+1,550}=45.39\]
La TFT es la sumatoria de las TEF multiplicadas por 5 (puesto que cada una es válida para un rango de 5 años de edad) y dividida por mil (porque se refiere a cada mujer).
\[TFT=\frac{5\times297 }{1,000}=1.49\]
Respuesta 1.8
La misma TFT ajustada por la proporción de nacimientos de mujeres en el total
\[TBR=\frac{1.49\times497 }{1,000}=0.74\]
Respuesta 1.10
| Rango de edad (1) | Población en 2021 (hombres) (2) | TEM por mil(3) | Tasa de sobrevivencia anual (4) | Tasa de sobrevivencia en 4 años (4) = (1-TEM)^4 | Sobrevivientes en 2025 (5) = (2) * (4) del renglón anterior | Sobrevivientes en 2029 (6) = (5)*(4) del renglón anterior |
|---|---|---|---|---|---|---|
| … | … | … | … | … | … | … |
| 30-34 | 1,946 | 1.9 | 0.998 | 0.992 | … | … |
| 35-39 | … | 2.29 | 0.998 | 0.991 | 1,939 | … |
| 40-45 | … | … | … | … | … | 1,930 |
En este ejemplo sólo se han copiado los datos necesarios para proyectar un componente de la población, pero puede utilizarse el mismo formato para los demás grupos de edad nacidos hasta 2021. Con el objeto de proyectar los nacimientos a partir de 2021 véase el problema siguiente.
Respuesta 1.14
La tasa de crecimiento geométrico se calcula despejando r en la siguiente ecuación:
\[60,000,000=50,000,000(1+r)^{14}\]
\[\left ( \frac{50,000,000}{60,000,000}\right )^{\frac{1}{14}}-1 = -1.29\%\]
La tasa de crecimiento exponencial se obtiene encontrando g en
\[60,000,000=50,000,000e^{14g}\]
donde e constituye la base de los números naturales.
Tomando logaritmos naturales (base e)
\[Ln(60,000,000)=Ln(50,000,000)+14g\]
\[g = 1.30\%\]
Bibliografía
Libros de texto y estudios destacados
Banco Interamericano de Desarrollo, Desarrollo más allá de la economía. Informe de Progreso Económico y Social, 2000. Washington, D.C. El Capítulo 2 analiza la evolución y perspectivas demográficas de América Latina y discute los principales canales de influencia de la demografía en el desarrollo. Puede consultarse en línea en: http://www.iadb.org/es/investigacion-y-datos/detalles-de-publicacion,3169.html?pub_id=b-2000.
Flórez N., Carmen Elisa, “Las transformaciones sociodemográficas en Colombia durante el siglo XX”. Banco de la República-TM Editores, 2000. Un excelente trabajo descriptivo, en el cual se ofrece una visión integrada de los cambios demográficos, laborales y sociales a lo largo del siglo XX.
Urdinola C., B. Piedad, “Demografía colombiana: En preparación para la era del envejecimiento”, en Fedesarrollo, Descifrar el futuro: La economía Colombiana en los próximos diez años, Debate, Penguin Random House Grupo Editorial, 2021.
Preston, Samuel H., Patrick Heuveline y Michel Guillot, Demography. Measuring and Modeling Population Processes. Blackwell Publishers, 2001. Muy didáctico, es uno de los textos de introducción a los métodos de medición demográfica más utilizados actualmente.
Shryock, Henry y Siegel, Jacob S. and Associates, The Methods and Materials of Demography, condensed edition by Edward G. Stockwell, Academic Press, 1976. Texto clásico de demografía; detallado y técnico.
Fuentes de información estadística periódica
DANE. Es la fuente oficial de las estadísticas demográficas en Colombia. La información en línea se encuentra en: http://www.dane.gov.co/index.php/estadisticas-por-tema/demografia-y-poblacion
Naciones Unidas. http://unstats.un.org/unsd/demographic/default.htm Contiene estadísticas históricas y proyecciones demográficas por períodos quinquenales para todos los países del mundo.