2 Partes de una visualización en ggplot2

En el Capítulo 1 vimos varios ejemplos de visualizaciones realizadas con el paquete ggplot2. Afirmamos que, a diferencia de las funciones gráficas propias de la base de R, ggplot2 es más intuitivo y sigue una gramática (lógica) de los gráficos. En este Capítulo discutiremos esa gramática entendiendo cada uno de los componentes de un gráfico, como por ejemplo el que se presenta en la Figura 2.1.

Figura 2.1: Relación entre el PIB percápita y la expericencia de vida al nacer por país (2007)

Fuente: Datos del paquete gapminder.

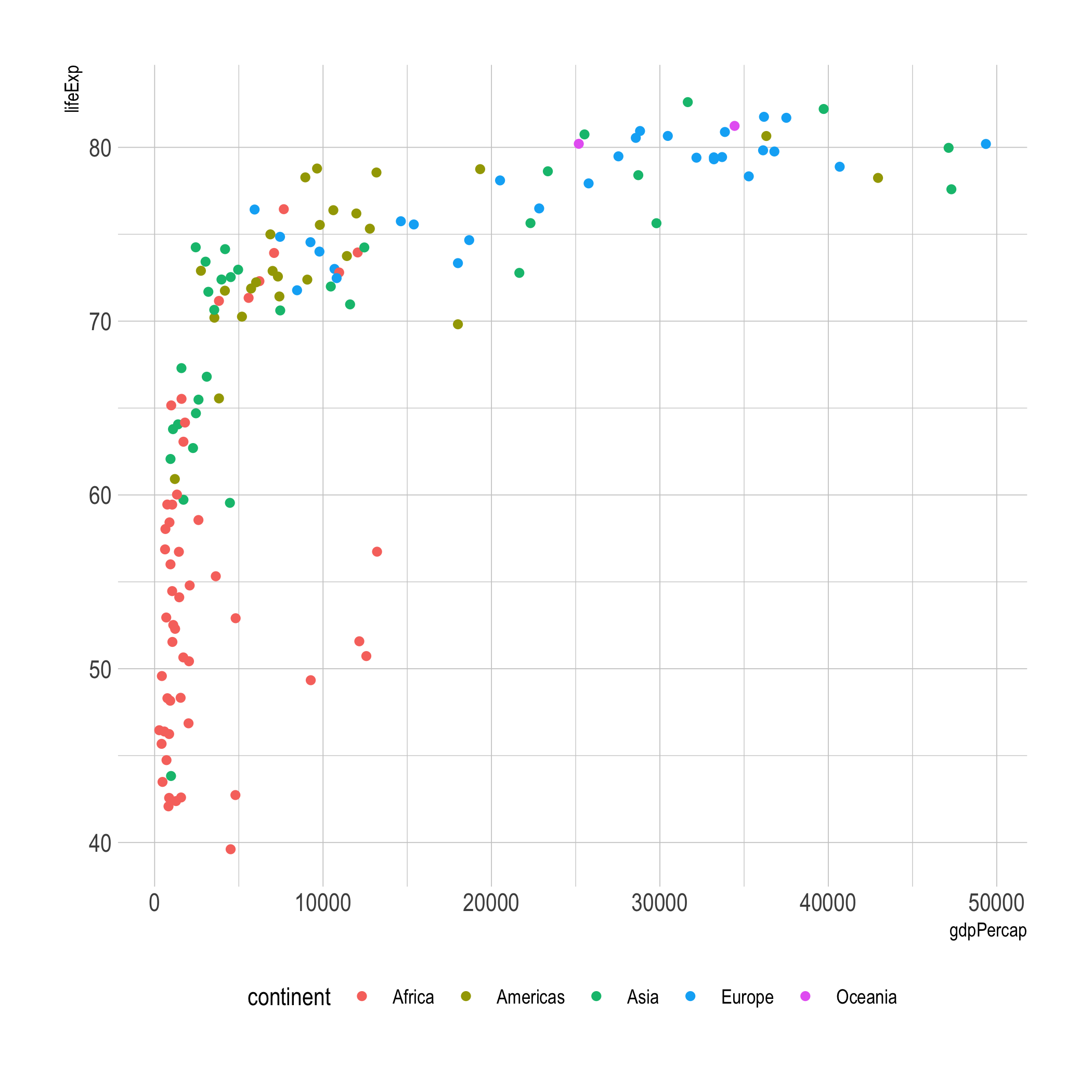
La Figura 2.1 parte de unos datos (que salieron del paquete gapminder (Bryan, 2017)) y unas decisiones de cómo visualizar esos datos. Reflexionemos un poco sobre todas las decisiones que se tomaron antes de construir el gráfico. Después de tener los datos, se parte de una idea de qué variables “mapear” (graficar) en cada uno de los ejes. En este caso, el PIB percápita (gdpPercap) y la esperanza de vida al nacer (lifeExp). Se eligió cómo representar cada observación (en este caso con puntos) y cómo el color de estos puntos tendría una variable “mapeada”. Se asignó el continente (continent) al color. También, se decidió de manera implícita que el tamaño del punto no tendría ningún significado. Adicionalmente, se seleccionó en qué unidades medir los ejes (las coordenadas). Finalmente, se decidió cómo sería el diseño del gráfico, al escoger la posición de los nombres de las variables en los ejes y si el cuerpo del gráfico tendría grilla¹² y el color del fondo.

En este capítulo discutiremos cada uno de esos componentes y veremos la jerga que se emplea en el paquete ggplot2 para referirse a ellos.

2.1 Componentes

Veamos formalmente cómo ggplot2 emplea la gramática de los gráficos de Wilkinson (2012). Es decir, veamos cuáles son los componentes y cómo estos se sobreponen para obtener un gráfico. En este contexto, un gráfico está compuesto por diferentes capas que se sobreponen de tal manera que el resultado final es una visualización. En la Figura 2.2 se presentan las diferentes capas que componen un objeto de clase ggplot.

Figura 2.2: Capas de una visualización construída con ggplot2

Fuente: Elaboración propia a partir de Wickham (2016) y Eilkinson (2012).

No todas las capas son necesarias para construir una visualización en ggplot2, pero cada una aportará al producto final un elemento diferente. Veamos cada uno de estas capas (layers en inglés):

Datos o data: es la primera capa necesaria para realizar visualizaciones (ver Figura 2.2). Es la base fundamental para construir la visualización y por tanto es una parte obligatoria en la construcción de una visualización en este paquete. Esta capa llama a los datos, que deben estar en un objeto de clase data.frame¹³ o tibble¹⁴. En la Figura 2.1 esta capa corresponde al objeto gapminder (data = gapminder).
Aesthetics: en esta capa se indican las variables que se van a “mapear” (graficar) en los diferntes elementos del gráfico, como ejemplo los ejes, el color y el tamaño de los puntos. Una traducción literal de esta capa sería “estética”, pero de pronto no es una buena traducción. Esta capa indica qué variables del data.frame se mapean a el eje horizontal (denotado por x) y cuál al eje vertical (y). También podemos mapear en esta capa el color (col), como en la Figura 2.1 donde el continente (que es una variable cualitativa) se mapeó al color de cada punto (col = continent). En dicha figura, la variable cuantitativa PIB percápita se representa en el eje horizontal (x = gdpPercap) y la esperanza de vida al nacer (variable cuantitativa) en el eje vertical (y = lifeExp). Adicionalmente, podemos mapear variables (si tiene sentido) al tamaño (size) y otros elementos como la forma del punto. Al igual que la primera capa, esta es obligatoria; constituyéndose, con la capa de los datos, en uno de los tres pilares de cualquier visualización que armemos con ggplot2. Esta capa es conocida en el paquete como aes.
Geometría: esta capa le indica a R qué tipo de visualización se desea obtener. Es decir, cuál es la geometría que se desea adoptar para mostrar los datos. Por ejemplo, la geometría podría ser emplear barras, líneas, puntos, histogramas, entre otros. En el caso particular de la Figura 2.1 la geometría seleccionada fue los puntos (geom_point). Hay distintas opciones que se explorarán más adelante en los Capítulos 3, 4 y 5. Esta capa es obligatoria y constituye el tercer pilar indispensable en toda visualización de ggplot2.
Facets: esta capa permite descomponer un gráfico en sub-gráficos (cuadrículas o facetas) según una variable cualitativa. Por ejemplo, en vez de usar colores para distinguir los continentes, como se hace en la Figura 2.1, podríamos construir 5 sub-gráficos cada uno para un continente como en la Figura 2.6. Las facetas sirven para comparar grupos, separándolos y así facilitando la identificación de los grupos. No es una capa obligatoria.
Estadísticas: esta capa permite adicionar información estadística que permita resumir los datos. Por ejemplo, se puede adicionar una línea de tendencia para los datos. No es obligatoria.
Escalas: esta capa permite indicar en qué escala se presentan los datos en cada uno de los ejes. Por ejemplo, en algunas ocasiones se podría desear presentar uno de los dos ejes en escala logarítmica. No es obligatoria.
Coordenadas: esta capa determina cómo se combinan las variables seleccionas para los ejes x (horizontal) y y (vertical) en la capa de estética. En últimas esta capa define el espacio en el que se mapearán los datos. Por ejemplo, en algunas ocasiones será útil poner límites a los ejes, intercambiar lo que se presenta en un eje con el otro, o asegurarnos que los dos ejes tienen la misma magnitud.
Tema: es la capa destinada a la apariencia final de la gráfica. Podemos encontrar unos temas predeterminados cargados con el paquete ggplot2 y también se puede crear un tema para que se adapte a la imagen institucional o al tipo de diseño de todo el documento. También existen algunos paquetes que incluyen temas adicionales. Aquí se modifica el color del fondo, ejes, tamaños, grilla, posición de los nombres de los ejes, entre otros. No es obligatoria.

Veamos un ejemplo para entender mejor cada capa y sus argumentos.

2.2 Primeros pasos con ggplot2

Para empezar a trabajar con visualizaciones en R debemos instalar el paquete ggplot2 (Wickham, 2016), en caso de que no esté instalado en el equipo. Los paquetes incluyen diversas funciones, para tareas generales o específicas¹⁵. En especial, este paquete contiene herramientas de visualización. Para proceder a la instalación, puedes emplear la función install.packages().

install.packages("ggplot2")

La instalación de un paquete solo es necesaria una vez. Recuerda que tenemos que pedirle a R que cargue el paquete cada vez que iniciemos una nueva sesión. Para esto, emplea la función library() . Carguemos el paquete ggplot2.

library(ggplot2)

Para nuestro ejemplo usaremos el objeto de datos gapminder del paquete gapminder (Bryan, 2017) que ya empleamos en la Sección 1.2. Carga el objeto gapminder.

# cargar paquete
# install.packages("gapminder")
library(gapminder)
# cargar datos
data("gapminder")

Veamos cómo materializar lo descrito en la sección anterior (Sección 2.1). Veíamos que de las siete capas descritas, las capas de Datos, Aesthetics y Geometría son esenciales. Las dos primeras capas, se especifican empleando la función ggplot() . El primer argumento de esta función corresponde a la primera capa: los datos¹⁶. El argumento data puede ser un objeto de clase data.frame o tibble.

ggplot(data = gapminder)

Figura 2.3: Primera capa (datos) de la Figura de relación entre PIB percápita y Expectativa de vida al nacer por país (1952 - 2007)

Fuente: Datos del paquete gapminder.

Correr solo esta parte de la función tendrá como resultado un gráfico en blanco (ver Figura 2.3), porque aún nos faltan los otros dos pilares necesarios para una visualización: Las capas Aesthetics y Geometría.

La segunda capa, Aesthetics, se especifica como otro argumento de la función ggplot(). La función aes() permite especificar cómo se mapearán las variables a los diferentes elementos de la visualización. Para este primer ejemplo, se quiere mostrar la relación entre dos variables numéricas (o cuantitativas): la expectativa de vida al nacer (lifeExp) y el PIB percápita (gdpPercap). Entonces, se representará en el eje horizontal (x) la variable lifeExp y al eje vertical (y) la variable gdpPerCap, dentro del argumento aes().

Es decir, la primera y segunda capa de la figura corresponderá a la siguiente línea de código:

ggplot(gapminder, aes(x = gdpPercap, y = lifeExp))

Figura 2.4: Primera y segunda capa de la Figura de relación entre PIB percápita y Expectativa de vida al nacer por país (1952 - 2007)

Fuente: Datos del paquete gapminder.

Nota que al correr esta línea, aparece el plano cartesiano en el que se ubicarán los datos, pero no los datos en sí. Esto sucede porque aún nos falta el último pilar: la Geometría (ver Figura 2.4). Es decir, aún no hemos especificado cómo se mapearán los datos. En otras palabras, no se ha especificado el tipo de visualización que vamos a emplear.

La capa de Geometría (geom en la jerga de ggplot2) se especifica mediante una segunda función. Existen diferentes tipos de gráficas como por ejemplo: histogramas, líneas, barras y puntos. Dado que tenemos diferentes posibilidades de geometría, tendremos diferentes funciones para cada una de las posibles geometrías (en los próximos capítulos discutiremos sobre estos temas). Estas funciones se caracterizan por empezar con el prefijo geom_. Por ejemplo, para la visualización que estamos construyendo se desea un diagrama de dispersión en el que cada dato se representa por puntos. Así, la función correspondiente será: geom_point(). Esta capa se suma a las dos capas anteriores de la siguiente manera:

ggplot(gapminder, aes(x = gdpPercap, y = lifeExp))+
  geom_point()

Figura 2.5: Primeras tres capas de la Figura de relación entre PIB percápita y Expectativa de vida al nacer por país (1952 - 2007).

Fuente: Datos del paquete gapminder.

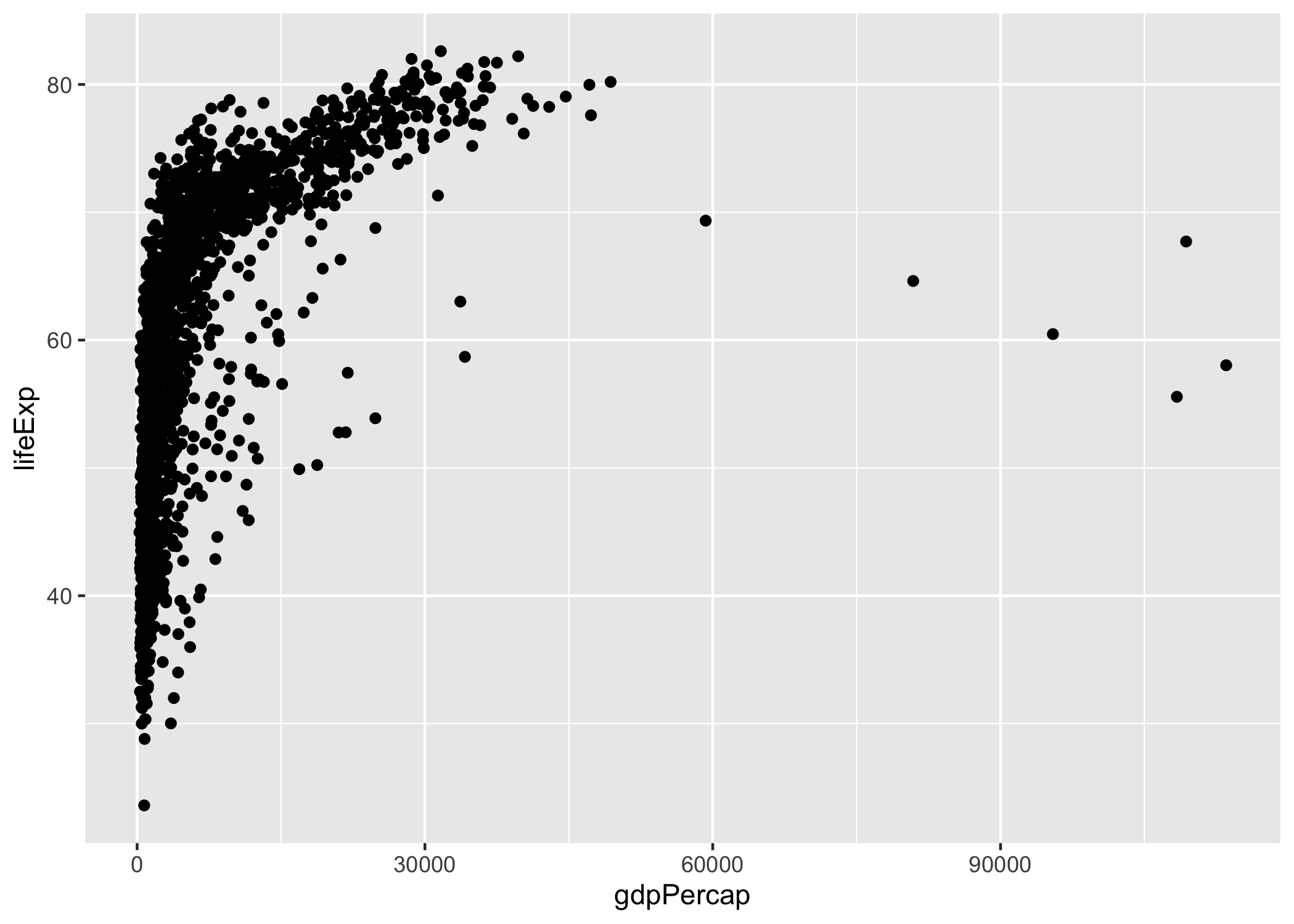
Observa que esta capa se agrega a las dos anteriores con el signo de suma (+). En la Figura 2.5 podemos observar las tres primeras capas esenciales: Datos, Aesthetics y Geometría.

Hasta aquí tenemos las capas necesarias para crear una visualización, pero podemos adicionar otras para mejorarla. Las siguientes capas se pueden agregar, si se desea, en cualquier orden. Por ejemplo, en este caso especial de esta visualización, tendría sentido incluir la capa de Facets.

El objeto gapminder también contiene la variable continente (continent). Si queremos entender la distribución de las dos variables bajo análisis en los diferentes continentes, podemos emplear la capa de Facets para dividir los datos de tal manera que grafiquemos para cada continente la relación entre ellas (ver Figura 2.6).

Esta capa se puede adicionar con la función facet_grid(). Esta función crea una grilla (grid en inglés) o parrilla de gráficos, separando los datos de acuerdo a la variable que se emplee como argumento. Siguiendo la tradición del lenguaje de R, la variable por medio de la cuál se quieran dividir los gráficos debe estar precedida del operador virgulilla¹⁷ (~) . Regresando a la figura que estábamos construyendo, la capa de Facets se puede agregar para que los datos sean visualizados por continente, como se muestra en el siguiente código:

ggplot(gapminder, aes(x = gdpPercap, y = lifeExp))+
  geom_point() +
  facet_grid(~ continent)

Figura 2.6: Primeras tres capas y capa Facets de la Figura de relación entre PIB percápita y Expectativa de vida al nacer por país (1952 - 2007)

Fuente: Datos del paquete gapminder.

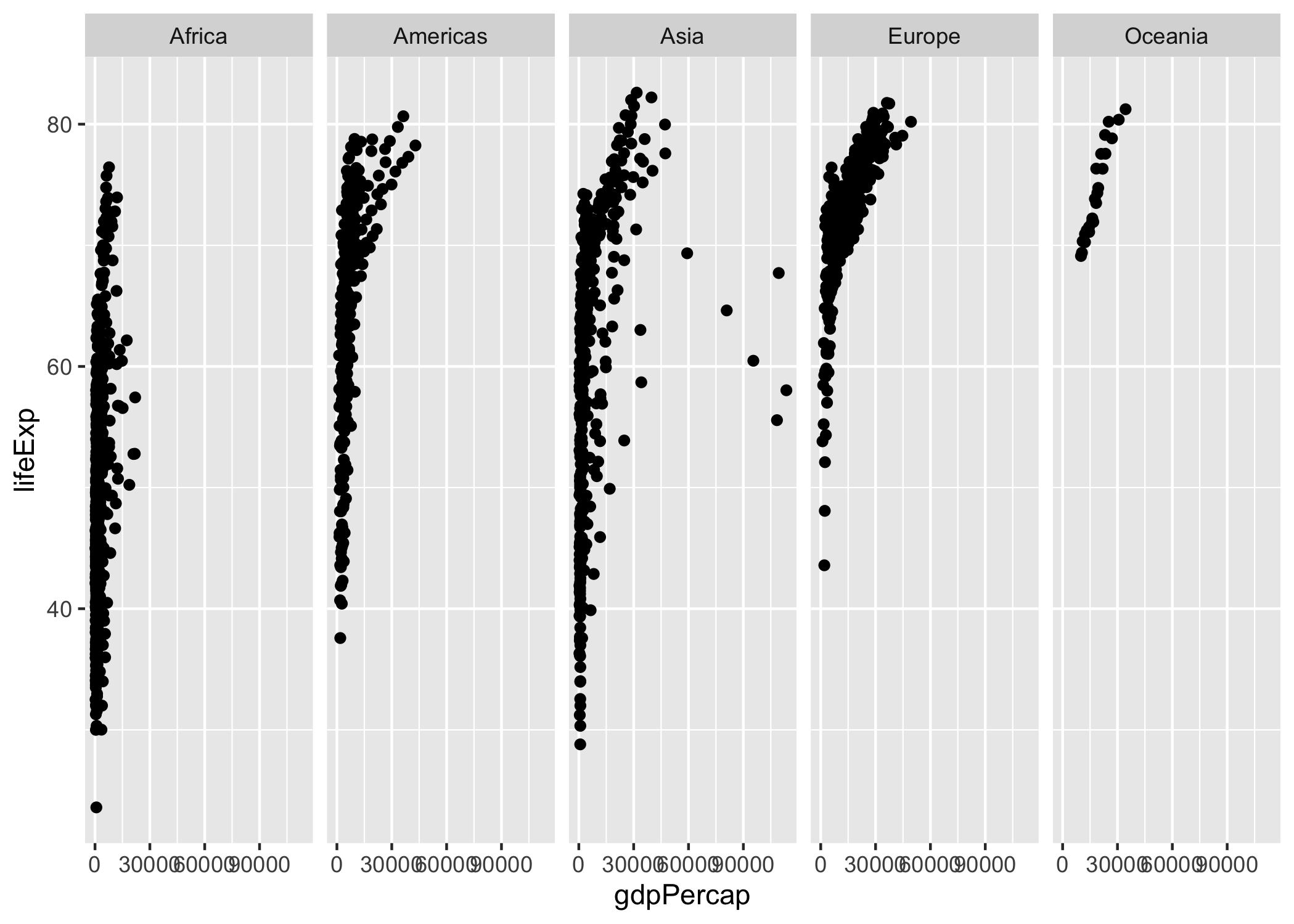
Nota que otra forma de visualizar las diferencias entre continentes podría ser mapear al color la variable continente y no usar la capa de Facets. ¡Inténtalo! El resultado sería algo muy similar a la Figura 2.1. La diferencia es que en la Figura 2.1 se presentan solo datos para el año 2007 y tu gráfica debe tener datos para toda la muestra. En ese caso parece mejor transmitir la idea de las diferencias entre continentes la capa de Facets que mapear los continentes al color del punto. Este tipo de decisiones, sobre qué comunica mejor tu idea siempre estará presente al momento de hacer visualizaciones. Lo mejor será siempre ensayar muchas opciones antes de decidir cuál visualización será la mejor para comunicar tus ideas.

Ahora podemos jugar un poco con la capa de Escalas¹⁸ para ayudarnos a comunicar un mensaje. La capa de Escalas permite cambiar la escala en la que se mide un eje y algunos detalles de cada uno de los ejes como los límites o las etiquetas de cada eje. En otras palabras, esta capa controla los detalles de cómo se traducen los valores de los datos a las propiedades visuales.

Por ejemplo, podríamos cambiar la escala en la que se presentan los datos del PIB percápita (gdpPercap) de dólares por persona a una escala logarítmica (logaritmo base 10) empleando la función scale_x_log10(). Regresando a nuestro ejemplo, cambiemos la escala del eje horizontal para obtener la Figura 2.7 empleando el siguiente código:

ggplot(gapminder, aes(x = gdpPercap, y = lifeExp))+
  geom_point()+
  facet_grid(~continent)+
  scale_x_log10()

Figura 2.7: Capa Facets y Escalas de la Figura de relación entre PIB percápita y Expectativa de vida al nacer por país (1952 - 2007)

Fuente: Datos del paquete gapminder.

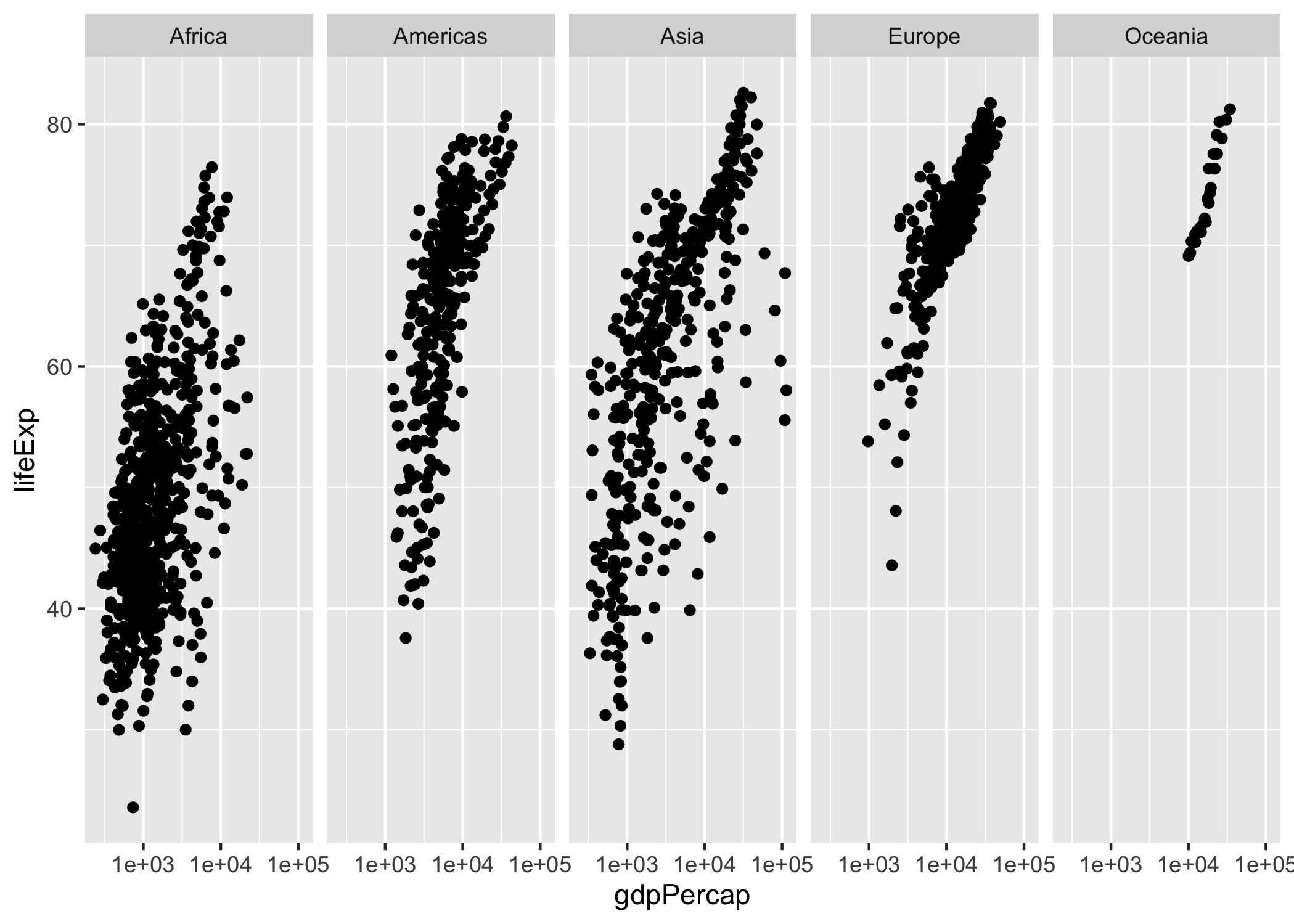
El paquete ggplot2 tiene a disposición diferentes transformaciones y operaciones que podemos hacer con las escalas de los ejes, todas esas funciones empiezan por el prefijo scale_¹⁹.

La capa Escalas también tiene funciones que no empiezan con el prefijo scale_ que modifican elementos de los ejes y los títulos. Por ejemplo, la función labs() permite agregar un título (argumento title), subtítulo (argumento subtitle) y la fuente (argumento caption). También tenemos las funciones xlab() y ylab() que permiten cambiar las leyendas de los ejes que por defecto es el nombre de la variable mapeada. Esta capa también tiene funciones que permiten cambiar los limites de las escalas que se presentan en cada eje (xlim() y ylim()). Tienes que tener cuidado con estas dos últimas funciones, pues cualquier dato fuera de los límites se desechará.

Juega un poco con estas funciones para entender cómo funcionan. Intenta correr el siguiente código y ver el efecto que tiene sobre tu visualización:

ggplot(gapminder, aes(x = gdpPercap, y = lifeExp))+
  geom_point()+
  facet_grid(~continent)+
  scale_x_log10() +
  labs(
  title = "Relación entre  PIB percápita y 
          Expectativa de vida al nacer por país",
  subtitle = "(1952 - 2007)",
  caption = "Fuente: Datos de gapminder") +
  xlab("PIB percápita en logaritmos") +
  ylab("Esperanza de vida al nacer en años")

La capa de Coordenadas es la que le dice a ggplot2 cómo combinar la variable en la capa de Estética mapeada en x y y para construir la visualización en dos dimensiones. Comúnmente estamos acostumbrados a emplear coordenadas cartesianas (el plano cartesiano) para mapear los datos. Por defecto ggplot2 emplea coordenadas cartesianas (función coord_cartesian()²⁰ ). Una función de esta capa que puede ser útil es coord_flip(), que invierte los ejes. Para un ejemplo de la utilidad de esta función puedes ver las Figuras 6.1 y 6.2 del Capítulo 6. Por ahora, intenta el siguiente código:

ggplot(gapminder, aes(x = gdpPercap, y = lifeExp))+
  geom_point()+
  facet_grid(~continent)+
  scale_x_log10() +
  coord_flip()

Otra función útil de esta capa es coord_fixed(), la cual fija la relación entre el espacio que ocupa el eje x y el eje y. Con el argumento ratio podemos establecer el número de unidades en el eje vertical que equivalen a una unidad en el eje horizontal. El valor por defecto es uno (ratio = 1). Una razón mayor a uno, implica que las unidades del eje horizontal serán más largas y viceversa. Por ejemplo, intenta el siguiente código y juega con el argumento ratio:

ggplot(gapminder, aes(x = gdpPercap, y = lifeExp))+
  geom_point()+
  facet_grid(~continent)+
  scale_x_log10() +
  coord_fixed(ratio = 0.05)

La capa de Coordenadas tiene más funciones para hacer mapas (por ejemplo, coord_map(), coord_quickmap() y coord_sf()) y coordenadas polares (coord_polar()). Como con cualquier otra función de este paquete, si necesitas alguna de ellas podrás encontrar una documentación muy completa en línea.

La capa de Estadísticas nos puede servir para reforzar una idea que queremos transmitir con una visualización. Por ejemplo, parece evidente que existe una relación positiva y lineal entre la expectativa de vida al nacer (lifeExp) y el PIB percápita (gdpPercap) (en logaritmos) (ver Figura 2.7). Para mostrar esto visualmente, podríamos incluir una linea de regresión que muestre la relación lineal entre las dos variables. Existen diferentes tipos de estadísticas que nos podrían ayudar a construir nuestra visualización. Estas funciones se caracterizan por empezar con el prefijo stat_. Por ejemplo, la función stat_smooth() ayuda a trazar una linea “suavizada” que se ajuste a los datos. Esta tiene como argumento el método que queremos emplear para trazar la linea de suavización. Por ejemplo si fijamos method = “lm” como método, se está indicando que busque una relación lineal (Lineal Model, por sus siglas en inglés) (ver Figura 2.8).

También podemos modificar el color de la linea de suavización (en este caso la recta de regresión) con el argumento col. Si no se especifica un color, el color será azul por defecto. En nuestro ejemplo tendremos lo siguiente:

ggplot(gapminder, aes(x = gdpPercap, y = lifeExp))+
  geom_point()+
  facet_grid(~continent)+
  scale_x_log10() +
  stat_smooth(method="lm", col="red")

Figura 2.8: Capa Facets, Escalas y Estadísticas de la Figura de relación entre PIB percápita y Expectativa de vida al nacer por país (1952 - 2007)

Fuente: Datos del paquete gapminder.

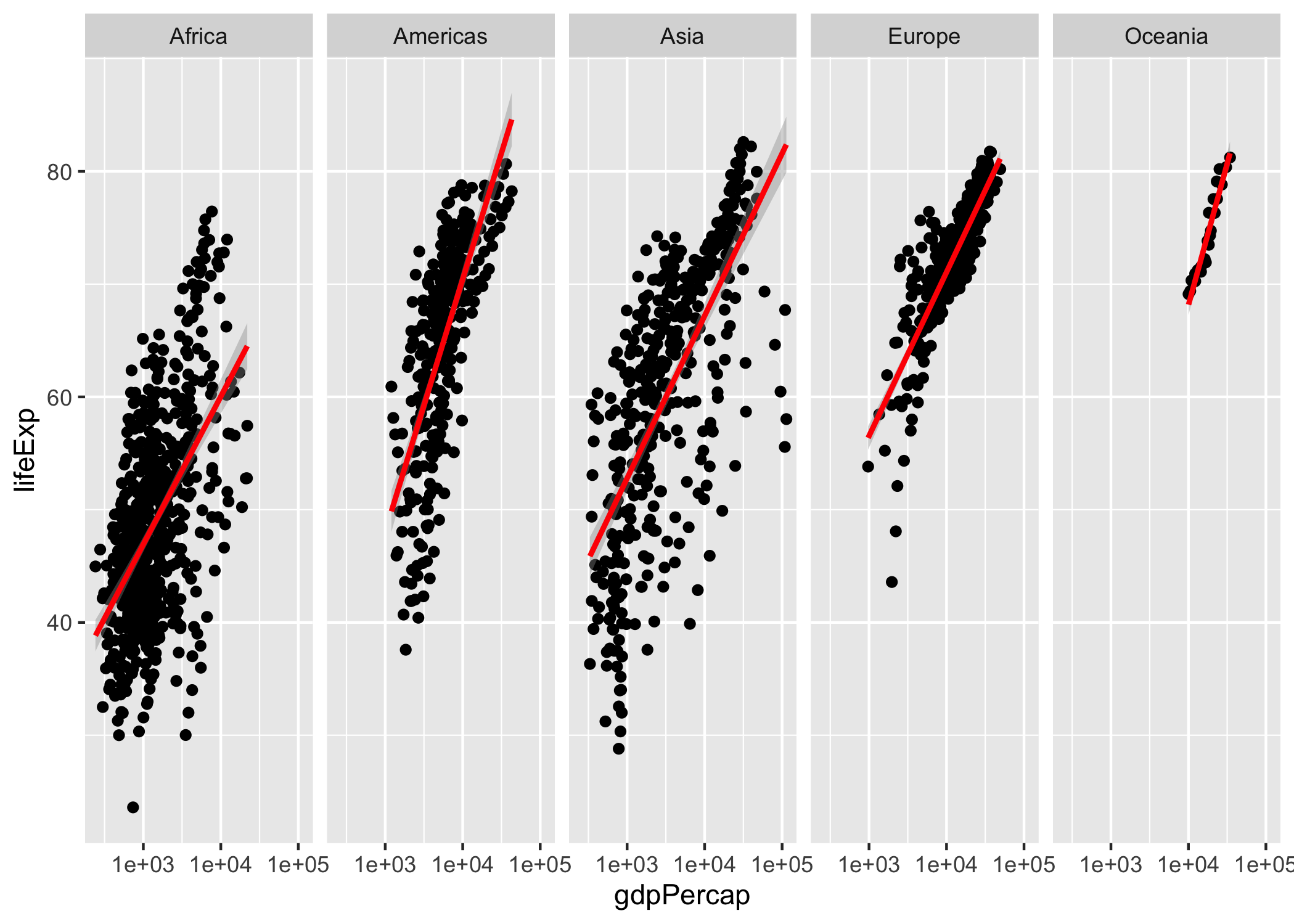
Observa que en la Figura 2.8 se ha trazado una línea de regresión para cada continente empleando todos los datos del respectivo continente²¹ esto transmite mejor la idea de que existe una relación lineal positiva entre el logaritmo del PIB percápita y la esperanza de vida al nacer. Típicamente esta capa se emplea para transmitir algún hallazgo en la exploración o el modelado de los datos.

Nuestra visualización ha cambiado sustancialmente desde la que teníamos en la Figura 2.5. Y podemos continuar modificando nuestra visualización con la capa de Tema. Como se mencionó en la sección 2.1, el paquete ggplot2 viene con temas predeterminados que determinan cómo es el fondo de la figura, la posición y el tamaño de los nombres de los ejes. Pero este paquete también brinda la opción de crear nuevos temas, para poder agregar logos de empresas, tamaños específicos de los elementos, entre otras opciones. En general, el tema ayuda a que la visualización sea estéticamente más acorde al documento donde se va a mostrar (ver Figuras del Capítulo 1).

Dentro de los temas disponibles directamente en este paquete están theme_minimal(), theme_classic(), theme_bw(), entre otros. Siguiendo la misma gramática de las anteriores capas, esta se agrega sumándola a las anteriores. En este caso las funciones de tema (todas inician con el prefijo theme_) no necesitan argumentos para funcionar. Por ejemplo, el siguiente código incorpora el tema minimalista (theme_minimal()) (ver Figura 2.9).

ggplot(gapminder, aes(x = gdpPercap, y = lifeExp))+
  geom_point()+
  facet_grid(~continent)+
  scale_x_log10() +
  stat_smooth(method="lm", col="red") +
    theme_minimal()

Figura 2.9: Figura de relación entre PIB percápita y Expectativa de vida al nacer por país (1952 - 2007) con tema minimalista

Fuente: Datos del paquete gapminder.

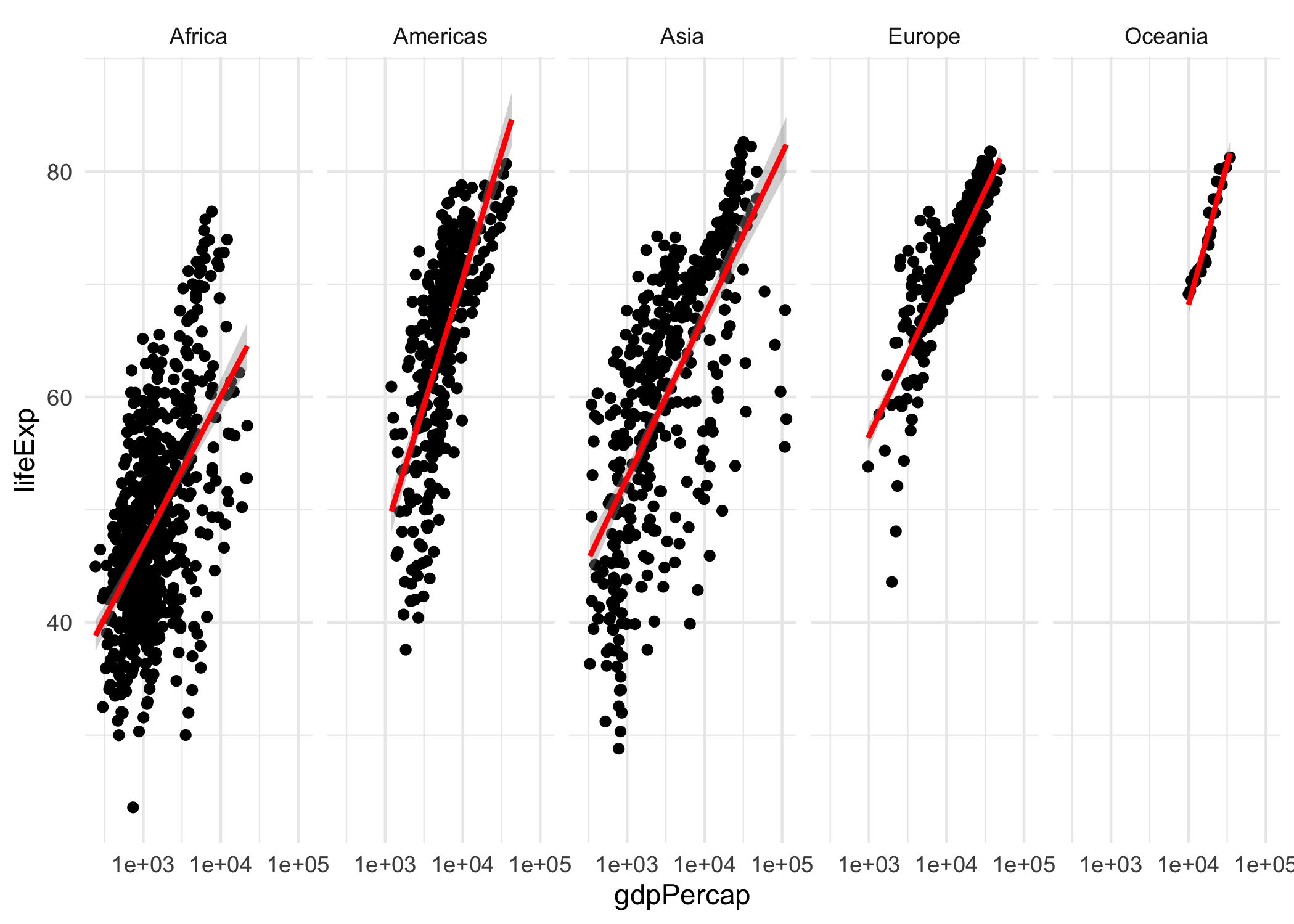
Ahora puedes intentar jugar con las diferentes opciones de temas. Por ejemplo, la Figura 2.10 emplea la función theme_classic(). Con estas ocho capas, el paquete ggplot2 nos brinda una gran flexibilidad para hacer visualizaciones rápidamente.

Figura 2.10: Figura de relación entre PIB percápita y Expectativa de vida al nacer por país (1952 - 2007) Con tema clásico

Fuente: Datos del paquete gapminder.

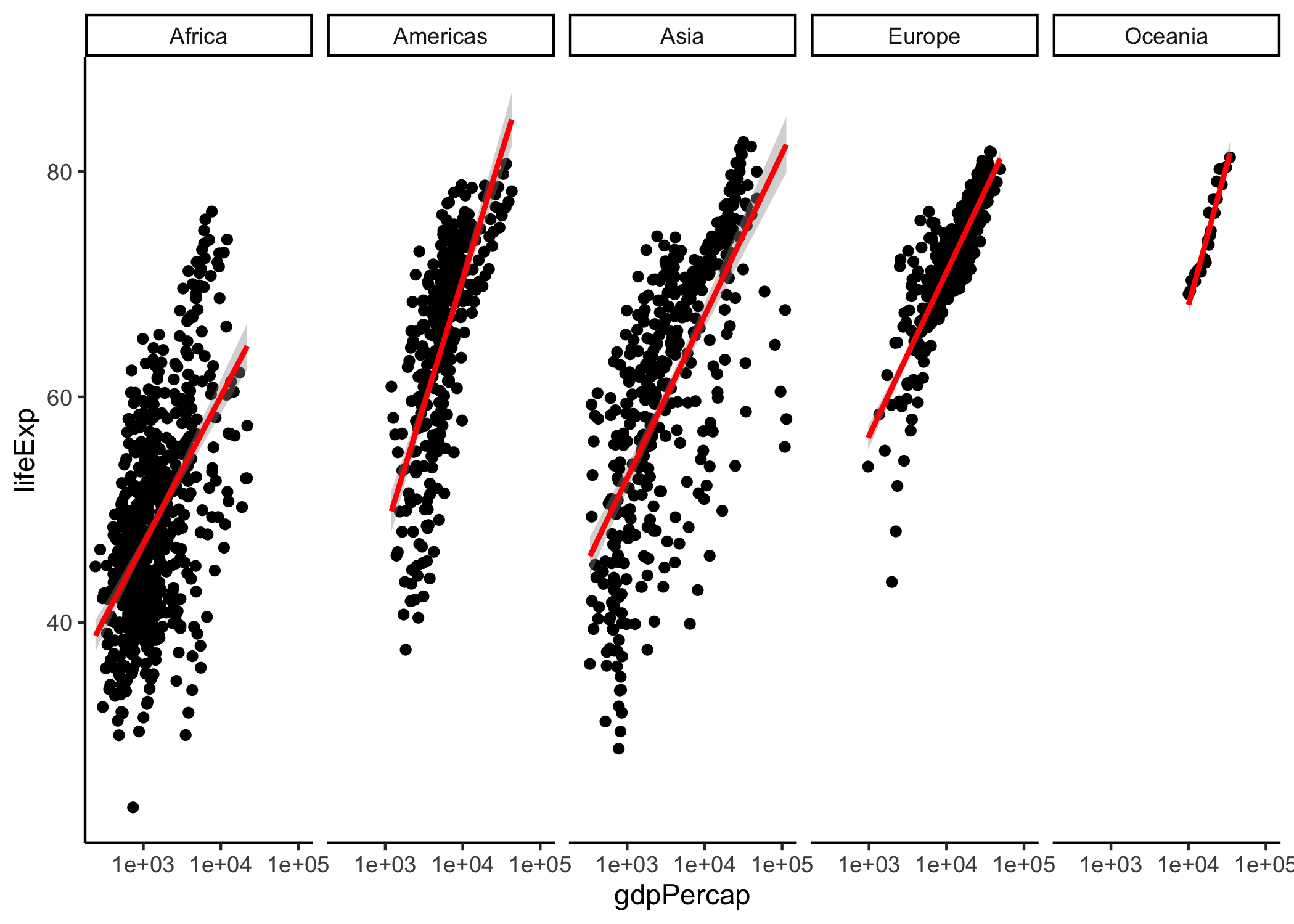
Para resumir, en la Figura 2.11 se resume de manera esquemática cada una de las capas y el correspondiente código empleado para generar la Figura 2.9

Figura 2.11: Capas de la Figura 2.9. y su respectivo código

Fuente: Elaboración propia a partir de Wickham (2016) y Eilkinson (2012).

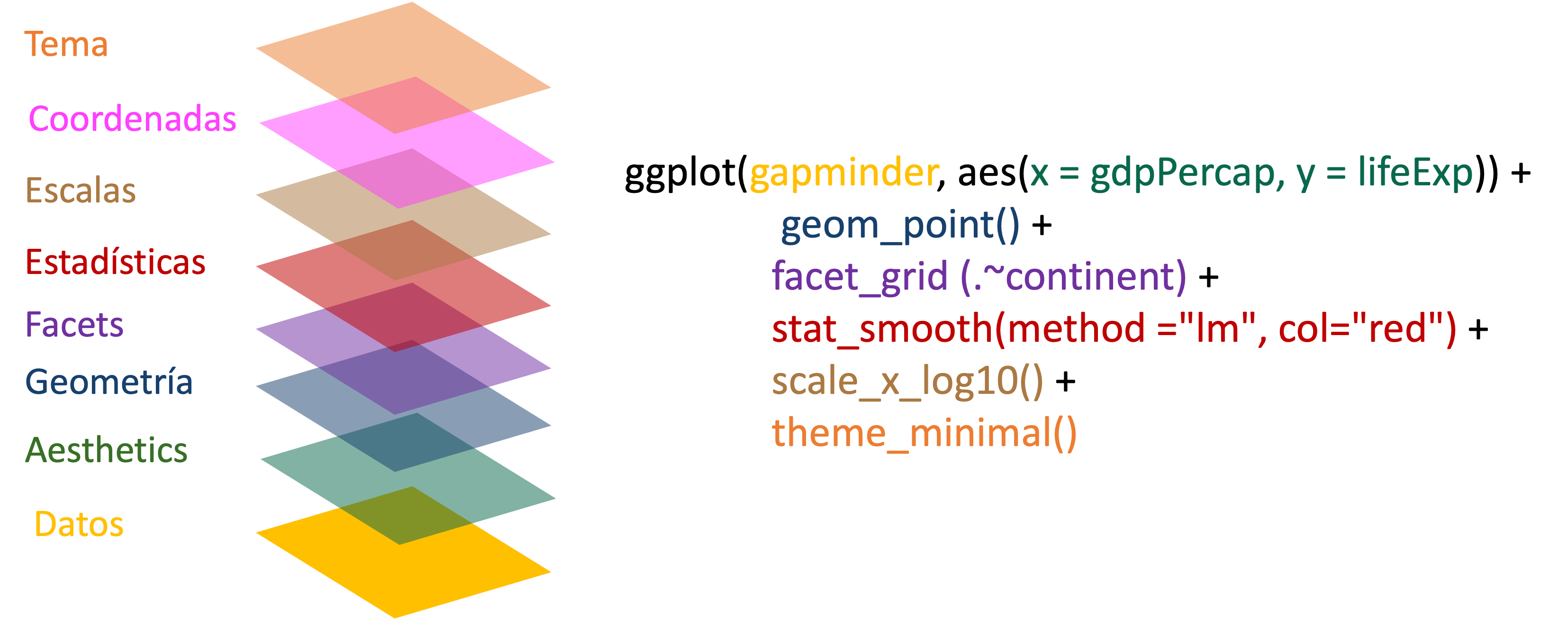
2.3 Comentarios finales

Antes de continuar, es importante mencionar que este paquete y otros adicionales, permiten incluir más capas y funciones de las que vimos en este capítulo. Por ejemplo, se pueden usar funciones de otros paquetes para agregar paletas de colores específicas, títulos, entre otras características, que ayudarán a mejorar la visualización.

Son tantas las opciones que con seguridad te podrás divertir experimentando poco a poco con las diferentes alternativas disponibles. Hacer buenas visualizaciones no es tarea fácil y siempre implicará probar muchas opciones de capas, incluyendo la geometría.

Como se definió en la Sección 2.1, la capa de Geometría indica el tipo de visualización que se construirá. La selección de la geometría adecuada es tal vez la decisión más importante para obtener una visualización poderosa. Para escoger la capa de Geometría debemos preguntarnos qué queremos mostrar con ella (ver por ejemplo Abela (2008) o Alonso & González (2012)). En la Figura 2.12 se presenta un diagrama que te puede ayudar para decidir que tipo de gráfico (capa de Geometría) emplear según la intención y la clase de variable que se tenga.

Figura 2.12: Tipos de gráficos más comunes según lo que se desea comunicar y la clase de variable

Fuente: Adaptación de Alonso y González (2012).

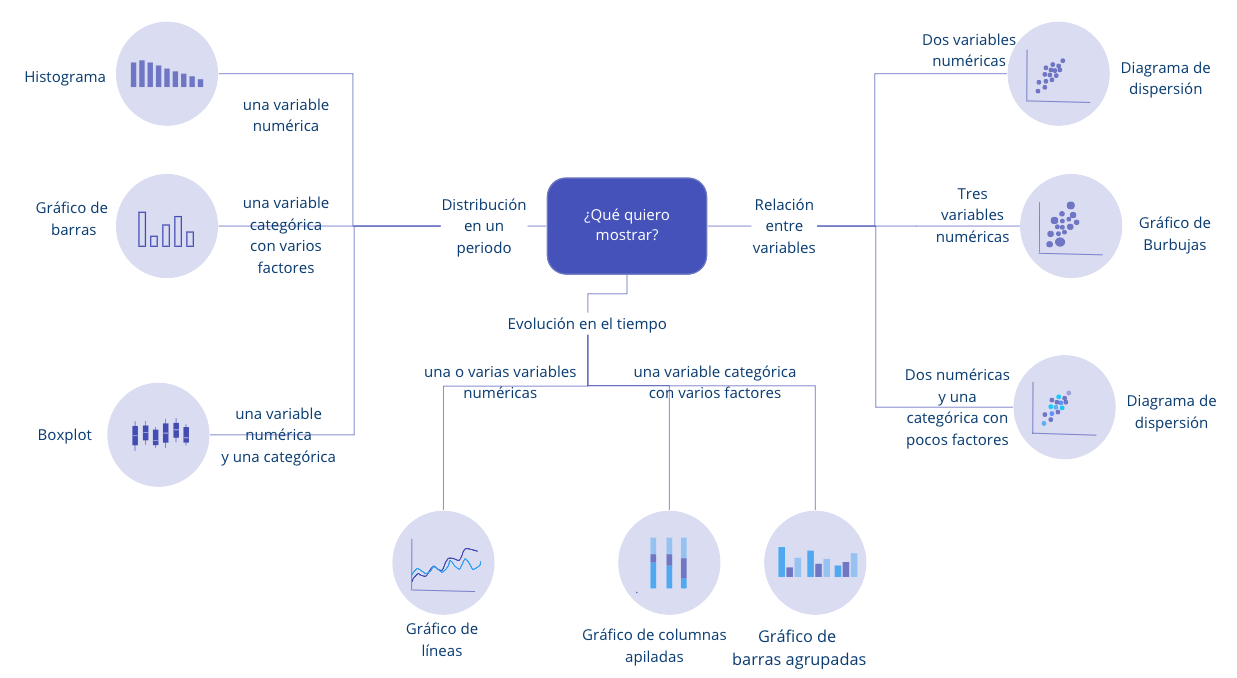
En el Capítulo 3 discutiremos los gráficos más empleados para mostrar la distribución de los datos (ver Figura 2.12). En el Capítulo 4 las visualizaciones más empleadas para mostrar la evolución de una variable (ver Figura 2.12) y en el Capítulo 5 aquellas para mostrar relaciones entre variables.

Referencias

Abela, A. (2008). ADVANCED PRESENTATIONS BY DESIGN. Pfeiffer.

Alonso, J. C. (2022). Empezando a transformar bases de datos con r y dplyr. http://www.icesi.edu.co/editorial/empezando-transformar/

Alonso, J. C., & González, A. (2012). Ggplot: Gráficos de alta calidad. Apuntes de Economía, 33, 29. https://www.researchgate.net/publication/323202960_Ggplot_graficos_de_alta_calidad

Alonso, J. C., & Ocampo, M. P. (2022). Empezando a usaR: Una guía paso a paso. http://www.icesi.edu.co/editorial/empezando-usar/

Bryan, J. (2017). Gapminder: Data from gapminder. https://CRAN.R-project.org/package=gapminder

Wickham, H. (2016). ggplot2: Elegant graphics for data analysis. Springer-Verlag New York. https://ggplot2.tidyverse.org

Wilkinson, L. (2012). The grammar of graphics. In Handbook of computational statistics (pp. 375–414). Springer.

En otras palabras, las lineas horizontales y verticales al interior de la visualización. A estas líneas también se les conoce como retícula (en inglés grid lines).↩︎
En el Capítulo 5 de Alonso & Ocampo (2022) puedes encontrar una introducción a esta clase de objetos.↩︎
En el Capítulo 1 de Alonso (2022) se presenta una breve introducción a esta clase de objetos.↩︎
El Capítulo 7 de Alonso & Ocampo (2022) presenta una breve introducción a los paquetes en R.↩︎
Si se emplea el operador %>% este argumento se puede pasar desde la línea anterior.↩︎
Virgulilla es el “palito curvo” que se emplea en el español encima de la letra ene (n) para convertirla en eñe (ñ). En inglés este operador (~) se conoce como tilde. Este operador se emplea en la base de R para definir la relación entre la variable dependiente y las variables independientes en la fórmula de un modelo estadístico. La variable a la izquierda del operador ~ es la variable dependiente y la o las variables a la derecha de éste son las variables independientes. Siguiendo esa tradición, en ggplot2 se emplea ~ para determinar que la capa de Facets dependerá de una variable x. Es decir, ~ x. ↩︎
Estas capas que no son pilares de la visualización se pueden adicionar en cualquier orden, pero en algunas ocasiones el resultado puede cambiar. En un momento te darás cuenta que por razones pedagógicas cambiamos el orden que se presentó inicialmente en el la Figura 2.2. ↩︎
Por ejemplo, están las funciones scale_y_continuous() y , scale_y_reverse(), que permiten convertir la escala del eje vertical (y) a una variable continua y cambiar a un orden descendente los valores del eje, respectivamente. ¡Intenta jugar con todas estas funciones! ↩︎
Esta función permite asignar límites para en los ejes para los que se presentará los datos. Esto genera un zoom en una parte de los datos. Intenta adicionar al código que generó la Figura 2.7 la siguiente línea de código coord\_cartesian(ylim = c(40,60)). Recuerda añadir el signo + antes de incluir esta nueva capa. Esto genera una visualización con solo los datos que están entre los límites. La diferencia entre expresar los límites de los ejes en la capa de Coordenadas y de Escalas, es que en el segundo caso los datos que estén por fuera se omiten y no se tienen en cuenta para ningún cálculo, mientras que en el segundo caso solo no se visualizan. Esto tiene un impacto sobre la visualización en especial cuando se adicione la capa de Estadística como se mostrará en el siguiente pie de página. ↩︎
Es interesante ver el efecto que tiene cambiar los límites de los ejes en la capa de Escalas o en la de Coordenadas. Adiciona primero al código que generó la Figura 2.8 una nueva línea modificando la capa de Coordenadas (recuerda adicionar el signo + al final de la línea anterios): coord\_cartesian(ylim = c(40,60)). Esto muestra exacatmane las mismas líneas de regresión de la Figura 2.8, pero haciendo un acercamiento a los datos que presentan una expectativa de vida al nacer entre 40 y 60 años. Ahora en vez de modificar la capa de Coordenadas, modifiquemos la de Escalas incluyendo el siguiente código: ylim(40,60). En esta oportunidad la línea de regresión para cada continente se calculó incluyendo solo los datos con una esperanza de vida al nacer entre 40 y 60. Ahí está la diferencia de emplear una de las dos capas para definir el límite de los datos. Todo dependerá de lo que quieras comunicar con tu visualización. ↩︎